 集合と位相
集合と位相 局所連結とは~定義・具体例・性質~
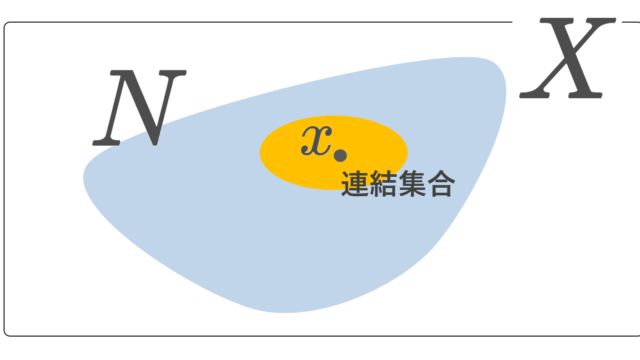
位相空間における局所連結とは,各点が連結な基本近傍系をもつことをいいます。連結であっても局所連結とは限らないし,局所連結であっても連結とは限りません。局所連結の定義・具体例・性質を述べましょう。最後には,点ごとの局所連結・弱局所連結についても解説します。
 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 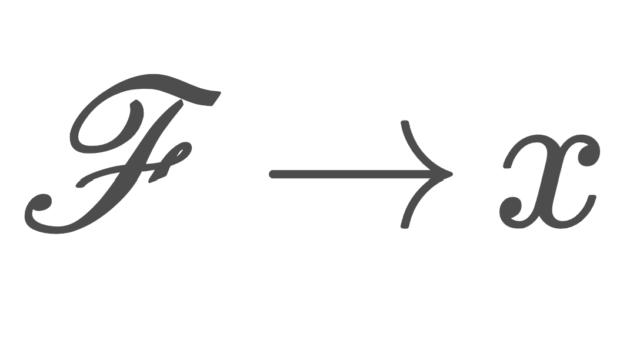 集合と位相
集合と位相 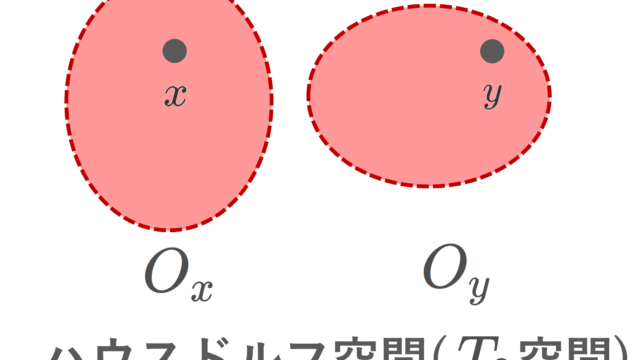 集合と位相
集合と位相