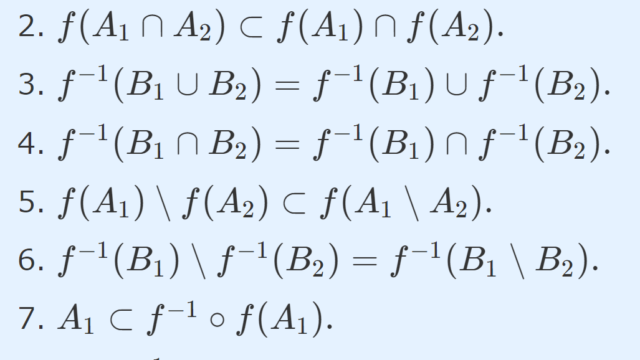集合と位相写像の像・逆像と集合との演算証明
像・逆像と集合との演算とその証明をします。f(A_1 \cup A_2) = f(A_1) \cup f(A_2), f(A_1 \cap A_2) \subset f(A_1) \cap f(A_2), f^{-1} (B_1 \cup B_2) = f^{-1} (B_1) \cup f^{-1}(B_2), f^{-1} (B_1 \cap B_2) = f^{-1} (B_1) \cap f^{-1}(B_2)
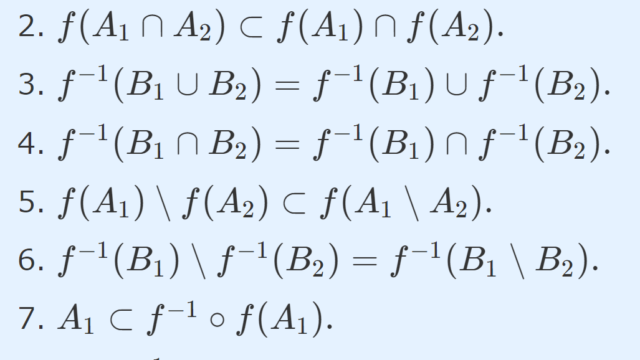集合と位相
集合と位相
微分積分学(大学)中間値の定理とは～主張・証明と何が本質なのかを解説～
中間値の定理とは，「連続関数なら，間の値を全て取る」という一見当たり前の定理です。これについて，その主張と，その証明を紹介します。さらに，根底にある「当たり前の性質」が何なのかも考えましょう。最後に位相空間論の言葉を用いた主張も述べます。
微分積分学(大学)ボルツァノ–ワイエルシュトラスの定理とその証明
大学教養数学のさまざまなところに登場する，ボルツァノ–ワイエルシュトラスの定理 (Bolzano–Weierstrass Theorem) について紹介します。まず1次元の場合を紹介し，次に多次元の場合を紹介して，最後に位相空間論の言葉を用いて述べます。
集合と位相距離空間の定義と6つの具体例～ユークリッド・マンハッタン距離～
距離空間 (metric space) とは，距離の構造にあたる距離関数 (distance function) を備えた集合のことです。そんな距離空間について確認し，ユークリッド距離やマンハッタン距離などを含む5つの具体例について確認していきましょう。
微分積分学(大学)【ディニの定理】各点収束から一様収束が従う定理とその証明
連続関数の列が単調増加に連続関数へ各点収束するとき，一様収束が言える「ディニの定理 (Dini's theorem) 」と呼ばれる定理があります。本記事ではこの定理の紹介とポイント解説，最後に証明を行います。証明のみ位相空間論の知識が必要です。
微分積分学(大学)アスコリ–アルツェラの定理とその証明～注意点を添えて～
アスコリ–アルツェラの定理（Ascoli–Arzelà theorem）は，解析学でよく使われる定理の一つですが，用語が難しく，適用条件にも注意が必要です。まず必要な用語として，「一様有界性」と「同程度連続性」の定義をし，定理を紹介します。