 本・サイトの紹介
本・サイトの紹介 位相空間論におけるオススメの本・参考書9選
大学数学における位相空間論を勉強するにあたって,おすすめの書籍や参考書を紹介します。
 本・サイトの紹介
本・サイトの紹介  本・サイトの紹介
本・サイトの紹介  本・サイトの紹介
本・サイトの紹介  本・サイトの紹介
本・サイトの紹介 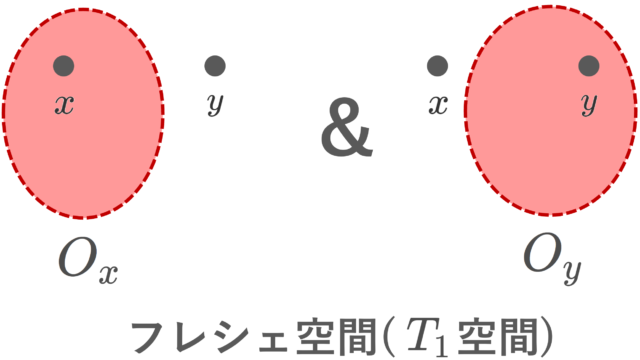 集合と位相
集合と位相 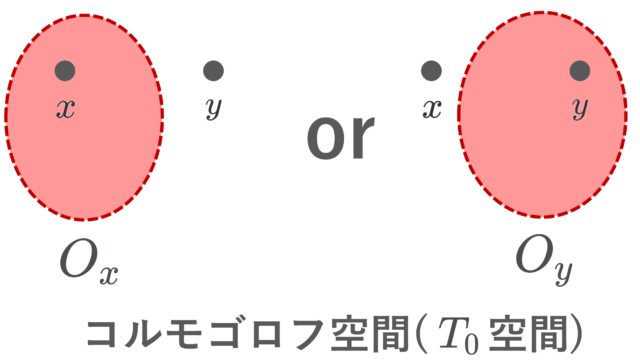 集合と位相
集合と位相 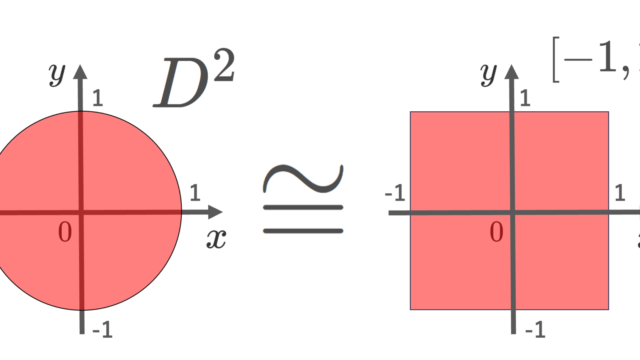 集合と位相
集合と位相 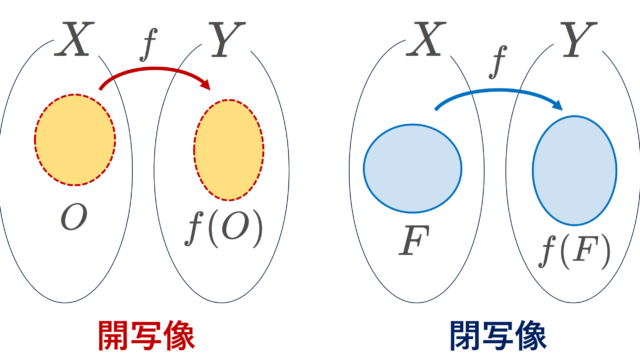 集合と位相
集合と位相 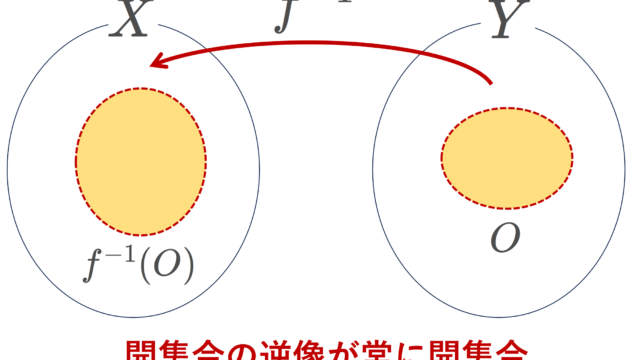 集合と位相
集合と位相 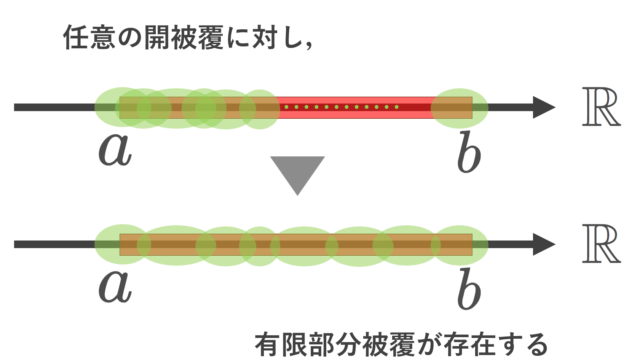 集合と位相
集合と位相