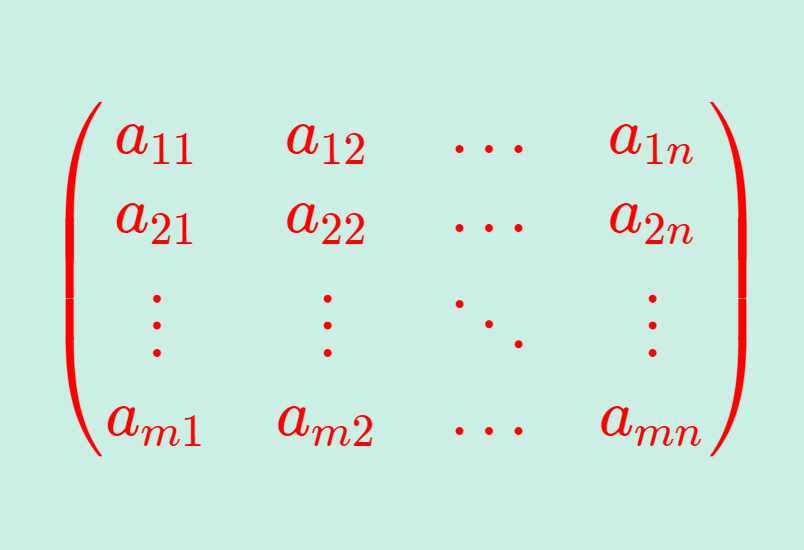ラグランジュの未定乗数法 (Lagrange multiplier) は,多変数関数における,条件つき極値問題を解く方法を指します。これについて,その内容とイメージ,証明を解説しましょう。
ラグランジュの未定乗数法
単に滑らかな関数 f(x,y) を最大化したいとしましょう。もし,何も制約がないなら,最大となる点は(広い意味で)極値になっているはずですから,
\frac{\partial f}{\partial x}=\frac{\partial f}{\partial y}=0
が成り立っているはずです,一方で, (x,y) は g(x,y)=0 をみたすという制約がついていたらどうでしょうか。
このような,制約付きの極値問題を解く方法が,ラグランジュの未定乗数法 (Lagrange multiplier) です。定理を述べましょう。
定理(ラグランジュの未定乗数法)
f(x,y), g(x,y) を C^1 級関数とし, g(x,y)=0 の下で, f(x,y) が極値を取る点を考える。そのような点 (x,y) は
\color{red} L(x,y,\lambda)=f(x,y)-\lambda g(x,y)
とおくと,\color{red} \dfrac{\partial g}{\partial x}=\dfrac{\partial g}{\partial y}=0 をみたすか,
をみたす。
f(x,y) の条件付き極値問題が, L(x,y,\lambda) という関数の条件なし極値問題にすり替わっていますね。
ラグランジュの未定乗数法は,制約付き関数の最大値や最小値の候補を求めるのに用いられます。
ラグランジュの未定乗数法の意味
さて,ラグランジュの未定乗数法の意味を考えましょう。ここで,勾配ベクトル (gradient)
\begin{align*} \operatorname{grad} f &= \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right),\\ \operatorname{grad} g&= \left(\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y} \right) \end{align*}
を用いると, \dfrac{\partial g}{\partial x}=\dfrac{\partial g}{\partial y}=0 は, \color{red}\operatorname{grad} g=\boldsymbol{0} を意味し, \dfrac{\partial L}{\partial x}=\dfrac{\partial L}{\partial y}=0 は, \color{red} \operatorname{grad} f = \lambda \operatorname{grad} g を意味します。
\dfrac{\partial L}{\partial \lambda}=0 は単に制約条件 g(x,y)=0 を指しているだけですから,これは無視すると,定理は以下のように言い換えることが可能です。
f(x,y), g(x,y) を C^1 級関数とし, g(x,y)=0 の下で, f(x,y) が極値を取る点を考える。そのような点 (x,y) は
\color{red}\operatorname{grad} g=\boldsymbol{0} をみたすか,ある \lambda が存在して,
\color{red} \operatorname{grad} f = \lambda \operatorname{grad} g
をみたす。
\operatorname{grad} g=\boldsymbol{0} または \operatorname{grad} f = \lambda \operatorname{grad} g とは, \operatorname{grad} f と \operatorname{grad} g の片方が \boldsymbol{0} または平行という意味になります。
ここで,勾配ベクトルは関数の最大傾斜方向を表し,等高線と垂直になるのでした。
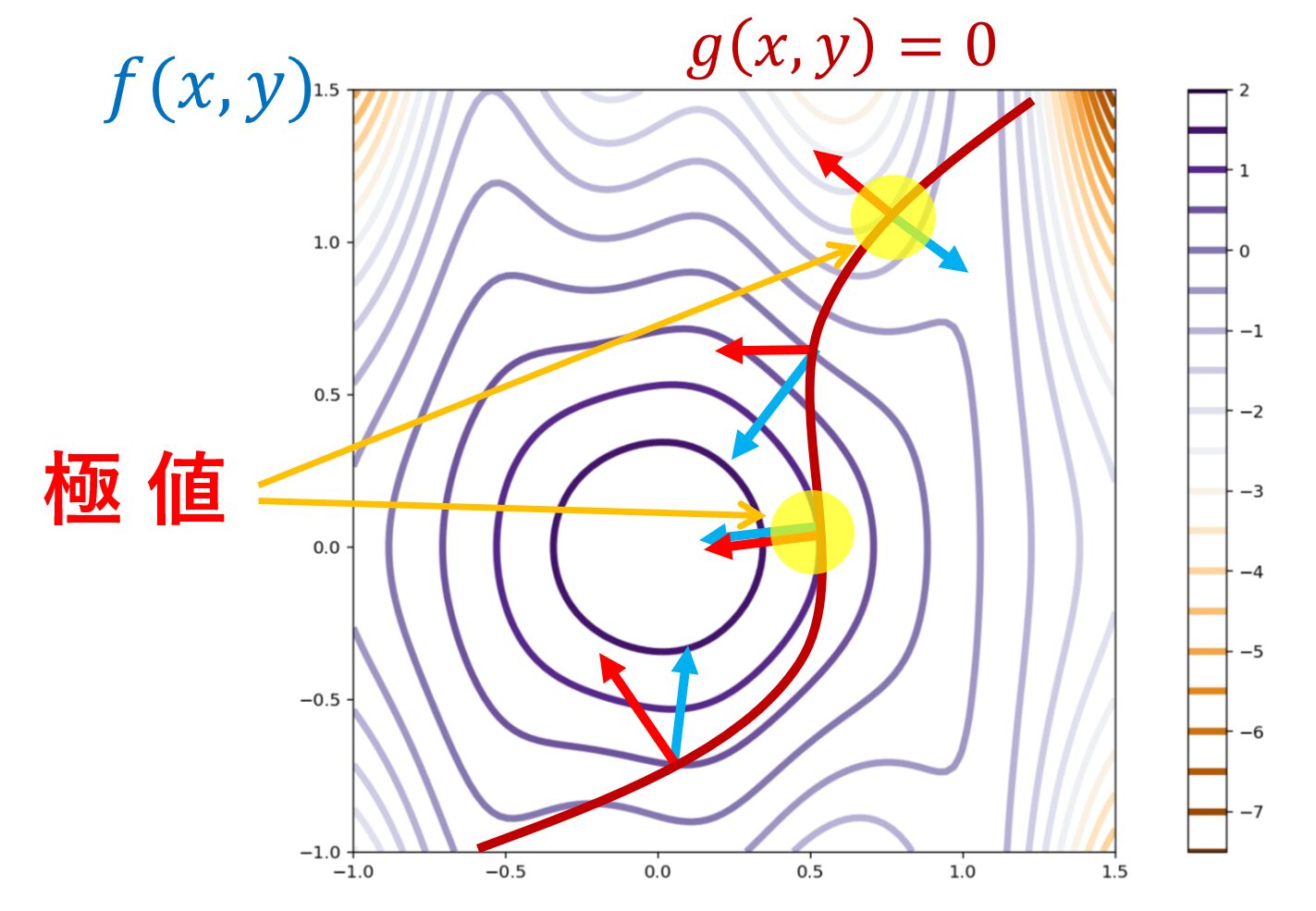
従って, \operatorname{grad} f と \operatorname{grad} g の片方が \boldsymbol{0} または平行という状態を等高線図を用いて表すと,以下のようになります。
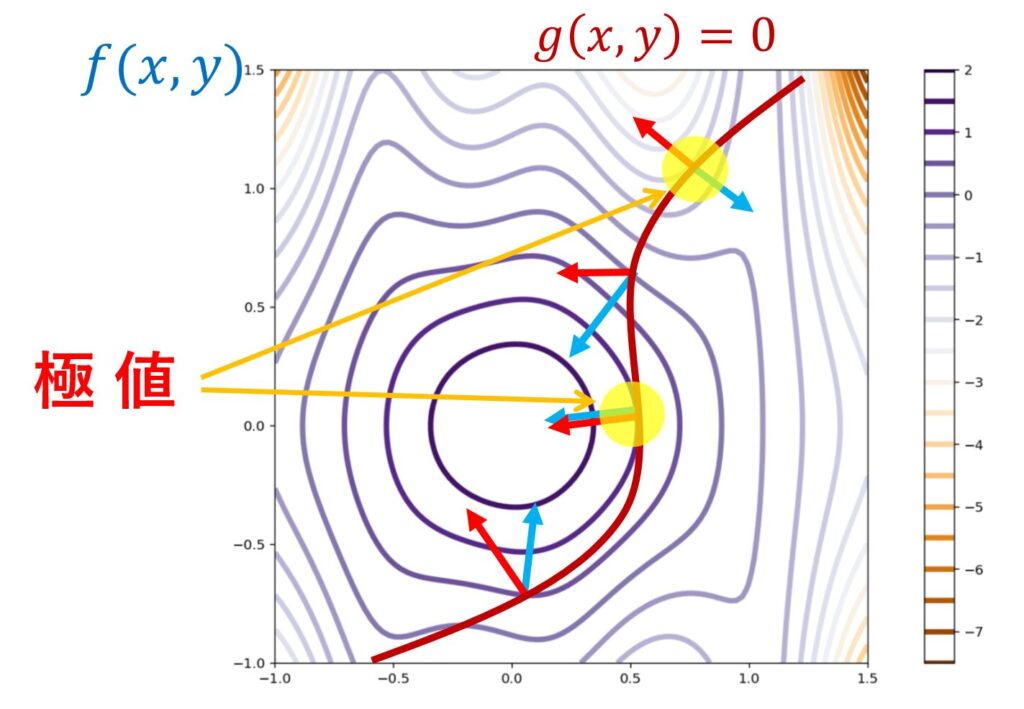
青の矢印は \operatorname{grad} f を,赤の矢印は \operatorname{grad} g を指しています。これらが平行のとき,ちょうど2つの等高線が接しており,極値(上の図の場合「最大値」)になっているのが,分かるのではないでしょうか。感覚的にはこんな感じです。
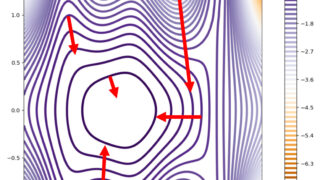
注意ですが,求めているのは極値の候補であり,必ずしも極値になるとは限りません。以下の図がその例です。
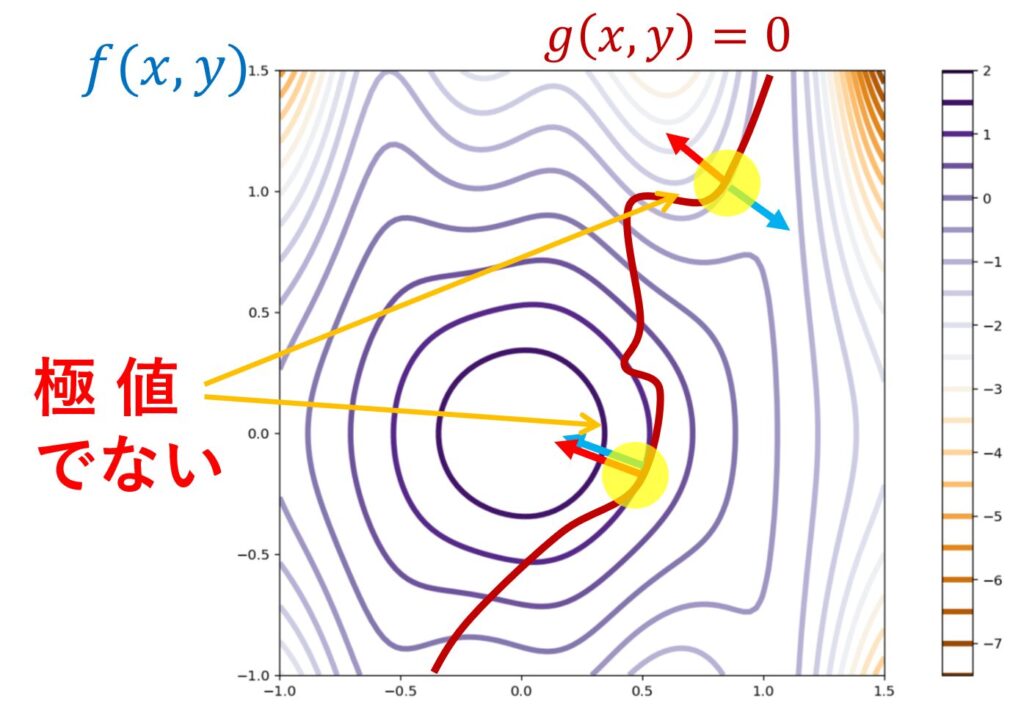
ラグランジュの未定乗数法の証明
簡単に,定理の証明をしておきましょう。
証明
(x_0,y_0) を極値とする。この点で, \dfrac{\partial g}{\partial x}=\dfrac{\partial g}{\partial y}=0 でないと仮定する。特に g_y\ne 0 としよう。陰関数定理より, (x_0,y_0) のまわりで g(x,y)=0 をみたす y は C^1 級関数 y=y(x) として表せ, y'=-g_x/g_y となる。
h(x)=f(x,y(x)) は (x_0, y_0) で極値を取るから,この点で
0=h' = f_x + f_y y'= f_x - f_y g_x/g_y
となる。よって, f_xg_y-f_yg_x=0 なので, \lambda = f_y/g_y とおくことで結論を得る。
証明終
より一般のラグランジュの未定乗数法
より文字が多く,制約も多い「ラグランジュの未定乗数法」の主張を述べておきましょう。
定理(ラグランジュの未定乗数法)
d 変数関数 f,g_1,\dots g_mは全て C^1 級とする。
g_1(x_1,\dots, x_d)=\dots = g_m(x_1,\dots,x_d)=0 の下で, f(x_1,\dots, x_d) が極値を取る点を考える。そのような点 (x_1,\dots, x_d) は
\color{red}\begin{aligned}& L(x_1,\dots, x_d,\lambda_1,\dots,\lambda_m)\\ &=f(x_1,\dots x_d)-\sum_{j=1}^m \lambda_j g_j(x_1,\dots, x_d)\end{aligned}
とおくと,\color{red}\displaystyle \sum_{j=1}^m \lambda_j \dfrac{\partial g_j}{\partial x_1}=\cdots = \sum_{j=1}^m \lambda_j \dfrac{\partial g_j}{\partial x_d}=0 をみたすか,
をみたす。
一つ目の条件 \displaystyle \sum_{j=1}^m \lambda_j \dfrac{\partial g_j}{\partial x_1}=\cdots = \sum_{j=1}^m \lambda_j \dfrac{\partial g_j}{\partial x_d}=0 は,言い換えると,
\operatorname{rank}\begin{pmatrix} \dfrac{\partial g_1}{\partial x_1} & \dots & \dfrac{\partial g_1}{\partial x_d}\\ \vdots & \ddots & \vdots \\ \dfrac{\partial g_m}{\partial x_1} & \dots & \dfrac{\partial g_m}{\partial x_d} \end{pmatrix} < m
を意味します。 \operatorname{rank} の中身はヤコビ行列です。