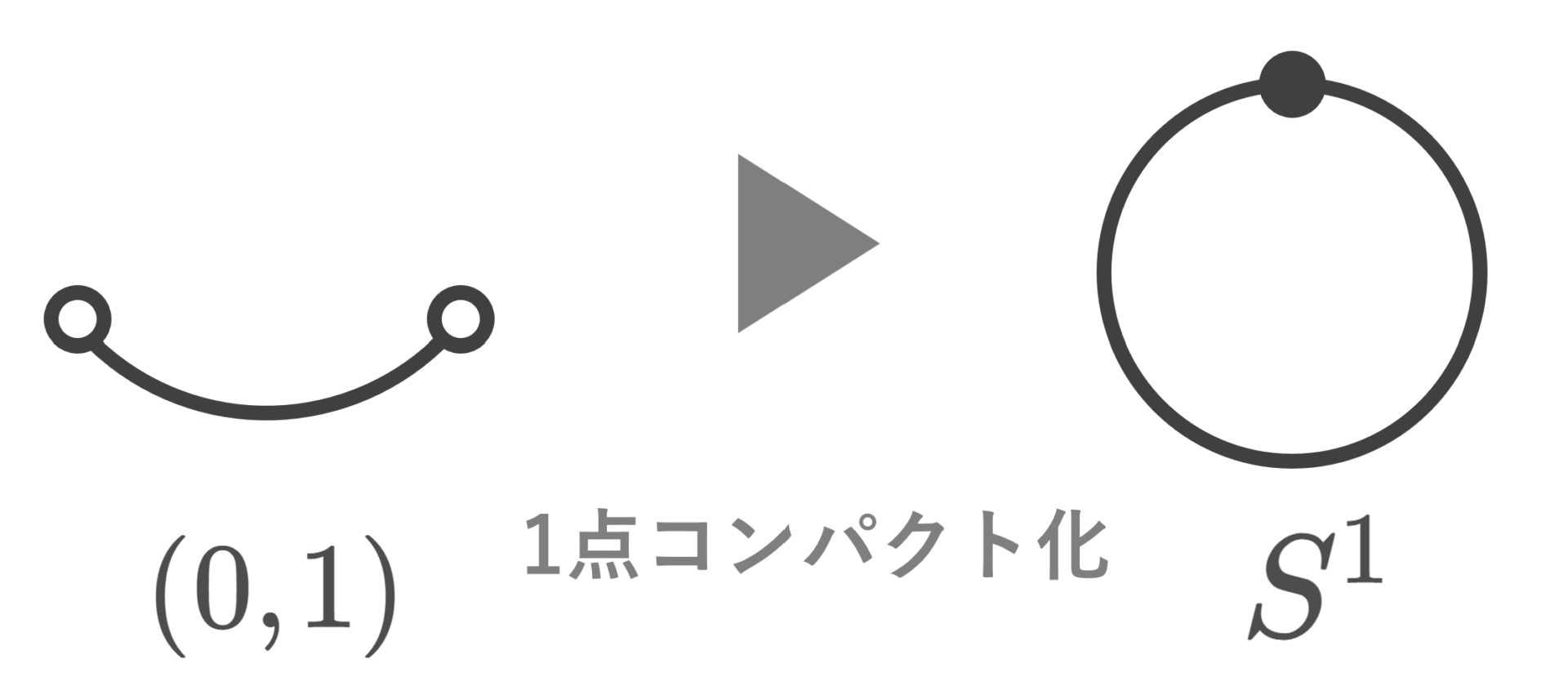
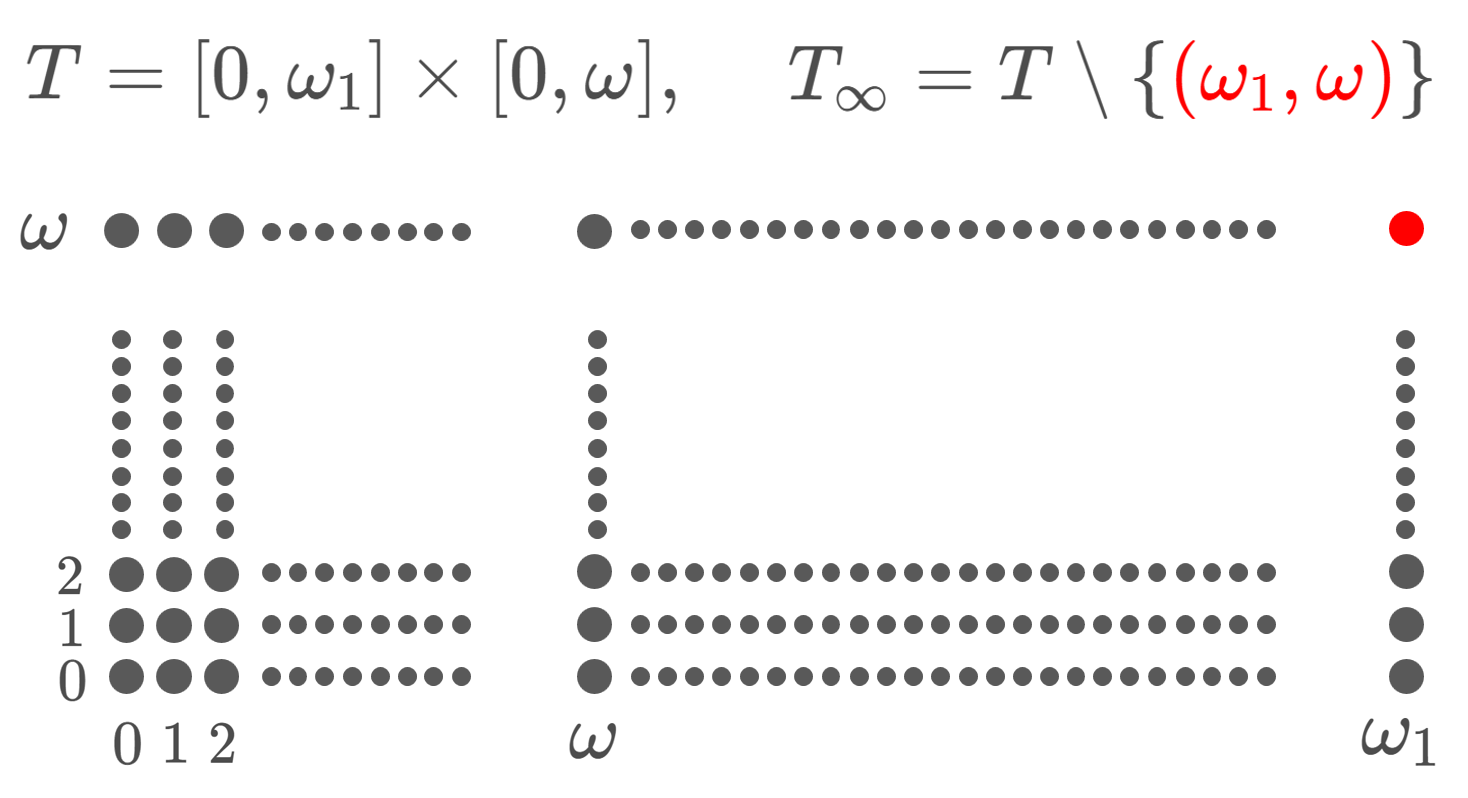アレクサンドロフの1点コンパクト化とは,位相空間に新たに1点を追加し,元の空間をそこに埋め込むことで,元の位相的構造を保ったままコンパクトにしようという手続きです。コンパクトな空間は性質が良く,扱いやすいですから,コンパクトにしたいという思いは自然です。
アレクサンドロフの1点コンパクト化について具体例も交えて詳しく紹介しましょう。
アレクサンドロフの1点コンパクト化
まずはコンパクト化が何かを定義し,それから1点のみを追加して位相空間をコンパクトにする方法を述べましょう。
コンパクト化とは
定義1(コンパクト化)
(X,\mathcal{O}) をコンパクトでない位相空間とする。このとき,コンパクトな位相空間 (K, \mathcal{O}') があって,
の両方が成り立つとき,K を X のコンパクト化 (compactification) という。
ふつうは, X と i(X) を同一視して, X\subset K と考えます。
なお, K がさらにコンパクトハウスドルフ空間である場合に限定して,コンパクト化という言葉を使う流儀もあります。文献に注意してください。
コンパクト化の具体例を簡単に挙げておきましょう。
- [0,1] は (0,1) のコンパクト化である
- [0,2] は (0,1) のコンパクト化ではない
- [0,1] は (0,1)\cap \mathbb{Q} のコンパクト化である
- (0,1)\cong S^1\setminus \{(1,0)\} であり, S^1 は S^1\setminus \{(1,0)\} のコンパクト化であるから, S^1 は (0,1) のコンパクト化とも見れる
\cong は同相(位相同型)の意味です。上の1.と4.より, (0,1) のコンパクト化は一通りでないことが分かります。一般にコンパクト化は何通りもあります。
アレクサンドロフの1点コンパクト化
1点コンパクト化 (one-point compactification) とは,元の空間に1点のみを付け加えてコンパクト化する手法です。
コンパクトでない位相空間 (X,\mathcal{O}) に対し, X 上にない1点 x_\infty を付け加えた集合 X^*=X\cup \{x_\infty\} を考えます。 X^* が X のコンパクト化になるように, X に位相を入れたいです。位相の入れ方は一通りではなく,たとえば,
\mathcal{O}^*=\mathcal{O}\cup \{X^*\}
とすると, (X^*,\mathcal{O}^*) は X のコンパクト化になっています(このような \mathcal{O}^* を \mathcal{O} の開拡大位相 (open extension topology) といいます)。実際, X^* の開被覆には, X^* そのものが含まれていないといけませんから, X^* はコンパクトで,また \mathcal{O}^* においては,\overline{X}=X^* となっています。
上の (X^*,\mathcal{O}^*) は最小の1点コンパクト化になっています。 x_\infty の近傍が X^* のみしかないくらい位相が小さい(粗い・弱い)ので,実用性は少ないです。コンパクトという性質は,位相が小さい(粗い・弱い)方が成り立ちやすいので,むしろ逆に,最も位相が大きい(細かい・強い)1点コンパクト化に興味があります。それが,アレクサンドロフの1点コンパクト化です。
定義2(アレクサンドロフの1点コンパクト化)
(X,\mathcal{O}) をコンパクトでない位相空間とする。このとき,新たに1点 x_\infty (無限遠点ということがある)を付け加えた集合 \large \color{red} X^*=X\cup \{x_\infty\} に対して,
- U\in\mathcal{O}
- x_\infty \in U かつ X\setminus U が \mathcal{O} におけるコンパクト閉集合
のいずれかが成り立つ U\subset X^* 全体の集合を \mathcal{O}^*,すなわち
\color{red} \mathcal{O}^* =\mathcal{O}\cup \left\{U\middle| \begin{gathered} x_\infty\in U,\, X\setminus U\text{ is } \\ \mathcal{O}\text{-closed and compact} \end{gathered}\right\}
とすると, (X^*, \mathcal{O}^*) はコンパクトな位相空間となる。この空間を, X におけるアレクサンドロフの1点コンパクト化 (one-point compactification) という。
普通,単に「1点コンパクト化」といえば,アレクサンドロフの1点コンパクト化を指します。よって以降,本記事もそれに従います。また,アレクサンドロフ拡大 (Alexandroff extension) ということもあります。定義2の前に述べたとおり,1点を足してコンパクト化する方法は一通りではありません。
\mathcal{O}^* が位相になることは,コンパクト閉集合の有限個の和集合はコンパクト閉集合であること,またコンパクト閉集合の部分閉集合(特に,コンパクト閉集合の無限個の共通部分)はコンパクト閉集合であることからわかります。各自示してみてください。コンパクトであることは, X^* の開被覆を任意にとったときに,その中から x_\infty を含んでいるものを1つ取れば,その集合の補集合はコンパクトなので,有限部分被覆が取れることから従います。
なお, X がコンパクトであったとしても,同様に X^* を構成することは可能です。しかしこのとき,X は X^* において稠密にはならず,定義1をみたさなくなってしまいます。ただ離れた1点を付け加えただけになってしまうのです。ここでは考えないことにしましょう。
なお,定義2の2.で,「コンパクト閉集合」を単に「コンパクト集合」としてしまうと,コンパクト集合の共通部分がコンパクトとは限らないため,位相空間の性質3.をみたさなくなってしまいます。よって,\mathcal{O}^* が位相とは限らなくなってしまい,定義として不適切です。ただし, X がハウスドルフ空間ならば,ハウスドルフ空間におけるコンパクト集合は常に閉集合なので,単に「コンパクト集合」としても問題ありません。
アレクサンドロフの1点コンパクト化の具体例
以下で, X^* は, X のアレクサンドロフの1点コンパクト化とします。以下で, \cong は同相(位相同型)の意味です。
例1( [0,1) の1点コンパクト化).
[0,1)^* \cong [0,1]![[0,1)の1点コンパクト化が[0,1]になるイメージ](https://mathlandscape.com/wp-content/uploads/2026/02/one-pt-compactification1-1024x311.png)
[0,1)^*=[0,1)\cup \{x_\infty\}\cong [0,1] を示しましょう。
U\subset [0,1)^* が x_\infty の開近傍 \iff K=[0,1)\setminus U はコンパクト \iff [0,1] \setminus K が 1 を含む開近傍
なので, x_\infty \in[0,1)^* の開近傍と 1\in [0,1] の開近傍が対応しています。ゆえに, [0,1)^*\cong [0,1] です。
例2( \R の1点コンパクト化).
\R^*\cong (0,1)^*\cong S^1
ただし, S^1=\{(x,y)\in \R^2\mid x^2+y^2=1\} であり, \R^2 からの相対位相が入っているとする。
区間 (0,1)\cong S^1\setminus \{(0,1)\} (後者は (0,1)\in \R^2)であり,明らかに (S^1\setminus \{(0,1)\})^*\cong S^1 ですから,言えます。
\R\cong S^1\setminus \{(0,1)\} の同相写像を,以下のような対応で構成することもあります。
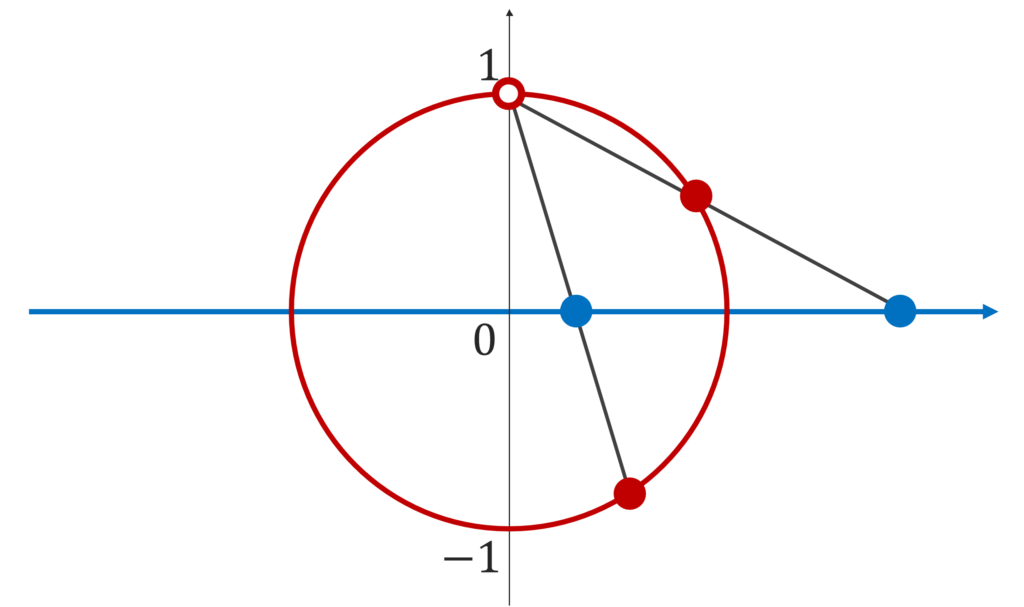
赤丸と青丸を対応させる写像は \R\cong S^1\setminus \{(0,1)\} を示す同相写像になります
例3( \R^2 の1点コンパクト化).
(\R^2)^* \cong \mathbb{C}^* \cong S^2
ただし, S^2=\{(x,y,z)\in \R^3\mid x^2+y^2+z^2=1\} であり, \R^3 からの相対位相が入っているとする。

\R^2\cong S^2\setminus \{(0,0,1)\} の同相写像を,以下のような対応で構成することもあります。
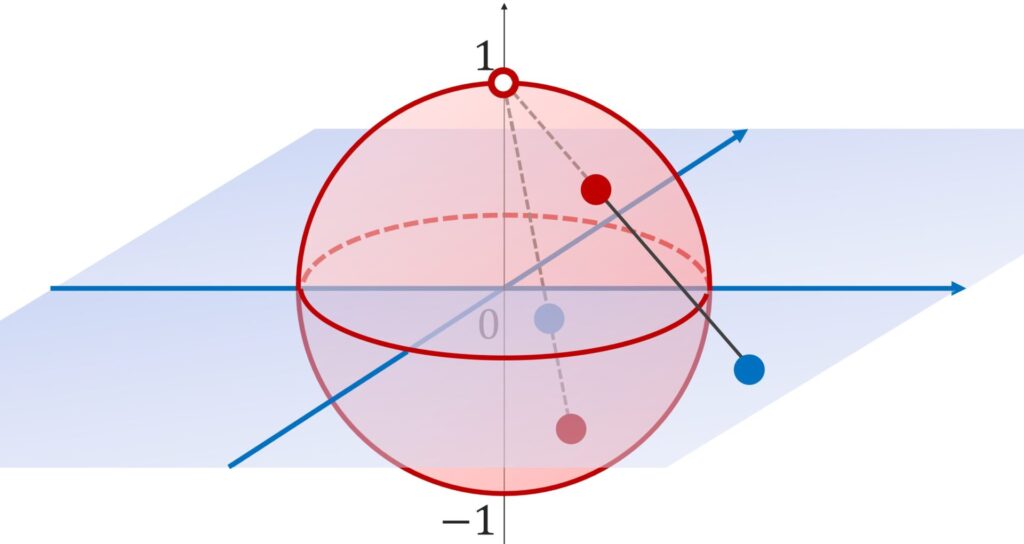
赤丸と青丸を対応させる写像は \R^2 \cong S^2\setminus \{(0,0,1)\} を示す同相写像になります
例4( \R^n の1点コンパクト化).
(\R^n)^*\cong S^n
ただし,S^n=\{ (x_1, \ldots, x_{n+1})\in \R^{n+1}\mid x_1^2+\cdots + x_{n+1}^2=1\} であり, \R^{n+1} からの相対位相が入っているとする。
理屈は例2.や例3.と同じです。
例5( \mathbb{N}, \mathbb{Z} の1点コンパクト化).
\mathbb{N}^*\cong [0,\omega]\cong \{0\}\cup \{1/n\mid n\in\mathbb{N}\}
ただし,\omega は最小の極限順序数として [0,\omega]=\{0,1,2,\ldots, \omega\} であり,また, \{0\}\cup \{1/n\mid n\in\mathbb{N}\} には \R からの相対位相が入っているとする。
また,\mathbb{Z}^*\cong \{0\}\cup \{1/n\mid n\in\mathbb{Z}\setminus \{0\}\} である。
\mathbb{N}^*=\mathbb{N}\cup \{x_\infty\} について, x_\infty の任意の開近傍は,補集合がコンパクトなので有限集合になります。 \{0\}\cup \{1/n\mid n\in\mathbb{N}\} についても, 0 の任意の開近傍は補集合が有限集合になります。 n\mapsto 1/n,\, x_\infty \mapsto 0 という写像が同相写像 \mathbb{N}^*\cong \{0\}\cup \{1/n\mid n\in\mathbb{N}\} になります。
例6(\mathbb{Q} の1点コンパクト化).
\mathbb{Q}^* はハウスドルフ( T_2)でない
後の定理で紹介しますが,\mathbb{Q} は局所コンパクト(任意の点がコンパクトな近傍をもつ)ではないため,そのコンパクト化はハウスドルフにはなりません。
例7(可算個の開区間の直和空間の1点コンパクト化).
\Bigl( \bigcup_{n=1}^\infty (2n, 2n+1) \Bigr)^* \cong \mathbb{H}
ただし,
はハワイアンイヤリングである(下図)。
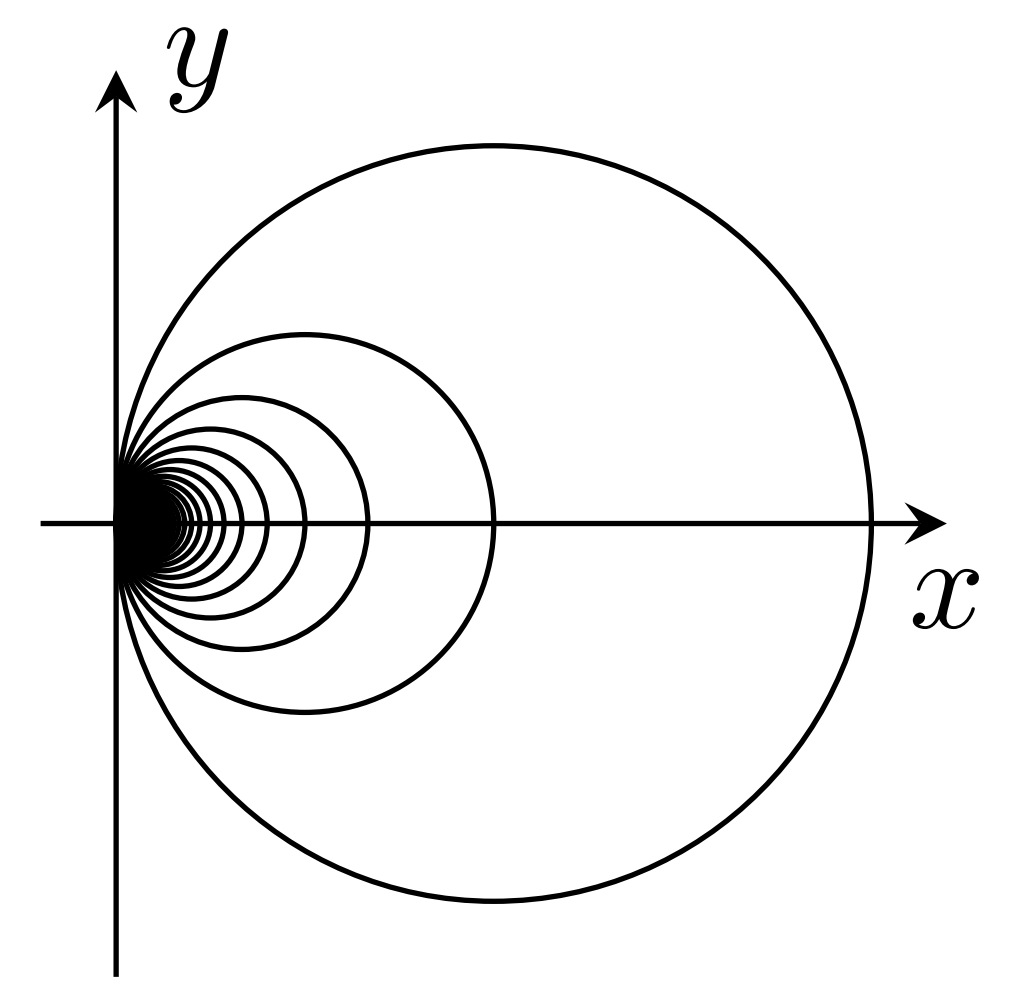
各開区間の1点コンパクト化は,例2.のように,端点をつなぎ合わせて S^1 になりますが,可算個の離れた開区間の1点コンパクト化は,可算個の S^1 で,つなぎ合わせる1点を共有する感じになります。ただし,単に以下のようなイメージではいけません。この図はコンパクトになっていません。
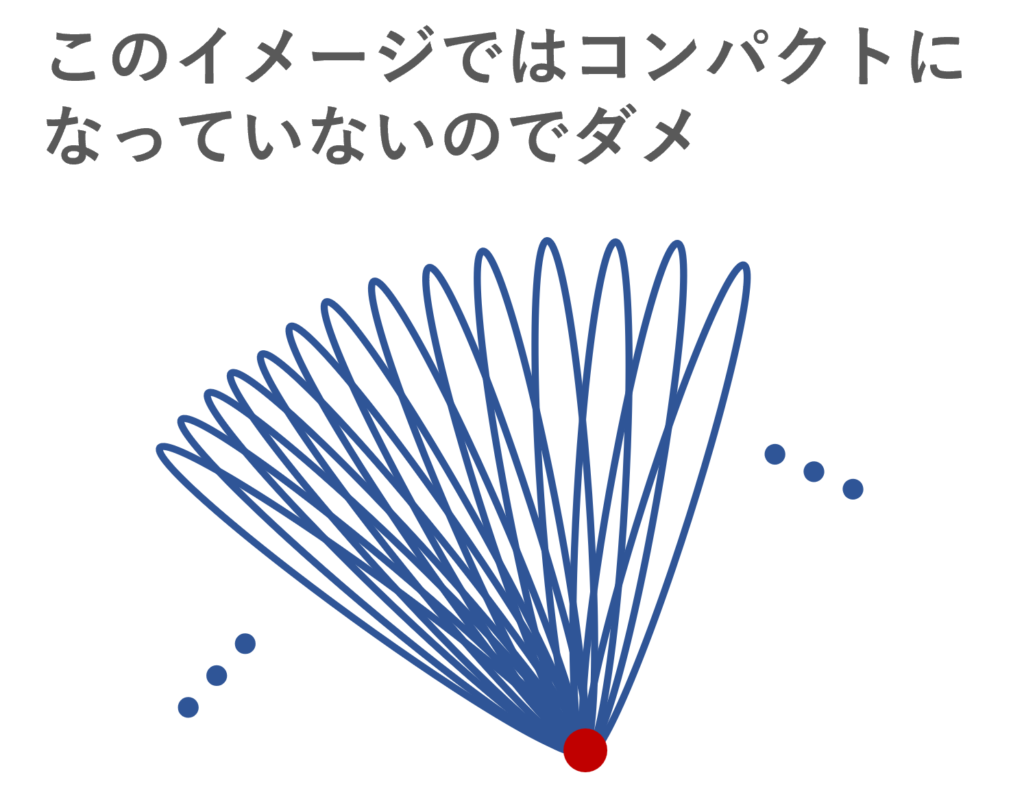
ハワイアンイヤリングのように入れ子の有界閉集合と解釈することで,コンパクトになっています。
アレクサンドロフの1点コンパクト化の性質
定理(1点コンパクト化の性質)
(X,\mathcal{O}) をコンパクトでない位相空間とし, X^* = X\cup \{x_\infty\},\, (X^*, \mathcal{O}^*) をアレクサンドロフの1点コンパクト化とする。
1.は特に,X^* がコンパクトハウスドルフ空間になる必要十分条件を述べています。コンパクトハウスドルフ空間は非常に扱いやすいですから,そうなるためには X がどうであればよいか,というのは非常に興味深い話なわけです。
証明
1.について
\implies について, X^* がハウスドルフであるとすると,X は X^* の開部分空間であるから,局所コンパクトハウスドルフである。
\impliedby について,異なる2点 x,y\in X が開集合で分離されることは良い。よって, x\in X と x_\infty が開集合で分離されることを示す。 X は局所コンパクトハウスドルフなので, \overline{V} がコンパクトな開近傍 x\in V\subset X が存在する。このとき, V, X^*\setminus \overline{V}\in\mathcal{O}^* であり,
x\in V,\, x_\infty\in X^*\setminus \overline{V} ,\, V\cap (X^*\setminus \overline{V}) =\emptyset
なので, x と x_\infty が開集合で分離できた。ゆえに, X^* はハウスドルフである。
2.について
T_1 であることは,1点集合が閉であることと同値であることに注意する。X は X^* の開部分空間であるから, \implies はよい。
\impliedby を示そう。X は X^* の開部分空間であるから, \{x_\infty\} は閉集合である。また, x\in X に対し, \{x\} は X におけるコンパクトで,かつ仮定より閉集合なので,\mathcal{O}^* の定義から, X^*\setminus \{x\}\in\mathcal{O}^* である。ゆえに, \{x\} は X^* における閉集合である。よって, X^* も T_1 である。
証明終