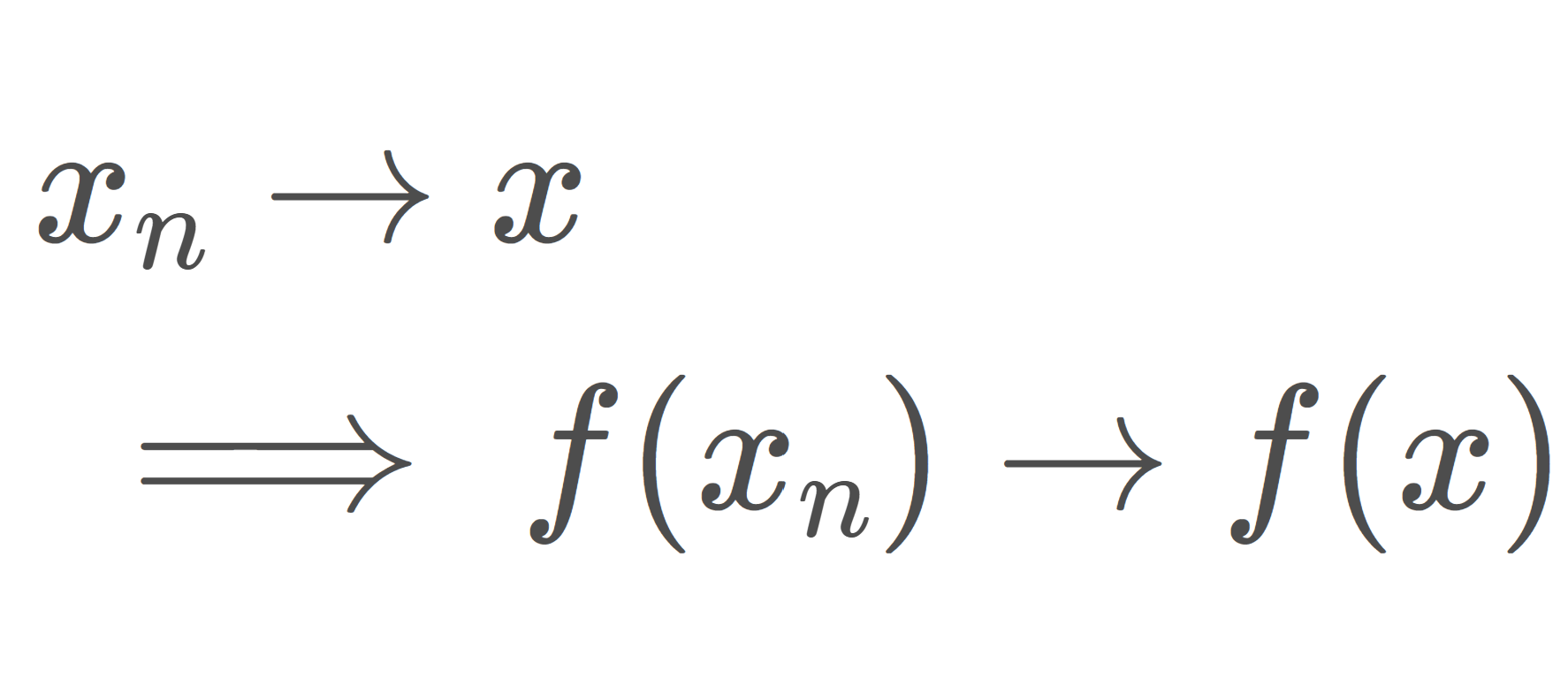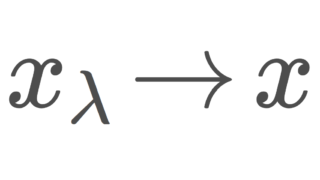写像 f が点列連続であるとは, x_n\to x ならば f(x_n)\to f(x) が成り立つことを言います。
点列連続性は,定義域が第一可算な空間であれば,連続性と同値ですが,一般には連続性より弱い概念です。このことを証明し,さらに一般には点列連続だが連続でない例があるので,それを紹介しましょう。
点列連続性の定義
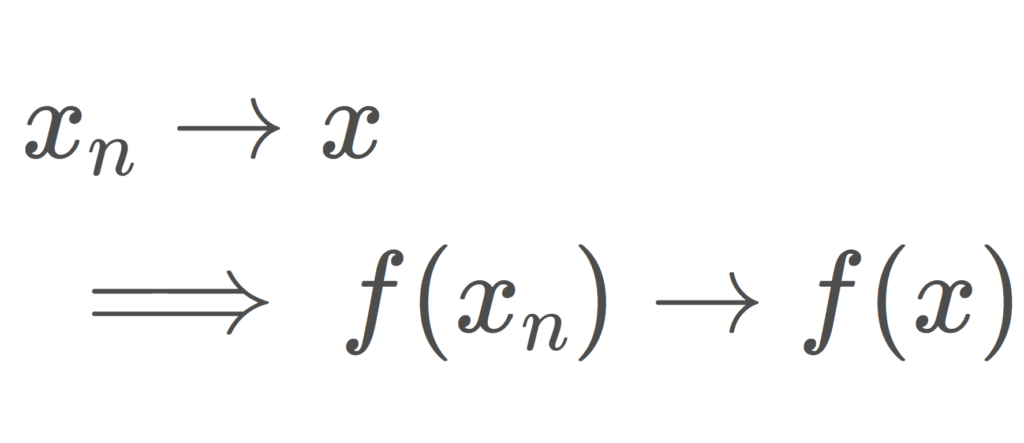
定義(点列連続)
X, Y を位相空間とし, f\colon X\to Y とする。
f が点 x\in X で点列連続 (sequentially continuous) であるとは, x_n\to x となる任意の点列 (x_n)\subset X に対して, f(x_n)\to f(x) となることである。
一般の位相空間における \color{red}\large x_n\to x とは, x の任意の近傍 U\subset X に対し,ある n_0\ge 1 が存在して,
n\ge n_0 \implies x_n\in U
が成り立つことを言います。
点列連続性と連続性を比較するにあたって,連続の定義を復習しておきましょう。ここでは「1点で連続」を考えています。
各点で連続であることや, f が連続写像であることについては,位相空間における連続写像の定義と性質を詳しくで詳しく解説しています。
ネット(有向点族)は,点列の概念を一般化したもので, x で連続であるということは,ネット(有向点族)を使って記述できます。ネット(有向点族)について詳しくは,以下で解説しています。
上記の連続の定義において,「ネット(有向点族)」を「点列」に変えたものが,点列連続の定義と言えます。
連続なら点列連続だが,逆は必ずしも成立しない
f\colon \R\to\R なら,ある点で連続であることと点列連続であることは同値であり,連続であることの証明に,点列連続性を示すことが頻繁にあります。しかし,一般の位相空間では,連続性と点列連続性の概念は一致せず,点列連続性の方が弱い概念になります。
定理(連続 ⇒ 点列連続)
X, Y を位相空間とし, f\colon X\to Y とする。このとき,
X が第一可算であれば,点列連続 ⇒ 連続も成立します。第一可算とは,各点で高々可算な基本近傍系をとれることを言います。たとえば, \R^n に通常の位相を入れたものは第一可算です。
点列はネット(有向点族)の一種なので,連続のネット(有向点族)による定義を認めると,1.の連続 ⇒ 点列連続は当たり前です。ただし,ここではネット(有向点族)の知識を仮定せずに証明しましょう。
証明
1.について
点列 (x_n) が, x_n\to x をみたすとする。f(x)\in V を, f(x) の任意の近傍とする。 f が x\in X で連続なので, f^{-1}(V)\subset X は x の近傍である。
よって,ある n_0 が存在して, n\ge n_0\implies x_n\in f^{-1}(V) となるが,これは n\ge n_0\implies f(x_n)\in V ということなので, f(x_n)\to f(x) である。
2.について
背理法で示す。 f が x\in X で連続でないと仮定する。このとき,ある f(x) の近傍 V が存在して, f^{-1}(V) が x の近傍でない。 X は第一可算なので,
U_1\supset U_2\supset U_3\supset \cdots
を x の基本近傍系とすると, 各 n\ge 1 で U_n\cap (f^{-1}(V))^c\ne\emptyset なので, x_n \in U_n\cap (f^{-1}(V))^c を取ってくることで, x_n \to x とできる。一方で, x_n\notin f^{-1}(V) から f(x_n)\notin V なので, f(x_n)\nrightarrow f(x) である。これは点列連続性に矛盾している。
証明終
点列連続だが連続でない例
上の定理より,点列連続性は連続性より弱い概念だということが分かりました。実際に,点列連続だが連続でない例を挙げましょう。第一可算なら両者の概念は同値になるので,今から挙げる例は当然第一可算ではありません。
例1(補可算位相から離散位相への恒等写像).
\mathcal{O}_c=\{\emptyset \}\cup \left\{O\subset X\middle|\begin{gathered} X\setminus O \text{ is at most} \\ \text{countable}\end{gathered}\right\}
を補可算位相,すなわち補集合が高々可算集合または X である部分集合を開集合系とする位相とする。このとき,\operatorname{id}(x)=x となる恒等写像 \operatorname{id}\colon (X,\mathcal{O}_c)\to (X, 2^X) は,連続ではないが点列連続である。
連続でないことは, \operatorname{id}^{-1}(U)=U であることから分かります。点列連続であることを示しましょう。 (x_n)\subset X を, x_n\to x in (X, \mathcal{O}_c) としましょう。このとき,
\bigl(X\setminus (x_n)\bigr) \cup \{x\}
も x の近傍であるはずで,これと x_n\to x であることから,ある n_0\ge 1 が存在して, n\ge n_0\implies x_n=x でなくてはならないです。すなわち,十分大きな n で (x_n) は x に一致する定数列です。よって,明らかに \operatorname{id}(x_n)\to \operatorname{id}(x) in (X, 2^X) ですね。
次の例2.を理解するには,順序位相の定義と順序数における順序位相の性質の理解が必要です。
例2(順序位相から0-1値関数).
\omega_1 を最小の非可算順序数とし,\omega_1+1= [0,\omega_1] には順序位相が入っているとする。また,\{0,1\} には離散位相入っているとする。このとき, f\colon [0,\omega_1]\to \{0,1\} を
f(x)= \begin{cases} 0 & x\in [0,\omega_1), \\ 1 & x=\omega_1\end{cases}
と定めると, f は連続ではないが点列連続である。
1点集合 f^{-1}(1)=\{\omega_1\} は開集合でないので,連続ではありません。一方で,点列 (x_n)\subset [0,\omega_1) が x_n\to x となるならば, x\in [0,\omega_1) となることが知られているため, f(x_n)\to f(x) です。
また,上の赤字の部分から, (x_n)\subset [0,\omega_1] が x_n\to \omega_1 となるならば,ある n_0\ge 1 が存在して,n\ge n_0\implies x_n=\omega_1 であることもわかるので,結局 f(x_n)\to f(x) です。ゆえに,点列連続であることが示せました。