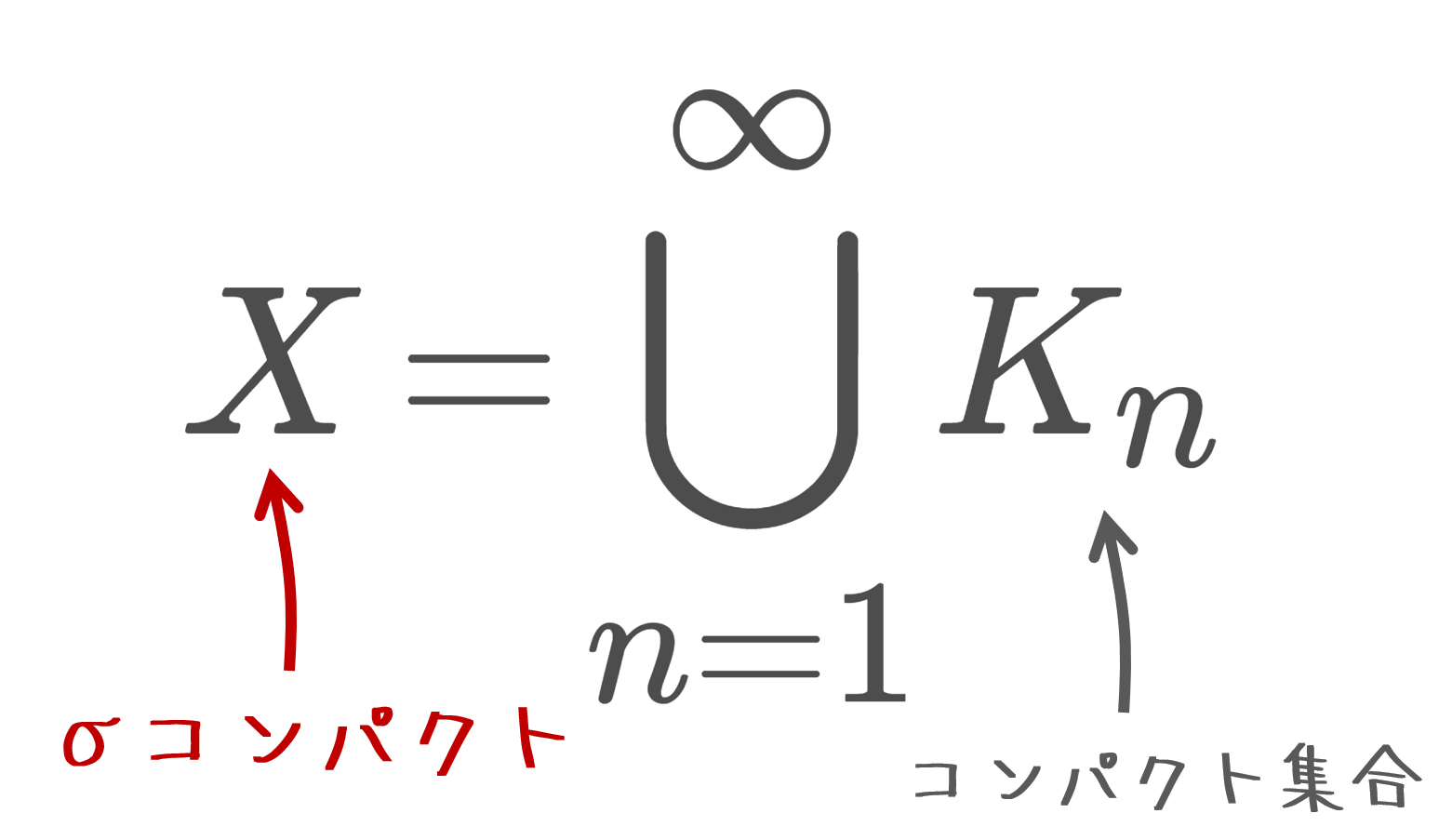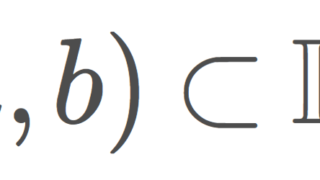σコンパクト空間 (シグマコンパクト空間; σ-compact space) とは,コンパクト部分集合の可算和でかけるような位相空間のことを言います。コンパクト性よりは弱いですが,ある程度扱いやすい空間です。
σコンパクト空間について,その定義と性質・具体例を詳しく紹介しましょう。
σコンパクト空間の定義
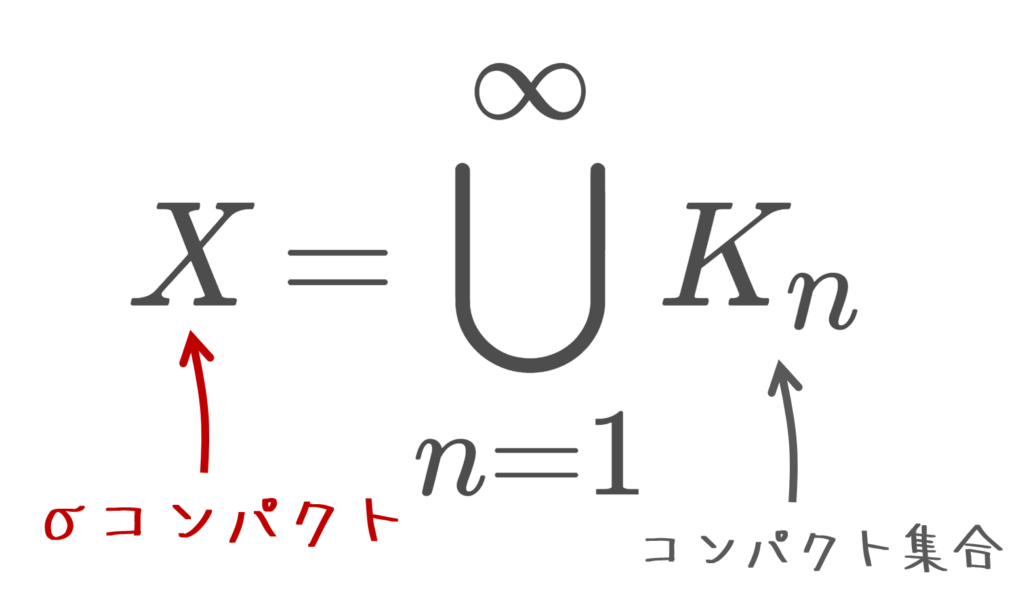
定義(σコンパクト)
(X,\mathcal{O}) を位相空間とする。 X がコンパクト集合の可算個の和集合でかけるとき, X はσコンパクト (シグマコンパクト; σ-compact) であるという。
すなわち, \{K_n\} をコンパクト集合の族として,
X= \bigcup_{n=1}^\infty K_n
とかける空間がσコンパクト空間です。明らかにコンパクト空間はσコンパクトです。また例えば, \R=\bigcup_{n=1}^\infty [-n, n] とかけるので, \R はσコンパクトです。
コンパクト性にまつわる様々な定義をまとめておきましょう。
| 名称 | 定義 |
|---|---|
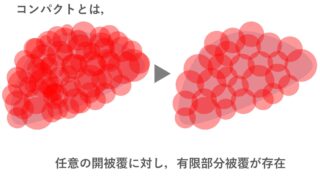
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| 強局所コンパクト (strongly locally compact) | 任意の点がコンパクトな閉近傍をもつ |
| 相対コンパクト (relatively compact) | 閉包がコンパクトな部分集合 |
| 可算コンパクト (countably compact) | 任意の可算開被覆が有限部分被覆をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 極限点コンパクト (limit point compact) | 任意の無限部分集合が集積点をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち,各点ごとに有限個の集合でしか覆われていない)開細分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち,各点ごとに有限個の集合でしか覆われていない近傍をもつような)開細分被覆をもつ |
σコンパクトの性質とその証明
定理(σコンパクトの性質)
リンデレーフ (Lindelöf) とは,『任意の開被覆が可算部分被覆をもつこと』でした。『』内において,「可算」の部分を「有限」に変えれば,コンパクトの定義になります。
1.は明らかですね。2.から4.を示しましょう。
2.から4.の証明
2.について
\{U_\lambda\}\subset \mathcal{O} を X の開被覆とする。 X はσコンパクトであるから,ある可算個のコンパクト集合の族 \{K_n\} が存在して,
X=\bigcup_{n=1}^\infty K_n
とあらわせる。 \{U_\lambda\} は各 K_n の開被覆にもなっており,各 K_n はコンパクトであるから,有限部分被覆 \{ U_{n,1}, U_{n,2},\ldots, U_{n, m_n}\}\subset\{U_\lambda\} が存在して, K_n \subset\bigcup_{k=1}^{m_n} U_{n,k} とできる。
であるから, X はリンデレーフである。
3.について
X は局所コンパクトなので,各点 x\in X に対し,コンパクトな近傍 K_x が存在する。 U_x=\operatorname{Int}(K_x) を K_x の内部(開核)とする。 x\in U_x なので, \{U_x\}_{x\in X} は X の開被覆である。
X はリンデレーフであるから,可算部分被覆 \{ U_{x_n}\}_n が存在する。このときの \{K_{x_n}\}_n は,コンパクトな可算被覆になっているので, X はσコンパクトである。
4.について,まず有限個の直積もσコンパクトであることを示す
X_j \; (1\le j\le n) をσコンパクト空間とすると,コンパクト集合 K_{j,1}, K_{j,2},\ldots \subset X_j が存在して,
X_j = \bigcup_{l=1}^\infty K_{j, l}
と表せる。このとき,
であり, K_{1,l_1}\times K_{2,l_2}\times\cdots \times K_{n, l_n} はコンパクト集合なので, \prod_{j=1}^n X_j はσコンパクトである。
次に,無限個の直積がσコンパクトとは限らない例を挙げる
\R^\mathbb{N}= \prod_{j=1}^\infty \R =\{ (x_j)\mid x_j\in \R\} を,実数列全体の集合とする。 \R はσコンパクトなので,これはσコンパクト空間の可算個の直積になっている。背理法で示す。もし, \R^\mathbb{N} がσコンパクトであるとすると,コンパクト集合の可算族 \{ K_n\}\subset \R^\mathbb{N} が存在して,
\begin{align} \R^\mathbb{N}= \bigcup_{n=1}^\infty K_n\end{align}
と表せる。 p_j \colon (x_j)\mapsto x_j を射影とする。射影は連続写像である。コンパクト集合の連続像はコンパクトであるから, p_j (K_n)\subset \R はコンパクトである。よって最大値 \max p_j(K_n) が存在する。このとき,数列
は,どの K_n にも入らないので, (1) 式に矛盾している。よって, \R^\mathbb{N} はσコンパクトではない。
証明終
無限個のコンパクト集合の直積は,チコノフの定理 (Tychonoff’s theorem) よりコンパクトですが,σコンパクト集合の無限個の直積はσコンパクトとは限らないわけです。
σコンパクト空間・そうでない空間の具体例
σコンパクトである例,そうでない例を紹介します。今回はσコンパクト・リンデレーフ・局所コンパクトを絡めながら,具体例を挙げていきます。以下の図は,これから紹介するどの具体例が,どの性質をみたしているのかを表した図です。

\R=\bigcup_{n=1}^\infty [-n, n] とかけるので, \R はσコンパクトです。
例2(有理数 \mathbb{Q}).
有理数全体の集合 \mathbb{Q} は通常の位相でコンパクトでも,局所コンパクトでもないが,可算集合なのでσコンパクトではある。ゆえに,リンデレーフでもある。
K\subset \mathbb{Q} をコンパクト集合とします。距離空間においては,コンパクトであることと点列コンパクトであることは同値なので,K は点列コンパクトです。すなわち,K 値の数列は,常に K 値に収束する部分列を持ちます。よって, K は \R における疎集合 (nowhere dense) でなければなりません。すなわち, K の \R における閉包の内部(開核)は空集合です。
一方で,各点 q\in \mathbb{Q} の近傍 U は,ある \varepsilon>0 が存在して, (q-\varepsilon, q+\varepsilon)\cap \mathbb{Q}\subset U となるため, U がコンパクトになることはあり得ません。よって, \mathbb{Q} が局所コンパクトではありません。
距離空間においては,可分性・第二可算・リンデレーフであることは同値になります(→第二可算公理と第二可算な位相空間の例・性質)。このことからも \mathbb{Q} がリンデレーフであることは分かります。
例3(無理数 \R\setminus\mathbb{Q}).
無理数全体の集合 \mathbb{P}=\R\setminus\mathbb{Q} は通常の位相でコンパクトでも,局所コンパクトでもない。σコンパクトでもない。しかし,リンデレーフではある。
局所コンパクトでないことは,例2.と同じ理由で分かります。また, K\subset \mathbb{P} がコンパクトならば,例2.と同じ理由で \R における疎集合 (nowhere dense) ですが,\mathbb{P} は第二類集合 (second category) すなわち, \R における疎集合の可算和でかけない集合であることが知られているため,σコンパクトとは言えません。
また, \{ \sqrt{2}+q\mid q\in\mathbb{Q}\} は \mathbb{P} における稠密な可算部分集合になっていることから, \mathbb{P} は可分です。距離空間においては,可分性・第二可算・リンデレーフであることは同値であるので,\mathbb{P} はリンデレーフです。
例5(離散位相).
(X,2^X) を離散空間とする。
1点集合は開集合かつコンパクトなので, X は局所コンパクトです。
ちなみに,明らかに X がコンパクトである必要十分条件は X が有限集合であることです。
例6(K位相).
K= \{ 1/n\mid n=1,2,3,\ldots\} とする。 \R の部分集合族
\mathcal{B}_K =\{ (a,b)\mid a<b\}\cup\{ (a,b)\setminus K \mid a<b \}
を開基とする位相 \mathcal{O}_K をK位相 (K-topology) またはスミルノフ位相 (Smirnov’s deleted sequence topology) という。
(\R, \mathcal{O}_K) はコンパクトでも局所コンパクトでもないが,σコンパクトである。よってリンデレーフでもある。
この空間では, [0,1] はコンパクトではありません。実際,開被覆
(\R \setminus K) \cup \bigcup_{n=1}^\infty \left( \frac{1}{2n}, \frac{3}{2n}\right)
は有限部分被覆を持ちません。また, [0,1]\setminus K も開被覆 \bigcup_{n=1}^\infty (1/(n+1),1/n ) が有限部分被覆をもたないため,コンパクトではないです。同じ理由で, 0 の近傍は常にコンパクトではないので, (\R, \mathcal{O}_K) は局所コンパクトでもありません。一方で,
より,σコンパクトは言えます。K位相のその他の性質ついては,以下で掘り下げています。
例7(補可算位相).
X を非可算集合とし,
\mathcal{O}_c=\{\emptyset \}\cup \left\{O\subset X\middle|\begin{gathered} X\setminus O \text{ is at most} \\ \text{countable}\end{gathered}\right\}
を,補集合が高々可算集合である部分集合全体(と \{\emptyset\} との和集合)とすると, (X,\mathcal{O}_c) は位相空間になる。この位相を補可算位相 (cocountable topology, countable complement topology) という。
(X,\mathcal{O}_c) はコンパクトでも局所コンパクトでもない。σコンパクトでもない。しかし,リンデレーフではある。
補可算位相については,以下で解説しています。
例8(ゾルゲンフライ直線).
実数全体の集合 \R に対し,
\mathcal{B}_l=\{ [a,b)\subset \R\mid a<b\}
を開基とする位相 \mathcal{O}_l を下限位相 (lower limit topology, right half-open interval topology) といい,位相空間 (\R, \mathcal{O}_l) をゾルゲンフライ直線 (Sorgenfrey line) という。
(\R,\mathcal{O}_l) はコンパクトでも局所コンパクトでもない。σコンパクトでもない。しかし,リンデレーフではある。
ゾルゲンフライ直線については,以下で解説しています。