 集合と位相
集合と位相 K位相(スミルノフ位相)の定義と性質とその証明
K位相(スミルノフ位相)とは,通常の実数の位相に,とある閉集合を加えた位相空間です。連結だが局所連結でない,メタコンパクトだがパラコンパクトでない等の性質をもちます。K位相(スミルノフ位相)について,その定義と性質をていねいにまとめましょう。
 集合と位相
集合と位相 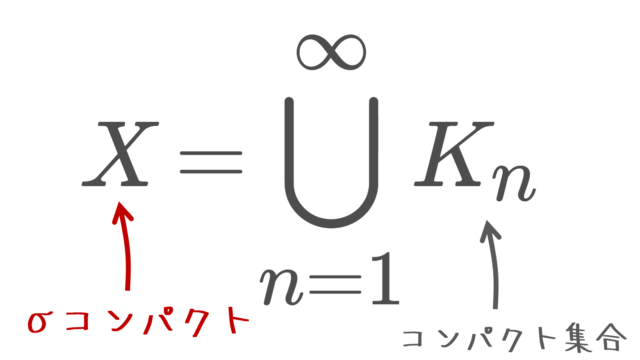 集合と位相
集合と位相 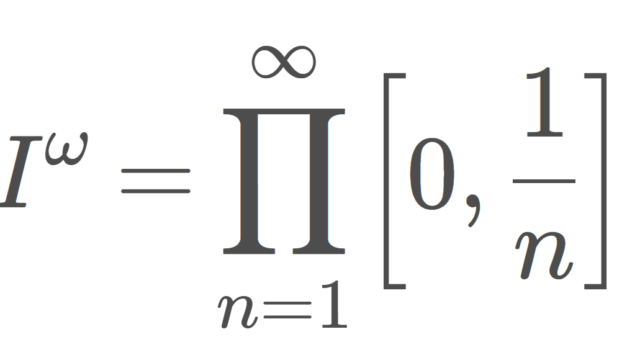 集合と位相
集合と位相  集合と位相
集合と位相 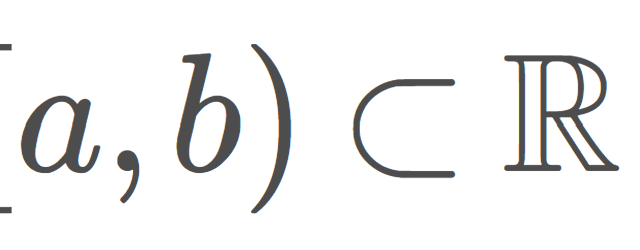 集合と位相
集合と位相 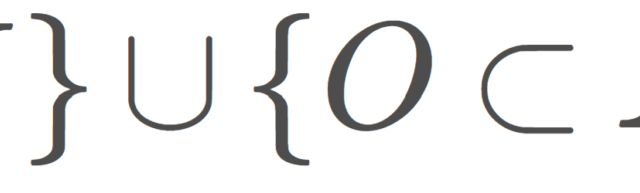 集合と位相
集合と位相 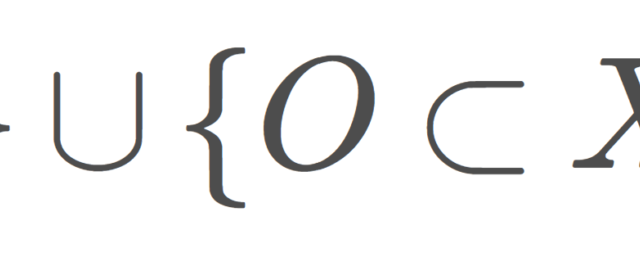 集合と位相
集合と位相 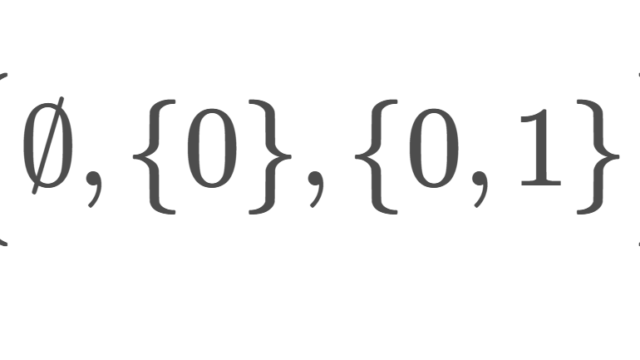 集合と位相
集合と位相  集合と位相
集合と位相 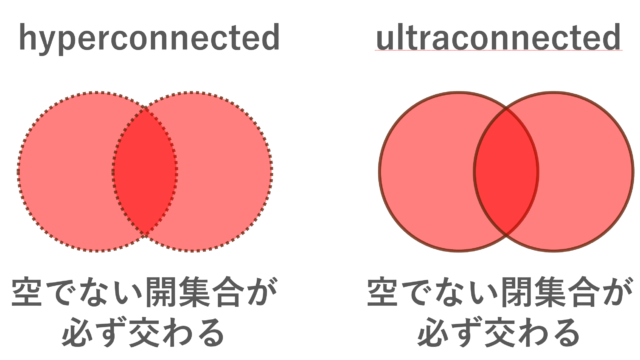 集合と位相
集合と位相