 集合と位相
集合と位相 商位相と商写像
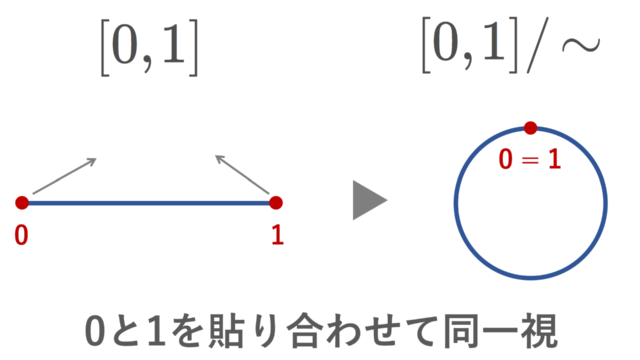
商位相空間とは,位相空間の商集合に定まる位相で,自然な射影を連続写像にする最大・最強の位相です。この時の射影を商写像と言います。幾何学を展開するうえで,商位相の考え方は非常に重要です。商位相と商写像について,定義・具体例・代表的な性質を紹介しましょう。
 集合と位相
集合と位相 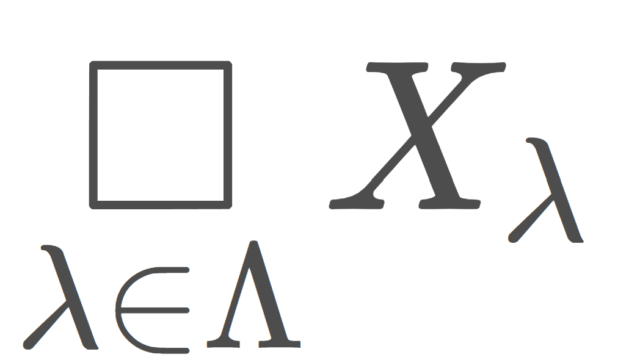 集合と位相
集合と位相 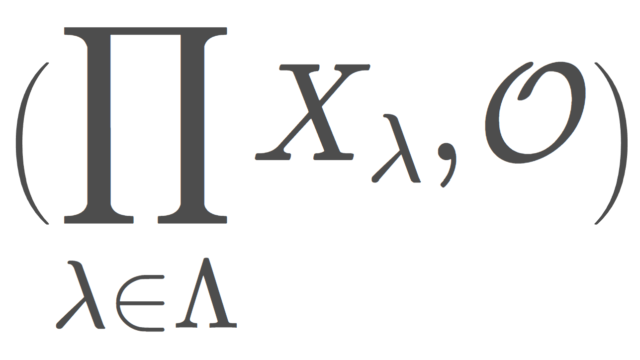 集合と位相
集合と位相  集合と位相
集合と位相 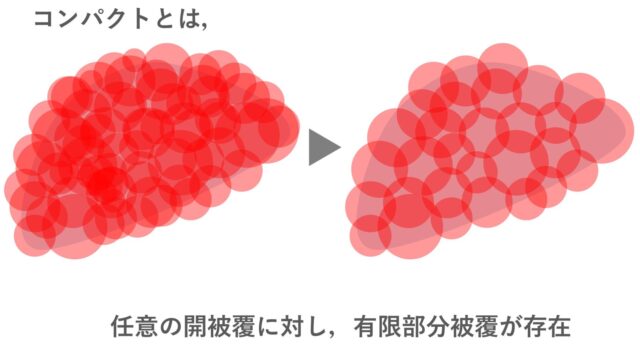 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相