 集合と位相
集合と位相 【位相空間】Irrational Slope Topology
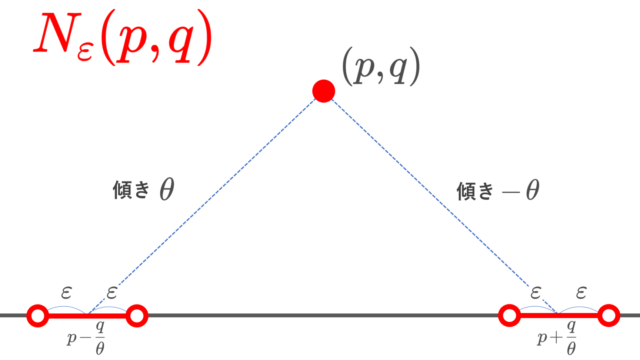
Irrational slope topology とは,xy平面における,上半平面の有理点上で定義される位相で,可算集合でハウスドルフ空間,連結だが弧状連結ではないという性質をもちます。また,ハウスドルフ(T2)なのに,完全ハウスドルフ(T2 1/2)でない例としても挙げられます。
 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 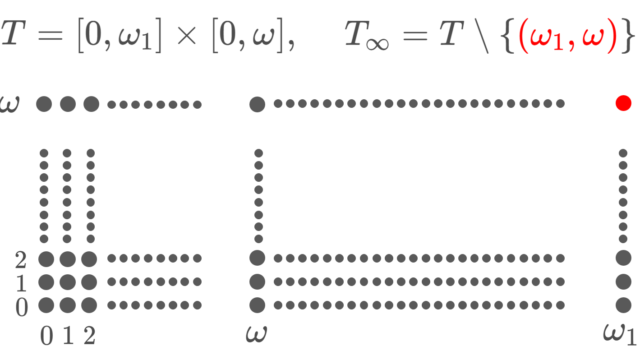 集合と位相
集合と位相 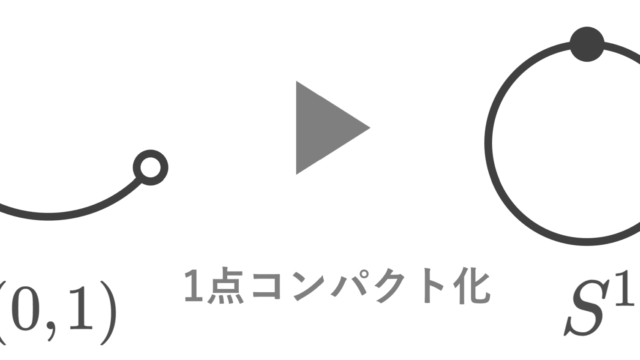 集合と位相
集合と位相 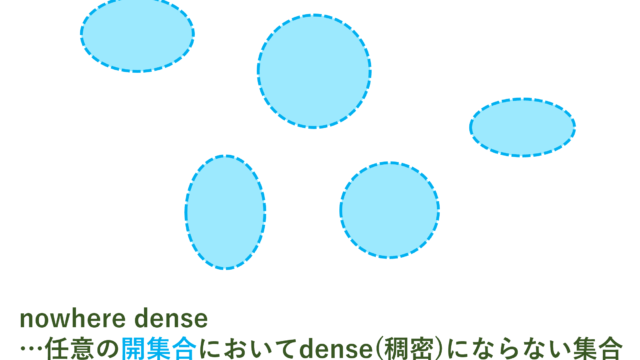 集合と位相
集合と位相  集合と位相
集合と位相 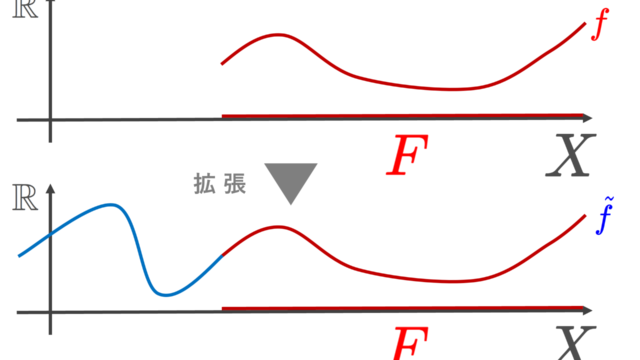 集合と位相
集合と位相 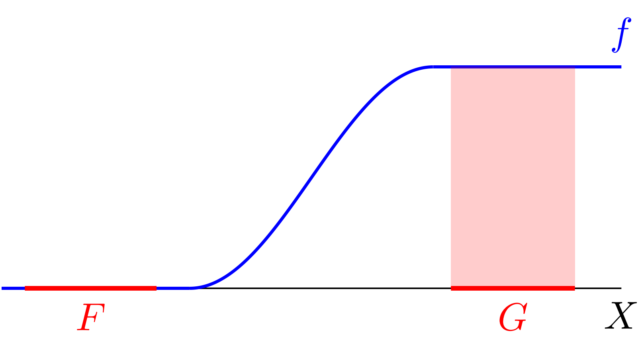 集合と位相
集合と位相 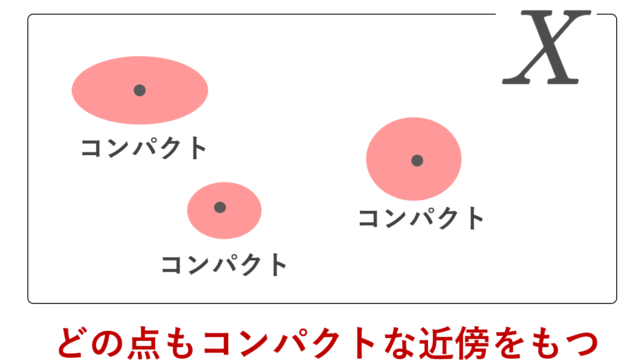 集合と位相
集合と位相