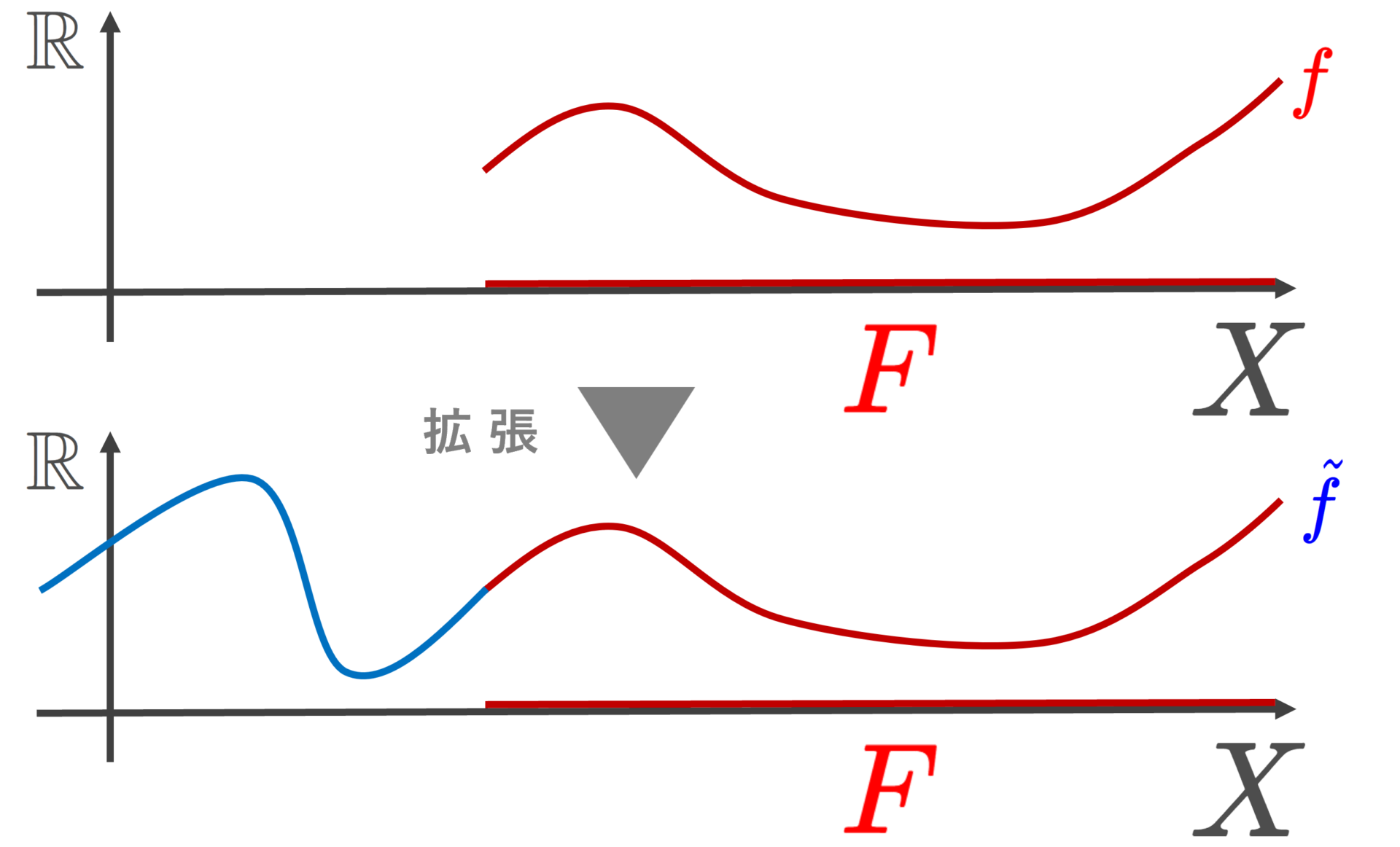
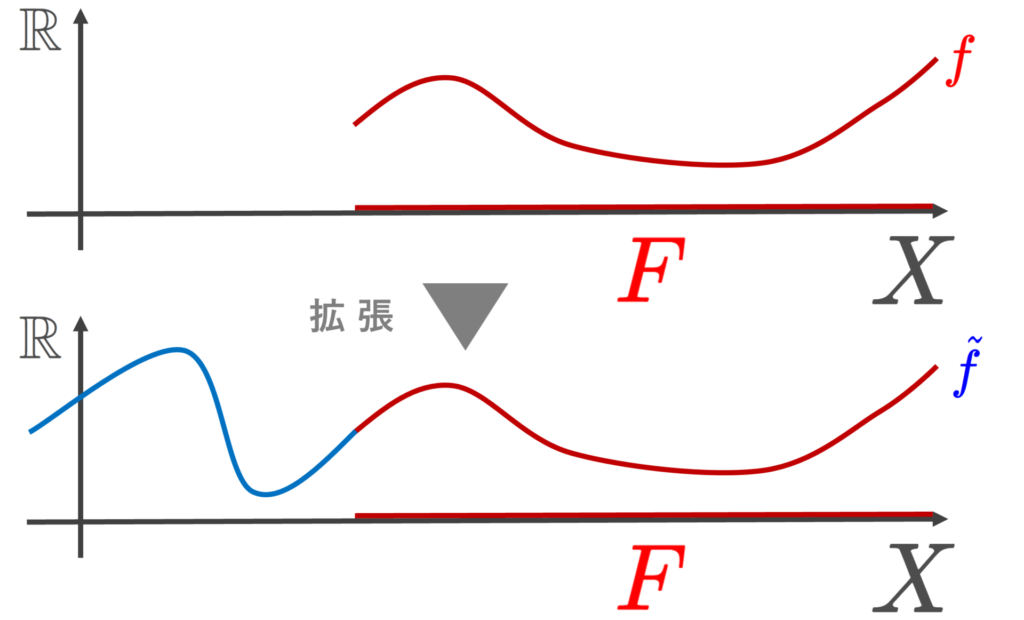
位相空間論におけるティーツェの拡張定理 (Tietze’s extension theorem) とは,正規空間における閉集合上で定義された実連続関数を正規空間全体に連続的に拡張する定理です。
ティーツェの拡張定理とその証明を詳しく紹介しましょう。
ティーツェの拡張定理
本サイトでは,分離公理は一貫して次を採用しています。
| 名称 | 定義 |
|---|---|
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_4 | 任意の2つの互いに素な閉集合 F,G\subset X が開集合で分離される, すなわち F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| 正規 (normal) | T_1 かつ T_4 |
注意ですが,文献によって, T_4 と正規の定義が逆のことがあります。いずれにせよ,今回のティーツェの拡張定理は, T_1 分離公理は仮定しません。主張を見ていきましょう。
ティーツェの拡張定理 (Tietze’s extension theorem)
(X,\mathcal{O}) を位相空間とする。このとき,次の2つは同値である。
\widetilde{f}|_F=f とは, x\in F のとき, \widetilde{f}(x)=f(x) という意味です。
証明には,1.と同値な別の条件を与えるウリゾーンの補題 (Urysohn’s lemma) を使います。
これについては,以下の記事で解説しています。
1.はティーツェの拡張定理内の1.と同じものです。したがって,1. \iff 2. \iff 3.です。証明は,2.\iff 3.を示します。
2.\iff 3.の証明
2. \implies 3.について
F, G\subset X を互いに素な閉集合とする。このとき, F\cup G は閉集合であり, f\colon F\cup G\to \R を
f(F)=\{0\}, \quad f(G)=\{1\}
と定めると,これは連続である。2.の仮定より, f は \widetilde{f}\colon X\to \R に拡張できるが,この \widetilde{f} が3.をみたす。
3. \implies 2.について
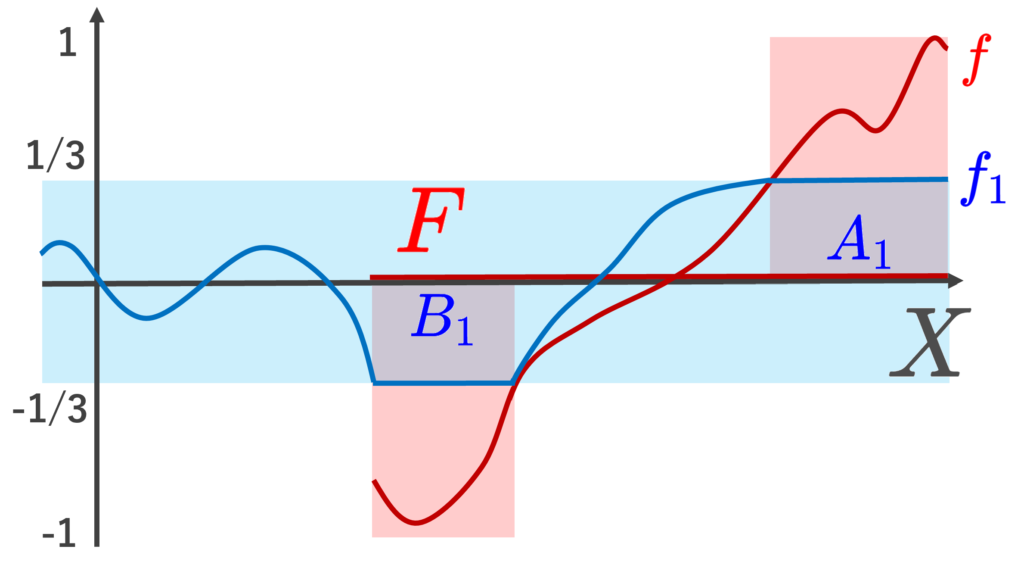
まず, f\colon F\to [-1,1] の場合に示す。
\begin{aligned}A_1&= f^{-1}\left(\left[\tfrac{1}{3}, 1\right]\right), \\ B_1&=f^{-1}\left(\left[-1,-\tfrac{1}{3}\right]\right)\end{aligned}
と定めると, A_1, B_1\subset F は F における互いに素な閉集合であり, F\subset X は X における閉集合なので, A_1, B_1 は X における互いに素な閉集合である。
3.より,連続関数 f_1\colon X\to \left[-\frac{1}{3},\frac{1}{3}\right] で,
f_1(A_1)=\left\{\tfrac{1}{3}\right\},\quad f_1(B_1)=\left\{-\tfrac{1}{3}\right\}
をみたすものが存在する。このとき, \Bigl|f-{f_1}|_F\Bigr|\le \frac{2}{3} である。
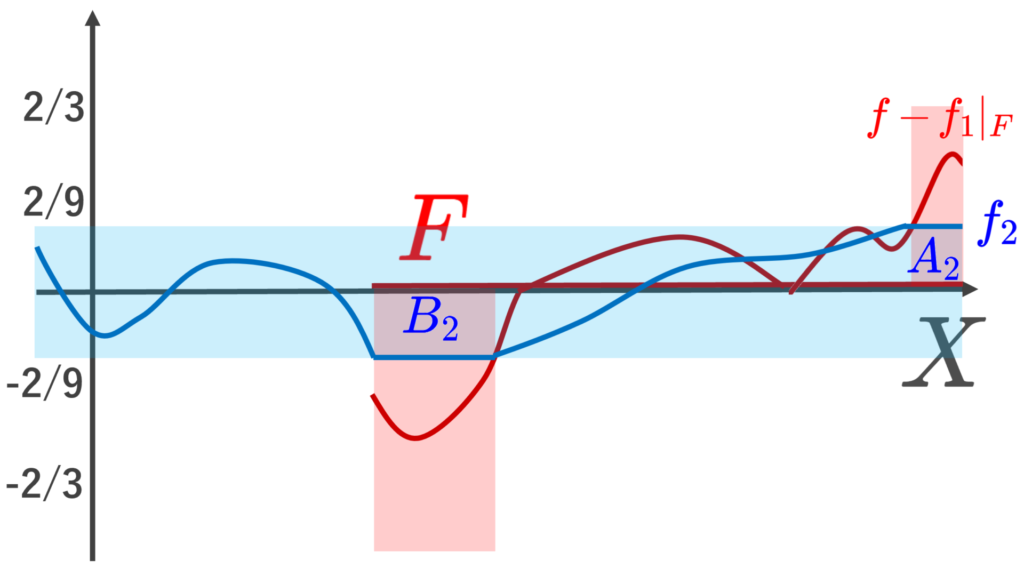
次に, f-f_1|_F \colon F\to \left[-\frac{2}{3},\frac{2}{3}\right] に対し,
\begin{aligned}A_2&= (f-f_1|_F)^{-1}\left(\left[\tfrac{2}{3}\!\cdot\!\tfrac{1}{3}, \tfrac{2}{3}\right]\right), \\ B_2&=(f-f_1|_F)^{-1}\left(\left[-\tfrac{2}{3},-\tfrac{2}{3}\!\cdot\!\tfrac{1}{3}\right]\right)\end{aligned}
と定めると,同様に連続関数 f_2\colon X\to \left[-\tfrac{2}{3}\!\cdot\!\frac{1}{3},\tfrac{2}{3}\!\cdot\!\frac{1}{3}\right] で,
をみたすものが存在する。このとき, \Bigl|f-{f_1}|_F-{f_2}|_F\Bigr|\le \left(\frac{2}{3}\right)^2 である。
同様に帰納的に f_{n-1} まで取れたとして, f-\sum_{k=1}^{n-1}f_k|_F \colon F\to \left[-\left(\frac{2}{3}\right)^{n-1},\left(\frac{2}{3}\right)^{n-1}\right] に対し,
\begin{aligned}A_n&= \left(f-\sum_{k=1}^{n-1}f_k|_F\right)^{-1}\left(\left[\left(\tfrac{2}{3}\right)^{n-1}\tfrac{1}{3}, \left(\tfrac{2}{3}\right)^{n-1}\right]\right), \\ B_n&= \left(f-\sum_{k=1}^{n-1}f_k|_F\right)^{-1}\left(\left[-\left(\tfrac{2}{3}\right)^{n-1},-\left(\tfrac{2}{3}\right)^{n-1}\tfrac{1}{3}\right]\right)\end{aligned}
と定めると,連続関数 f_{n}\colon X\to \left[-\left(\tfrac{2}{3}\right)^{n-1}\tfrac{1}{3}, \left(\tfrac{2}{3}\right)^{n-1}\tfrac{1}{3}\right] で,
をみたすものが存在する。このとき, \Bigl|f-\sum_{k=1}^n{f_k}|_F\Bigr|\le \left(\frac{2}{3}\right)^n である。
\widetilde{f}=\sum_{n=1}^\infty f_n と定めると,
\sum_{n=1}^\infty |f_n| \le \sum_{n=1}^\infty \left(\tfrac{2}{3}\right)^{n-1}\tfrac{1}{3}= 1
であるから,無限和は一様収束である。連続関数の一様収束先は連続であるから, \widetilde{f} は連続,また \widetilde{f}\colon X\to [-1,1] である。さらに \Bigl|f-\sum_{k=1}^n{f_k}|_F\Bigr|\le \left(\frac{2}{3}\right)^n より, \widetilde{f}|_F=f となっており, \widetilde{f} は f の拡張である。
次に,一般の f\colon F\to \R の場合に示す。 (-1,1)\cong \R (同相) であるから, f\colon F\to (-1,1) と思ってよい。さらにこれを f\colon F\to [-1,1] と思うと,上で示したことより, f の拡張 \widetilde{g}\colon X\to [-1,1] が存在する。
ここで,G= \widetilde{g}^{-1}(\{-1,1\}) は F と互いに素な閉集合なので,3.より, h(G)=\{0\}, \, h(F)=\{1\} となる連続関数 h\colon X\to [0,1] が存在する。
\widetilde{f}=h\widetilde{g} と定義すると, \widetilde{f} も f の拡張であり, \widetilde{f}\colon X \to (-1,1)\cong \R となるから,拡張 \widetilde{f} が取れた。
証明終
証明できましたね。