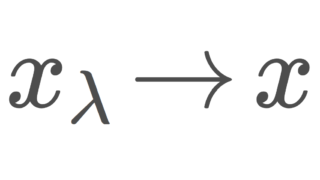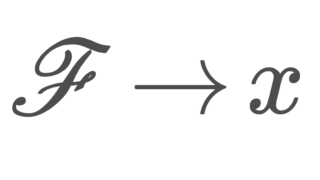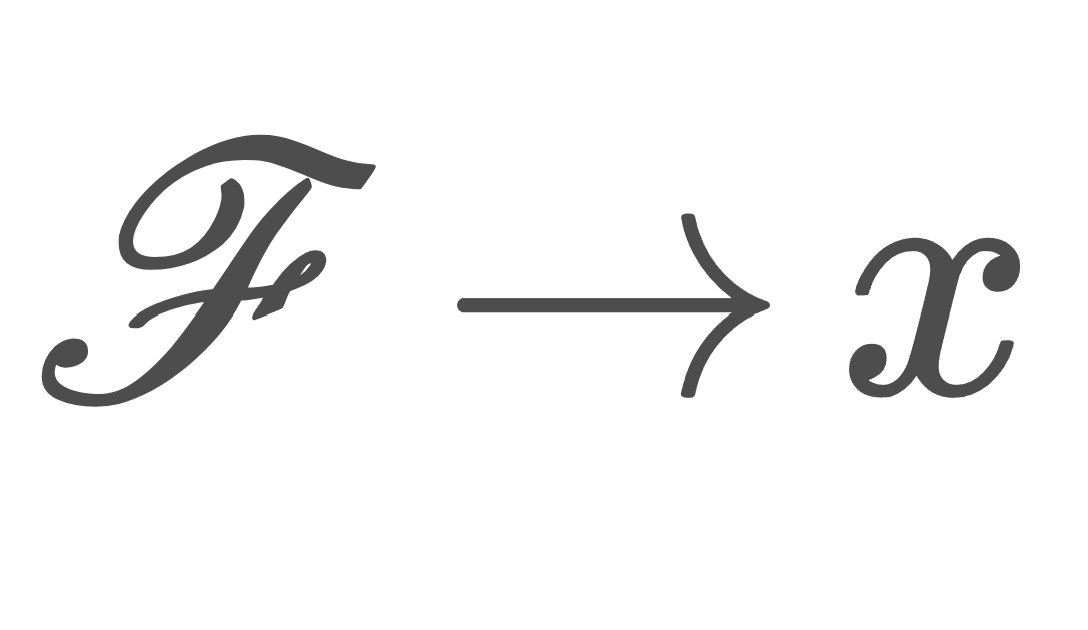普遍ネット(超ネット)の定義と性質

普遍ネット(超ネット)とは，ネットであってかつ，任意の部分集合に対し，その集合またはその補集合に eventually in となるようなものです。点列で考えても面白くない概念で，ネット特有の概念と言えます。

普遍ネットを用いれば，コンパクト性も簡単に記述できます。紹介しましょう。

普遍ネット(超ネット)の定義
普遍ネット(超ネット)にまつわる定理
関連する記事
参考

普遍ネット(超ネット)の定義

本記事では，ネット(有向点族)自体の概念は既知とします。以下で解説しています。

定義（普遍ネット・超ネット）

$X$ を空でない集合とし， $(x_\lambda)\subset X$ をネット(有向点族)とする。

任意の $A\subset X$ に対し， $(x_\lambda)$ is eventually in $A$ または eventually in $X\setminus A$ が成り立つとき， $(x_\lambda)$ を普遍ネット (universal net) または超ネット (ultranet) という。

eventually in $A$ とeventually in $X\setminus A$ が同時に成り立つことはないので，いずれか一方しか成り立ちません。

簡単な例を挙げましょう。

例1(定ネット).

$x_\lambda=x$ となる定ネット $(x_\lambda)$ は普遍ネットである。

$x_\lambda=x$ となる定ネットでは， $x\in A$ のとき，eventually in $A$ であり， $x\notin A$ のときは eventually in $X\setminus A$ です。

点列はネット(有向点族)の一種でした。点列が普遍ネットである条件を考えましょう。

例2(点列が普遍ネットである必要十分条件).

点列 $(x_n)$ が普遍ネットである必要十分条件は，eventually constant であること，すなわちある $N\ge 1$ が存在して， $x_N=x_{N+1}=x_{N+2}=\cdots$ となることである。

eveutually constant であれば，普遍ネットであることは良いでしょう。もし eventually constant でないとしましょう。簡単のため，任意の $m\le n$ で $x_m\ne x_n$ としましょう。このとき，

A = \{ x_{2n} \mid n\ge 1\}

について， $(x_n)$ は not eventually in $A$ かつ not eventually in $X\setminus A$ なので， $(x_n)$ は普遍ネットではありませんね。

普遍ネット(超ネット)にまつわる定理

普遍部分ネットの存在
普遍ネットの基本的性質
コンパクト性と普遍ネット

の順に紹介します。

1. 普遍部分ネットの存在

定理1（普遍部分ネットの存在）

任意のネットは普遍部分ネットが存在する。すなわち，部分ネットで，普遍なものが存在する。

上の例2.と定理1.から分かるように，普遍ネットという概念は，点列にはないネットならではの概念です。しかし，文献[2]いわく，eventually constant でない普遍ネットで，具体的に構成されたものはまだ存在しないとのことです。証明には選択公理を使うので，選択公理を使うことで存在は言えますが，構成はできていないということです。

証明にはフィルターを使いましょう。フィルターと超フィルターについて多少理解していれば大丈夫です。以下で確認してください。

定理1の証明

$X$ を空でない集合とし， $(x_\lambda)\subset X$ をその上のネット(有向点族)とする。

$\mathfrak{F}$ を， $X$ 上のフィルター $\mathscr{F}$ であって，かつ任意の $F\in\mathscr{F}$ に対し， $(x_\lambda)$ is frequently in $F$ となるもの全体の集合とする。 $\{X\}$ はこれをみたすフィルターなので， $\mathfrak{F}$ は空ではない。

$\mathfrak{F}$ は包含順序により，帰納的半順序集合であることが容易に示せる。ツォルンの補題より， $\mathfrak{F}$ には少なくとも一つの極大元 $\mathscr{F}'$ が存在する。この $\mathscr{F}'$ が，超フィルターであること，すなわち任意の $A\subset X$ に対し， $A\in\mathscr{F}'$ または $X\setminus A\in\mathscr{F}'$ をみたすことを示そう。

(i) $(x_\lambda)$ is frequently in $A$ であるが，not frequently in $X\setminus A$ のときを考える。

このとき，任意の $F\in \mathscr{F}'$ に対し， $(x_\lambda)$ is frequently in $F\cap A$ となるから，

\widehat{\mathscr{F}}=\{ G\mid G\supset F\cap A, \, F\in\mathscr{F}'\}

と定めることで， $\mathscr{F}'\subset \widehat{\mathscr{F}}\in\mathfrak{F}$ とできるので， $\mathscr{F}'$ の極大性から， $\mathscr{F}'=\widehat{\mathscr{F}}$ ゆえに $A\in \mathscr{F}'$ である。

(ii) $(x_\lambda)$ is not frequently in $A$ であるが，frequently in $X\setminus A$ のときを考える。(i)と同様で， $X\setminus A\in \mathscr{F}'$ である。

(iii) $(x_\lambda)$ is frequently in $A$ かつ frequently in $X\setminus A$ のときを考える。

もし， $\mathscr{F}'$ が超フィルターでないと仮定すると， $\mathscr{F}'\subsetneq \mathscr{F}''$ となる超フィルター $\mathscr{F}''$ が存在する。このとき， $A\in\mathscr{F}''$ または $X\setminus A\in\mathscr{F}''$ のいずれかが成り立つ。同じことなので， $A\in\mathscr{F}''$ としよう。このとき， $F\in\mathscr{F}'\subset \mathscr{F}''$ に対し， $F\cap A\ne\emptyset$ ，さらに $(x_\lambda)$ is frequently in $F\cap A$ であるから，

\widehat{\mathscr{F}}=\{ G\mid G\supset F\cap A, \, F\in\mathscr{F}'\}

以上から，上の赤字が示せた。最後に，ネット(有向点族)による位相空間論と点列との比較内の定理1の系により，ある部分ネット $(x_{\lambda_\mu})$ が存在して，eventually in $\forall F\in\mathscr{F}$ とできるので，題意は示された。

証明終

2. 普遍ネットの基本的性質

ここでは，普遍ネットの基本的性質を一気に紹介しましょう

定理2（普遍ネットの基本的性質）

普遍ネットの部分ネットは普遍ネットである
普遍ネットが集積点をもてばその点に収束する
$X, Y$ を空でない集合とし， $f\colon X\to Y$ を写像とする(連続でなくてよい)。 $(x_\lambda)\subset X$ を普遍ネットとするとき， $\bigl(f(x_\lambda)\bigr)\subset Y$ も普遍ネットである

1.については，元のネットが eventually in $A$ ならば，部分ネットも eventually in $A$ のはずなので明らかです。

2.については，普遍ネットが frequently in $A$ ならば，eventually in $A$ になるので，言えます。

3.について考えましょう。 $B\subset Y$ について， $(x_\lambda)$ は $X$ 上の普遍ネットより， eventually in $f^{-1}(B)$ か eventually in $X\setminus f^{-1}(B)$ のいずれかが成立します。前者の場合は $\bigl(f(x_\lambda)\bigr)$ is eventually in $B$ であり，後者の場合は $\bigl(f(x_\lambda)\bigr)$ is eventually in $Y\setminus B$ なので，題意は示せました。