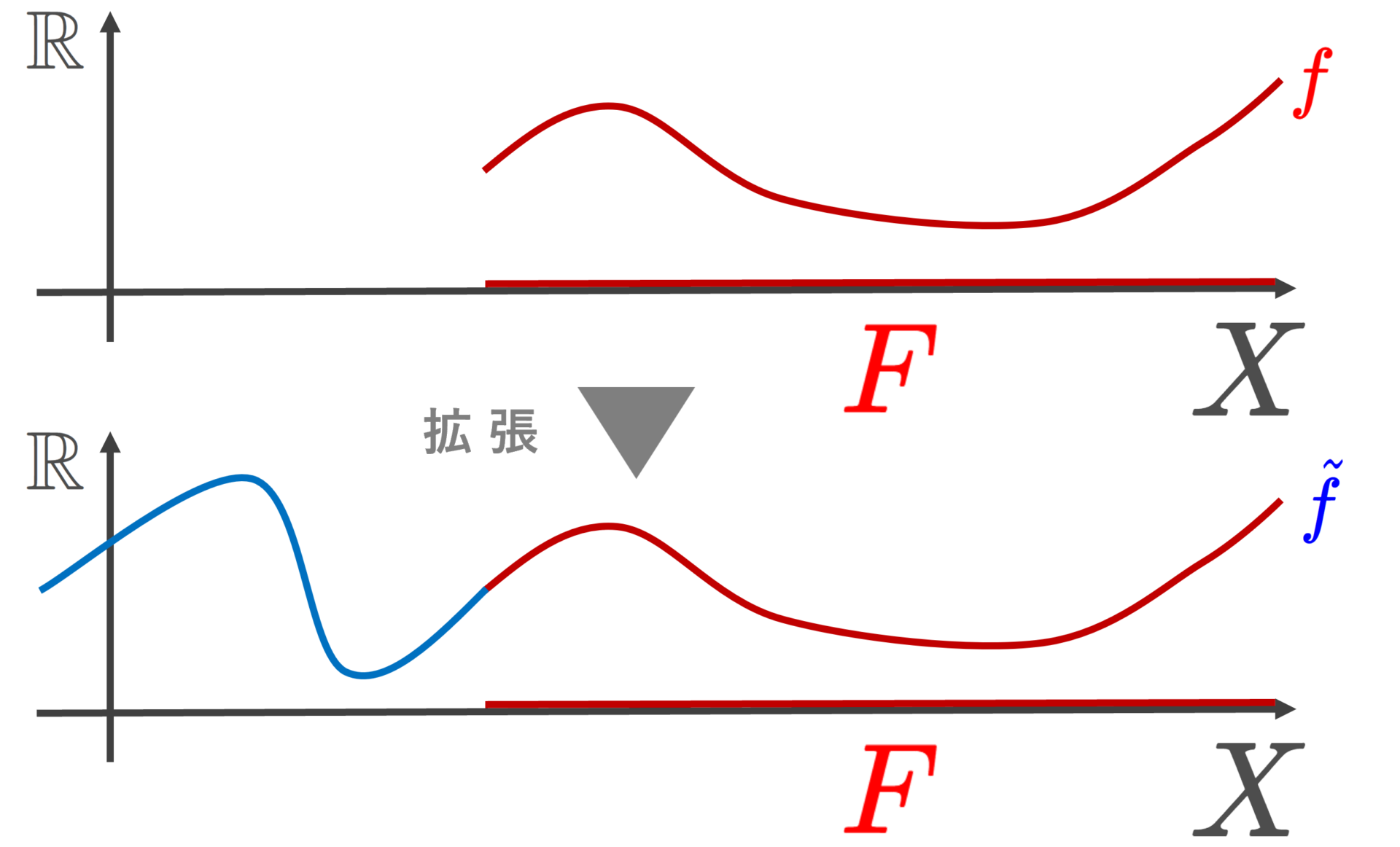
ウリゾーンの補題とは, T_4 空間(正則空間)が連続関数によって分離できるという定理で,ティーツェの拡張定理やウリゾーンの距離化定理の証明など,さまざまな定理の証明に用いられます。ウリゾーンの補題について,その主張と証明をわかりやすく解説します。
ウリゾーンの補題
本サイトでは,分離公理は一貫して次を採用しています。
| 名称 | 定義 |
|---|---|
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_4 | 任意の2つの互いに素な閉集合 F,G\subset X が開集合で分離される, すなわち F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| 正規 (normal) | T_1 かつ T_4 |
注意ですが,文献によって, T_4 と正規の定義が逆のことがあります。いずれにせよ,今回のウリゾーンの補題は, T_1 分離公理は仮定しません。主張を見ていきましょう。
ウリゾーンの補題 (Urysohn’s lemma)
(X,\mathcal{O}) を位相空間とする。このとき,以下は同値である。
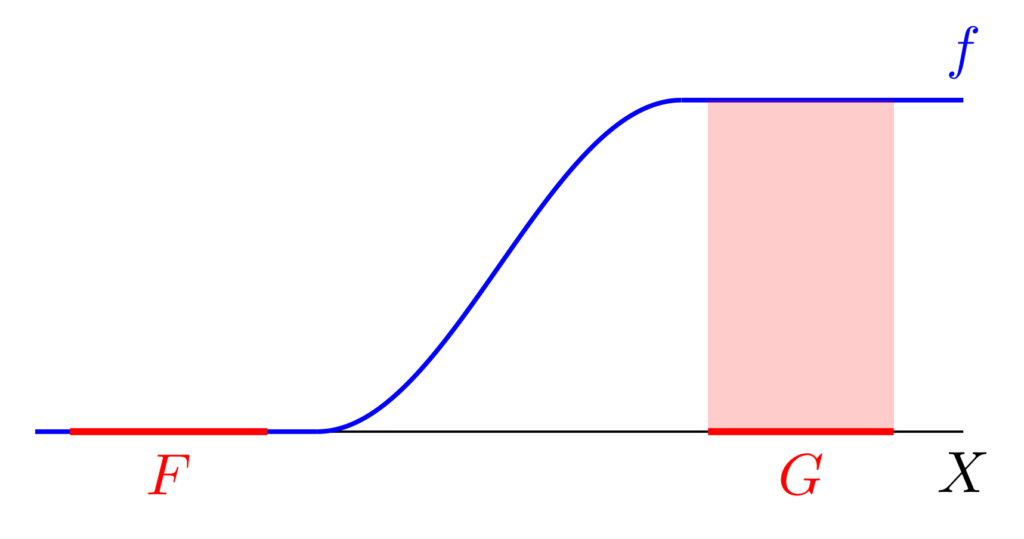
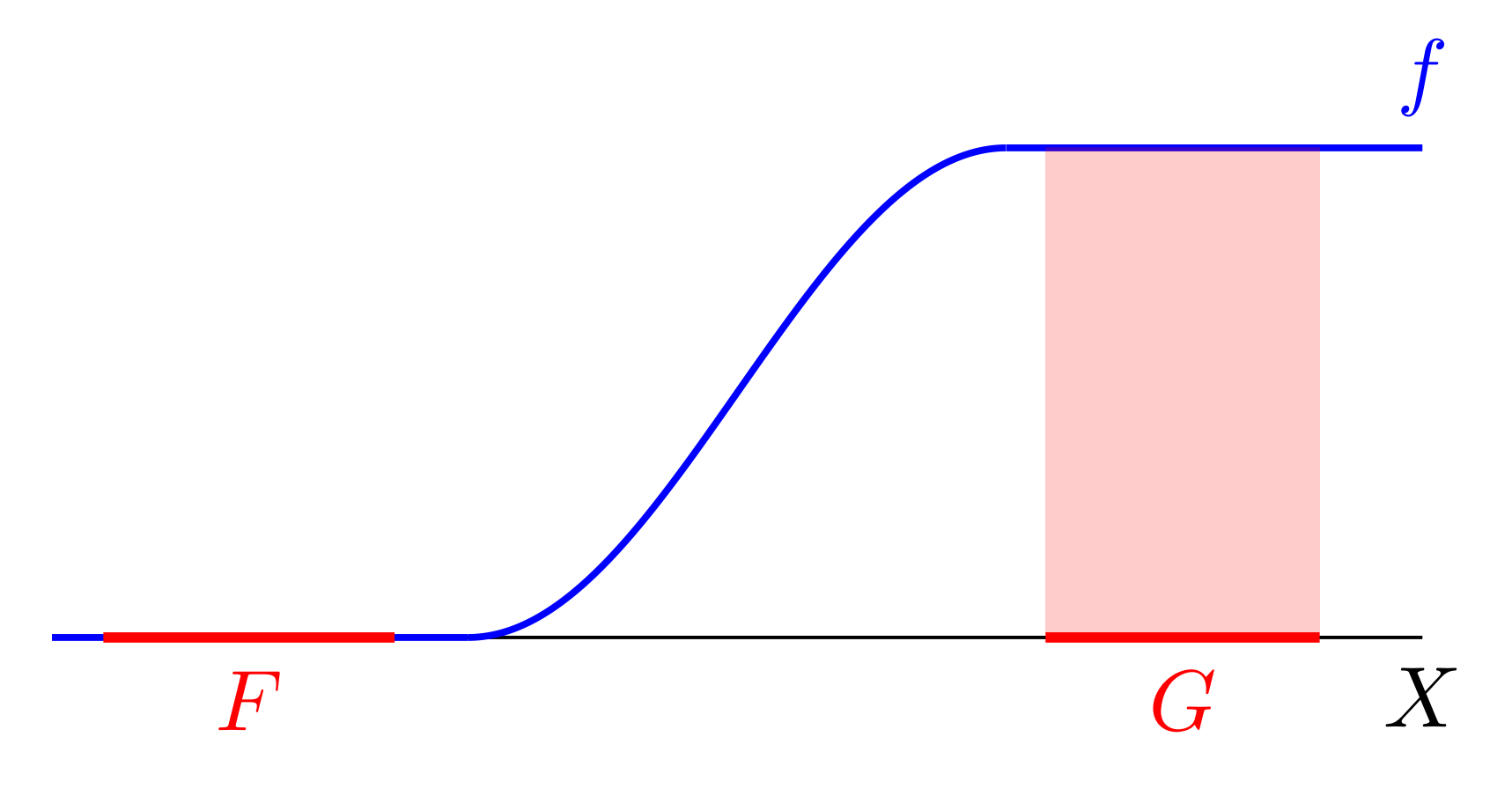
2.のことを,閉集合が連続関数によって分離される (separated) ということがあります。また,2.のような f をウリゾーン関数 (Urysohn function) ということがあります。
2.から T_1 性を導くことはできません。たとえば, X=\{1,2,3,4\},\,\mathcal{O}=\bigl\{\emptyset, \{1,2\}, \{3,4\}, X\bigr\} とし, f(x)=\begin{cases} 0 & x=1,2 \\ 1 & x=3,4\end{cases} とすれば,これは2.をみたし, X は T_4 空間( T_1 とは限らない正規空間)ですが, T_1 空間ではありません。
証明の前に,証明で使う T_4 空間の大事な性質を紹介します。
位相空間 X が T_4 であることと,次は同値:
任意の2つの互いに素な閉集合 F,G\subset X に対し,ある開集合 U で,
F\subset U\subset \overline{U}\subset X\setminus G
となるものが存在する
これは,互いに素な閉集合 F, G が,互いに素な開集合 U, X\setminus \overline{U} で分離できると考えれば,ほぼ明らかでしょう。
これも踏まえて証明します。
証明
2.\implies 1.について
[0,1/2), (1/2, 1] は [0,1] における開集合であり, f は連続であるから,
O_F = f^{-1}([0, 1/2)),\quad O_G=f^{-1}((1/2, 1])
とすれば, O_F, O_G は開集合で, F\subset O_F, \,G\subset O_G,\, O_F\cap O_G=\emptyset であるから, X は T_4 である。
1.\implies 2.について
X は T_4 空間であり,かつ F,G は互いに素な閉集合であるから,
F\subset U_{1/2}\subset \overline{U_{1/2}}\subset X\setminus G
となる開集合 U_{1/2} が存在する。

さらに, F, X\setminus U_{1/2} は互いに素な閉集合であるから,
F\subset U_{1/4}\subset\overline{U_{1/4}}\subset U_{1/2}
となる開集合 U_{1/4} が存在する。同様に, \overline{U_{1/2}}, G は互いに素な閉集合であるから,
となる開集合 U_{3/4} が存在する。
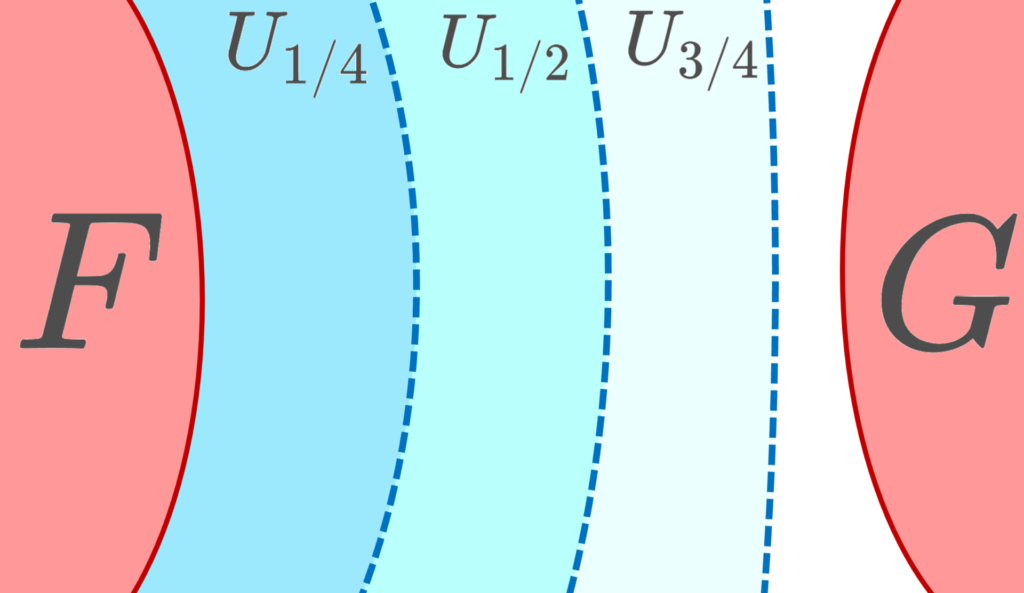
同様のことを帰納的に繰り返して, D= \{ k/2^n\mid n\ge 1, k=1,2,\ldots, 2^n-1\} の各元 d\in D に対し,開集合 U_d を取る。ここで, f\colon X\to [0,1] を
f(x) = \begin{cases} \inf_{x\in U_d} d & x\in \bigcup_{d\in D} U_d ,\\ 1 & \text{otherwise} \end{cases}
と定めると, x\in F のとき, x\in U_d \;(\forall d\in D) であり, x\in G のとき x\notin \bigcup_{d\in D} U_d なので,
となる。最後, f が連続であることを示そう。 \varepsilon>0 とし, x\in X とする。
f(x)=0 のとき,ある d\in D\cap (0,\varepsilon) を取ると, x\in U_d であり, U_d は開集合なので, x に十分近い y で f(y)<\varepsilon すなわち |f(y)-f(x)|<\varepsilon となる。
f(x)=1 のとき,ある d\in D\cap (1-\varepsilon , 1) を取ると, x\in X\setminus \overline{U_d} であり, X\setminus \overline{U_d} は開集合なので, x に十分近い y で f(y)>1-\varepsilon すなわち |f(y)-f(x)|<\varepsilon となる。
0<f(x)<1 のとき,ある d_1\in D\cap \bigl(f(x)-\varepsilon, f(x)\bigr),\, d_2\in D\cap \bigl(f(x), f(x)+\varepsilon\bigr) を取ると, x\in U_{d_2}\setminus \overline{U_{d_1}} であり,U_{d_2}\setminus \overline{U_{d_1}} は開集合なので, x に十分近い y で |f(y)-f(x)|<\varepsilon となる。
ゆえに, f が連続であることが示せたので,証明が終わる。
証明終
\{U_d\} を構成して,その \inf d で f(x) を定義するだけで,連続関数が作れるのは面白いですね。
ウリゾーンの補題は,選択公理が必要だと言われることがありますが,実際にそうです。 \{U_d\} を帰納的にとるところで,選択公理を使っています。
なお, (X, d) が距離空間の場合は,互いに素な閉集合 F, G に対し,単に
f(x)=\frac{d(x, F)}{d(x,F)+d(x,G)}
とすればよいです。ただし, d(x,F)=\inf_{a\in F}d(x,a) であり, d(x,G) も同様です。
T2空間・T3空間では同じことは成立しない
ウリゾーンの補題は T_4 空間における定理であり, T_2, T_3 空間では同じことは成立しません。定理として述べておきましょう。まずは分離公理を復習します。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_2 ハウスドルフ | 任意の異なる2点 x,y\in X が開集合で分離される, すなわち x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_{2 \frac {1}{2}} 完全ハウスドルフ | 任意の異なる2点 x,y\in X が閉近傍で分離される, すなわち x\in O_x, \, y\in O_y,\, \overline{O_x}\cap \overline{O_y}=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F が開集合で分離される, すなわち F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| 正則 (regular) | T_0 かつ T_3( \iff T_2 かつ T_3) ※ 正則と T_3 の定義を逆にすることがある |
定理1( T_2 空間におけるウリゾーン関数)
(X,\mathcal{O}) を位相空間とする。このとき,
- X は T_2 空間(ハウスドルフ空間)である
- X は T_{2 \frac {1}{2}} 空間(完全ハウスドルフ空間)である
- 任意の異なる2点 x,y\in X に対し,連続関数 f\colon X\to [0,1] で,
f(x)=0, \quad f(y)=1
となるものが存在する(ウリゾーン空間 (Urysohn space) という)
について,3.\implies 2.\implies 1.は成立するが,逆は成立しない。
3.\implies 2.は, f^{-1}([0,1/3]), f^{-1}([2/3,1]) とすれば,これはそれぞれ x, y の閉近傍になっています。逆が成立しないことは今は紹介しません。なお,文献によっては,完全ハウスドルフ空間とウリゾーン空間の定義を逆にすることがあります。
定理2( T_3 空間におけるウリゾーン関数)
(X,\mathcal{O}) を位相空間とする。このとき,
- X は T_3 空間( T_0 とは限らない正則空間)である
- 任意の閉集合 F と任意の x\notin F に対し,連続関数 f\colon X\to [0,1] で,
f(x)=0, \quad f(F)=\{1\}
となるものが存在する( T_{3\frac{1}{2}} 空間という)
について,2.\implies 1.は成立するが,逆は成立しない。
2.\implies 1.は, f^{-1}([0,1/3)), f^{-1}((2/3,1]) とすれば,これはそれぞれ x, F の開近傍になっています。逆が成立しないことは今は紹介しません。