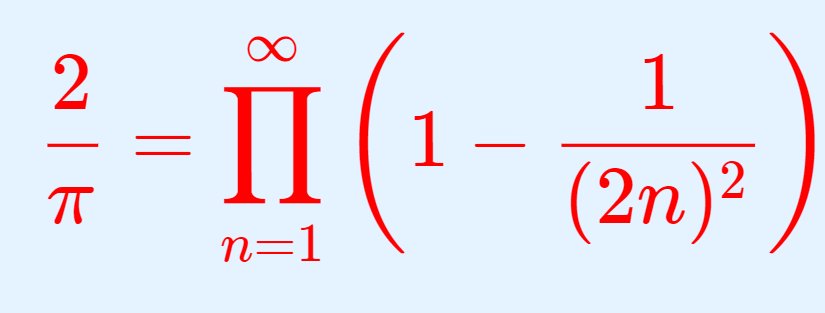ウォリスの公式(ワリスの公式)と呼ばれる公式を3つの形で紹介し,それらの公式を証明します。
ウォリスの公式
定理(ウォリスの公式; Wallis formula)
\small \color{red} \begin{aligned}\sqrt{\pi} &= \lim_{n\to\infty} \frac{1}{\sqrt{n}} \frac{(2n)!!}{(2n-1)!!} =\lim_{n\to\infty} \frac{2^{2n}}{\sqrt{n}}\frac{(n!)^2}{(2n)!}, \\ \frac{\pi}{2} &= \prod_{n=1}^\infty \frac{(2n)^2}{(2n-1)(2n+1)} = \frac{2^2}{1\cdot 3}\cdot \frac{4^2}{3\cdot 5} \cdots ,\\ \frac{2}{\pi}&= \prod_{n=1}^\infty \!\left( 1-\frac{1}{(2n)^2}\right) = \left(1-\frac{1}{2^2}\right) \!\! \left(1-\frac{1}{4^2}\right)\cdots. \end{aligned}
n!! は2重階乗の記号で,定義は
\small n!! =\begin{cases} n(n-2)(n-4) \dots 3 \cdot 1 & \text{if } n \text{ is odd,} \\ n(n-2)(n-4) \dots 4 \cdot 2 & \text{if } n \text{ is even,} \end{cases}
0!! =(-1)!! = 1 です。(ただし, \text{odd, even} はそれぞれ奇数・偶数の英語です。)
円周率 \pi が登場する,きれいな公式の1つですね。実際のところは,収束のスピードは遅く,円周率の近似計算には使えないようです。
ウォリスの公式の証明
ウォリスの公式の証明には,以下のウォリス積分を用います。確認をしていきましょう。
n \ge 0 に対し,
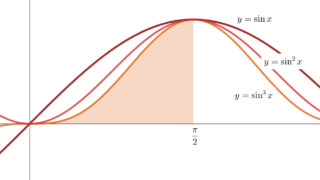
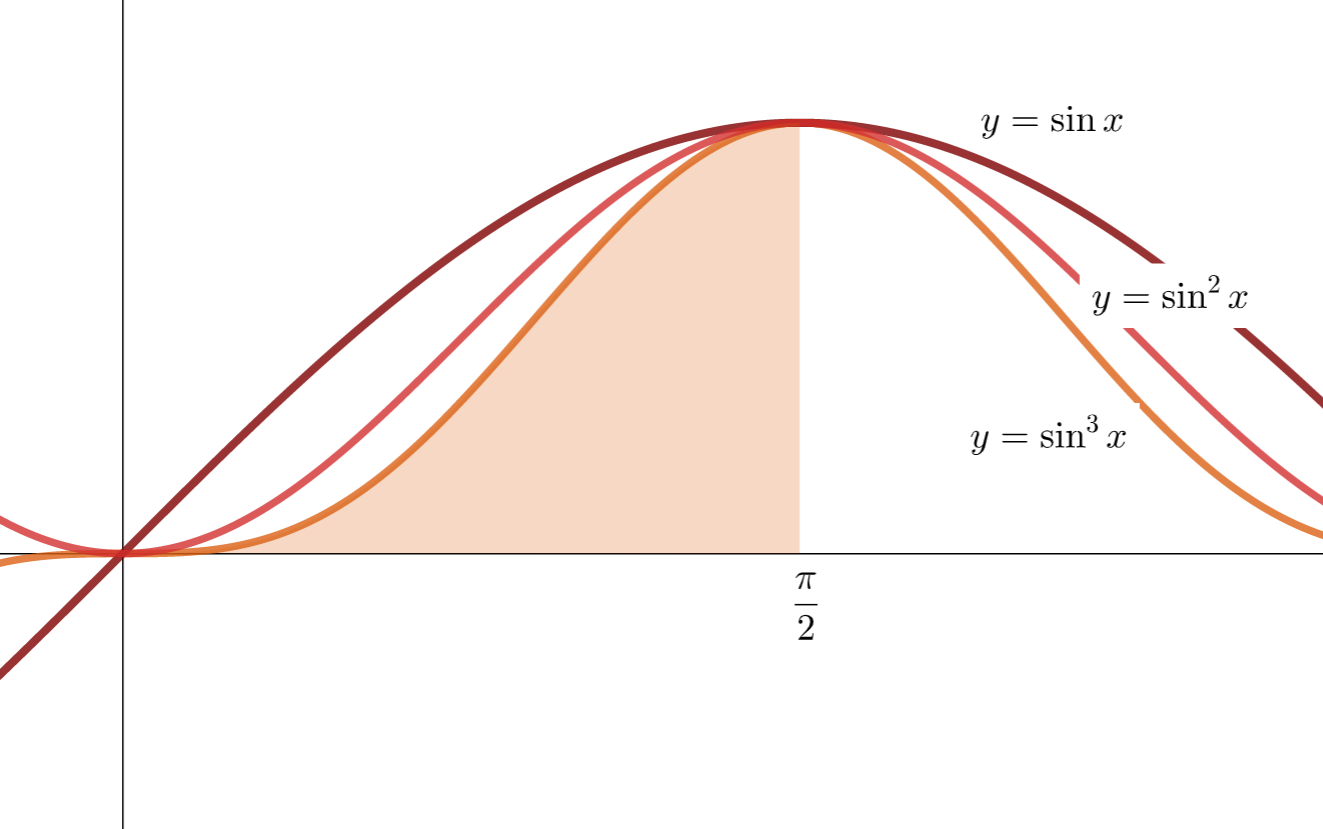
\begin{aligned} &\int_0^{\frac{\pi}{2}} \sin^n x \, dx \\ &=\begin{dcases} \frac{(n-1)!!}{n!!} & \text{if } n \text{ is odd,}\\ \frac{\pi}{2}\frac{(n-1)!!}{n!!} & \text{if }n \text{ is even.}\end{dcases}\\ \end{aligned}これの証明は, I_n= \int_0^{\frac{\pi}{2}} \sin^n x とおき,部分積分の公式を用いて I_n の漸化式を作ることで可能です。詳しくは,以下の記事で解説しています。
では,ウォリスの公式を証明していきましょう。
証明
\displaystyle \sqrt{\pi} = \lim_{n\to\infty} \frac{1}{\sqrt{n}} \frac{(2n)!!}{(2n-1)!!} =\lim_{n\to\infty} \frac{2^{2n}}{\sqrt{n}}\frac{(n!)^2}{(2n)!} について
I_n= \int_0^{\frac{\pi}{2}} \sin^n x とおく。 \sin^{2n+1} x \le \sin^{2n} x \le \sin^{2n-1} x であるから,その積分についても I_{2n+1} \le I_{2n} \le I_{2n-1} である。ウォリス積分を用いると,
\frac{(2n)!!}{(2n+1)!!} \le \frac{\pi}{2}\frac{(2n-1)!!}{(2n)!!} \le \frac{(2n-2)!!}{(2n-1)!!} .
各辺 \dfrac{1}{\pi}\dfrac{(2n-1)!!}{(2n-2)!!} を掛けると,
故に, \displaystyle \lim_{n\to\infty} n \left\{ \frac{(2n-1)!!}{(2n)!!} \right\}^2 = \frac{1}{\pi}. これから,
がわかる。後半の等式は,2重級数に関する等式
から従う。
残りの2式について
\frac{(2n)!!}{(2n+1)!!} \le \frac{\pi}{2}\frac{(2n-1)!!}{(2n)!!} \le \frac{(2n-2)!!}{(2n-1)!!}
までは上と同じ。各辺 \dfrac{2}{\pi}\dfrac{(2n+1)!!}{(2n)!!} を掛けると,
\frac{2}{\pi} \le \frac{(2n-1)!!(2n+1)!!}{\{(2n)!!\}^2} \le \frac{2}{\pi}\frac{2n+1}{2n} .
故に, \displaystyle \lim_{n\to\infty} \frac{(2n-1)!!(2n+1)!!}{\{(2n)!!\}^2}=\frac{2}{\pi}. ここで,
\begin{aligned}\frac{(2n-1)!!(2n+1)!!}{\{(2n)!!\}^2}&= \prod_{k=1}^n \frac{(2k-1)(2k+1)}{(2k)^2}\\ &= \prod_{k=1}^n \left(1-\frac{1}{(2k)^2} \right) \end{aligned} であるから,
\frac{2}{\pi}=\prod_{n=1}^\infty \left(1-\frac{1}{(2n)^2} \right).
逆数を取ると,
もわかる。
証明終
ウォリスの公式からスターリングの公式へ
ウォリスの公式を用いて証明される有名な定理として,スターリングの公式があります。スターリングの公式とは, n! を近似する公式です。主張のみ述べましょう。
定理(スターリングの公式; Stirling’s formula)
\color{red} n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n.
ここで, f(x) \sim g(x) とは, f(x)/g(x) \xrightarrow{x\to\infty} 1 を意味する。
これの証明は,以下の記事で解説しています。