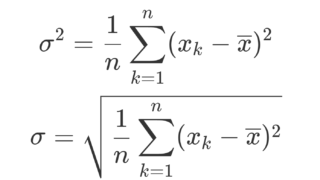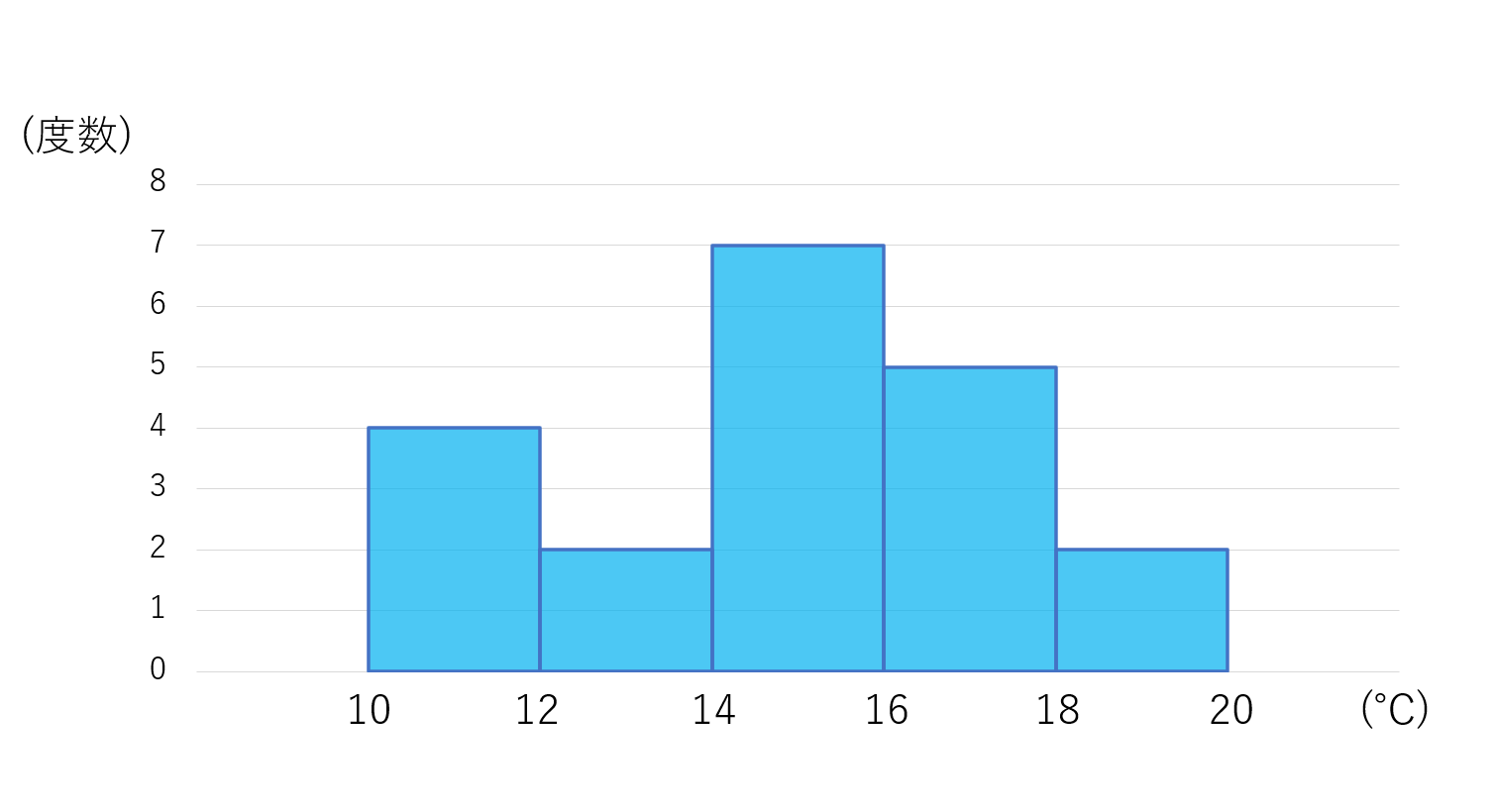数量データにおける平均値・中央値・最頻値の定義と,その意味を具体例を含めて解説し,さらに棒グラフとの関係,ヒストグラムとの関係を紹介します。
データの平均値・中央値・最頻値
定義(データの平均値・中央値・最頻値)
- データ x_1,x_2,\dots, x_n に対し,これらを全て足してデータの大きさ n で割ったもの
\color{red}\overline{x} = \frac{x_1+x_2+\dots +x_n}{n} \left(= \frac{1}{n}\sum_{k=1}^n x_k\right)
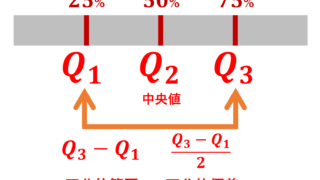
をデータの平均 (平均値; average, mean) という。 - データを昇順に並べたもの x_1\le x_2\le \dots \le x_n に対し,その真ん中の値( n が偶数のときは真ん中の2つの平均)
\color{red}\text{median} = \begin{dcases} x_{k} & n =2k-1,\\[3pt] \frac{x_{k}+x_{k+1}}{2} &n=2k\end{dcases}
を中央値 (median) という。 - データ x_1,x_2,\dots, x_n に対し,一番多く出現する値を最頻値 (mode) という。
最頻値は複数ある可能性があります。また,全ての値が一回ずつ登場する場合は「最頻値なし」と考えることにします。
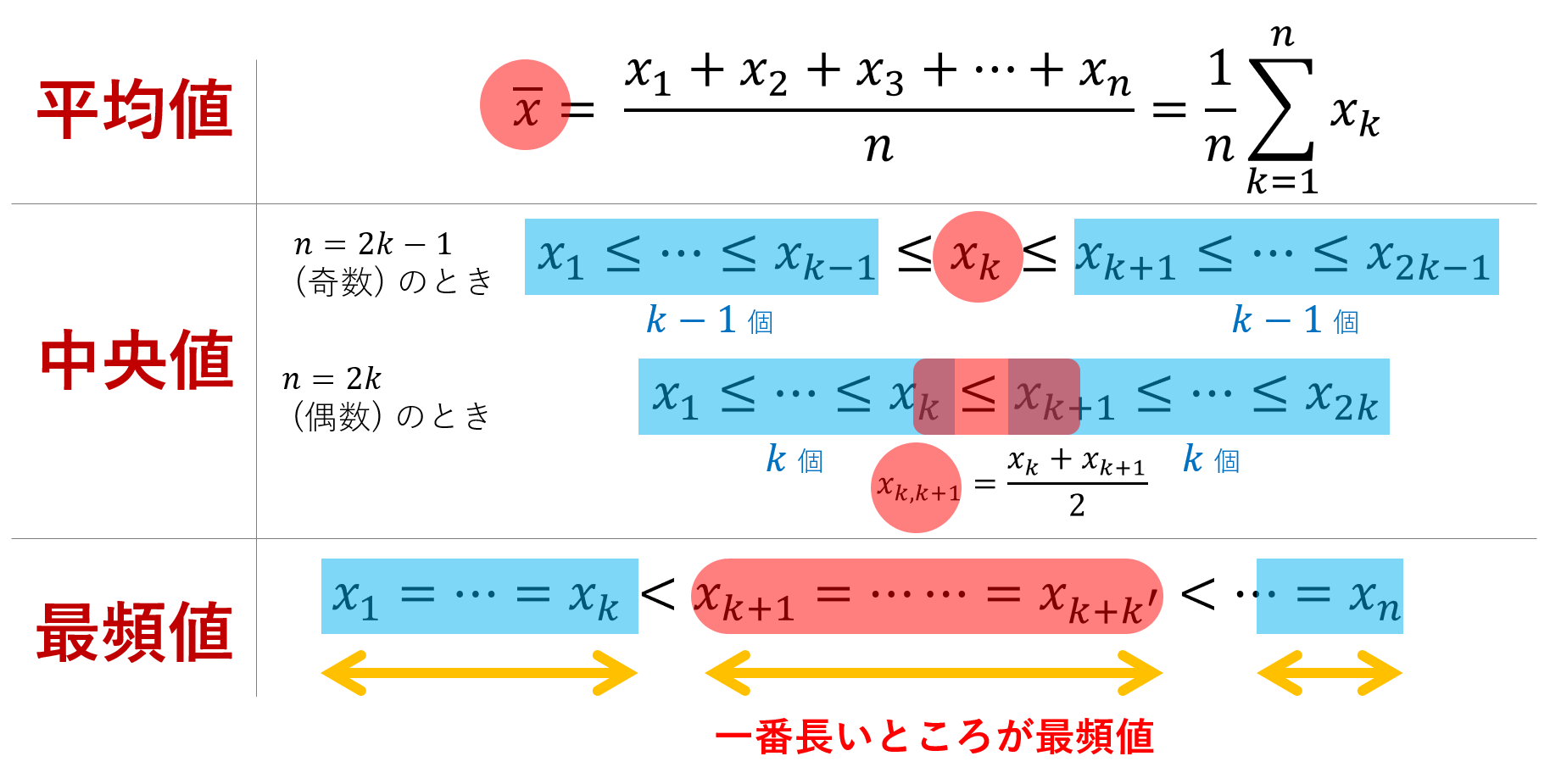
図解すると以下のような感じですね。
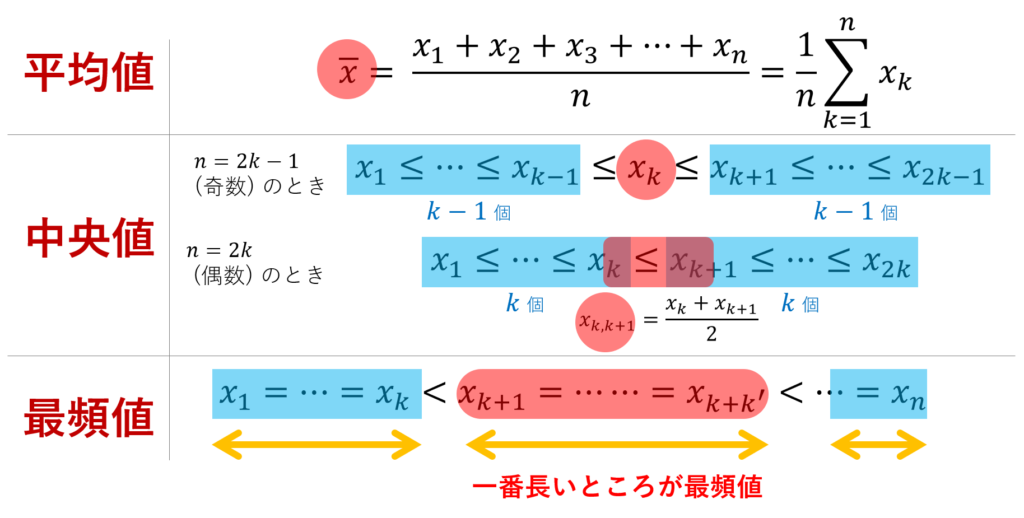
有名ですが大事な注意として,平均値は真ん中の値(中央値)ではないということです。平均値は例えば最大値が増えると増えますが,中央値は最大値が増えても変わりません。
日本の平均年収は440万円ほどですが,中央値は370万円ほどです。これは,年収がとても高い人が平均を吊り上げているからです。
実際に具体例を挙げ,確認していきましょう。
例1.
5人でテストを行ったところ,それぞれの点数は 10, 30, 60, 80,80 点であった。このとき,
平均は \dfrac{10+30+60+80+80}{5} = \dfrac{260}{5}=52 点であり,
中央値は真ん中の値なので 60 点,
最頻値は一番多く登場する値なので 80 点である。
52<60 となっており,平均よりも中央値の方が大きいですが,これは 80 点の人が平均を上げている以上に, 10 点や 30 点の人が平均を下げているからといえるでしょう。
ちなみに, 10 点の人が代わりに 30 点を取ったとすると,平均値は 54 点に上がりますが,中央値や最頻値はそのままです。平均値は全員の値が影響しますが,中央値や最頻値は必ずしもそうではないということが分かりますね。
例2.
6人の年収は 100, 100, 300, 400, 800, 1000 万円であった。このとき,
6人の平均年収は \dfrac{100+100+300+400+800+1000}{6}=450 万円,
年収の中央値は \dfrac{300+400}{2}=350 万円,
年収の最頻値は 100 万円である。
今の日本の縮図のような6人かもしれませんね。やはり,平均値は真ん中の値(中央値)とは異なっており,平均値を超えているのは6人中2人のみです。
グラフと平均値・中央値・最頻値
棒グラフとの関係,ヒストグラムとの関係を述べましょう。
棒グラフと平均値・中央値・最頻値
棒グラフと平均値・中央値・最頻値との関係を考えましょう。以下のような,各人のテストの成績を昇順に並べた棒グラフがあったときに,平均値・中央値・最頻値はどこになるでしょうか。
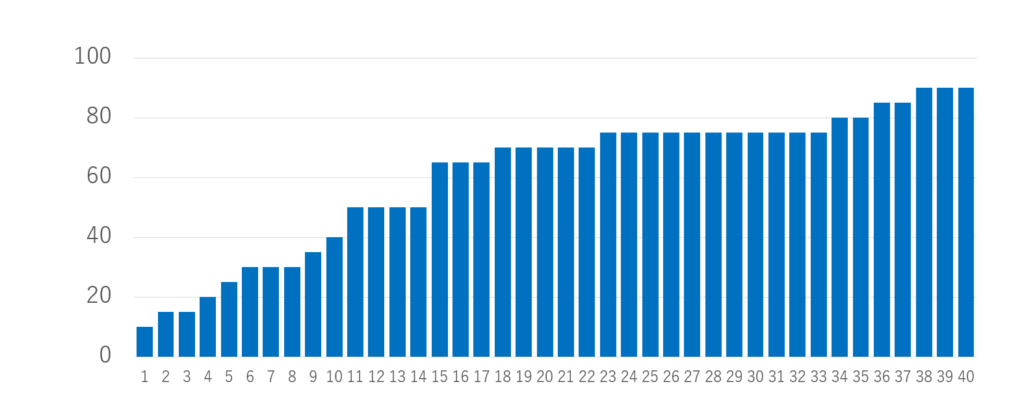
答えは以下のようになります。
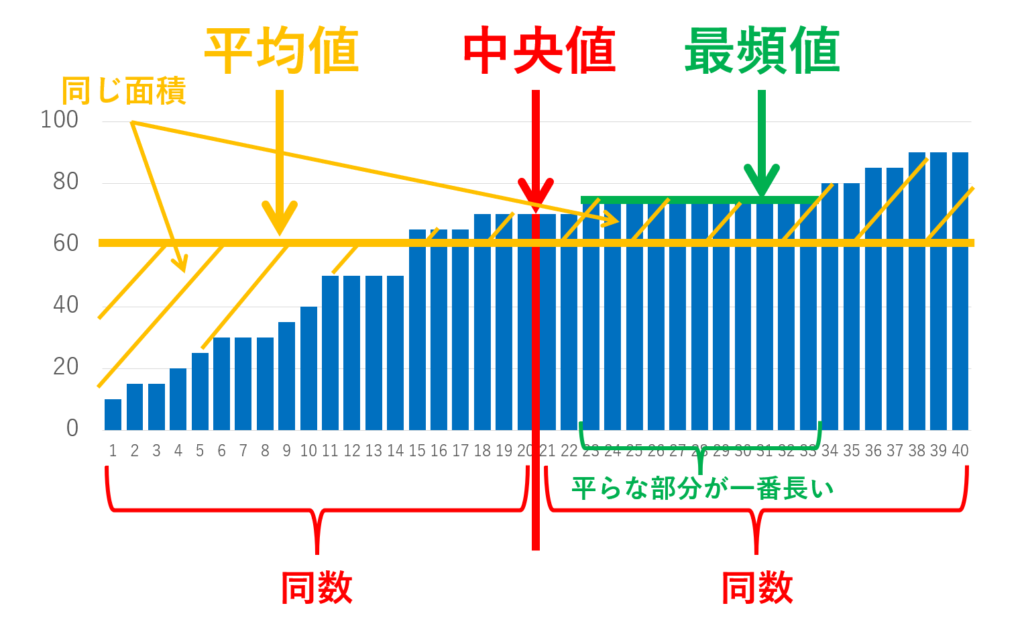
それぞれの定義を考えてみればわかるでしょう。
ヒストグラムと平均値・中央値・最頻値
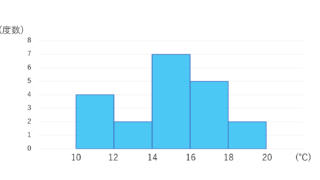
続いてヒストグラムです。ヒストグラムは横軸に階級,縦軸に人数などの度数を取り,本来「ざっくりとした分布をみるためのもの」です。たとえば,テストの成績の場合,横軸が点数で,縦軸がその点を取った人数です。
しかし,今回はヒストグラムは仮想的に「連続」にかくことで,分布を正確に捉えることにしましょう。
さて,以下のヒストグラムにおいて,平均値・中央値・最頻値はどこにあたるでしょうか。
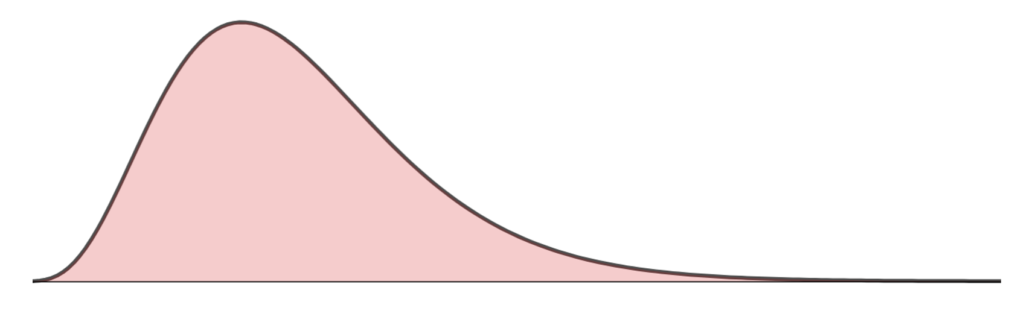
答えは以下のようになります。
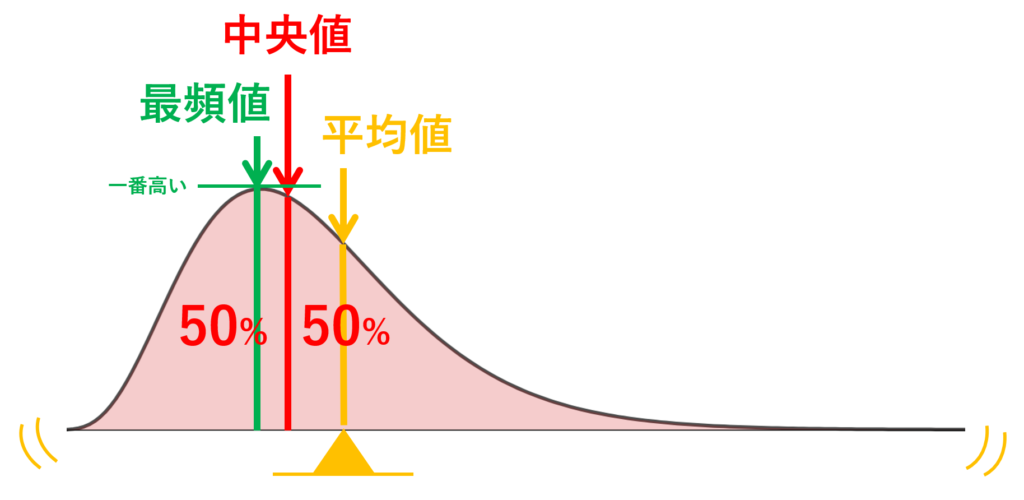
これも,それぞれの値の定義を考えればわかるでしょう。平均値が「てこの原理」の釣り合いのところというのは面白いですね。