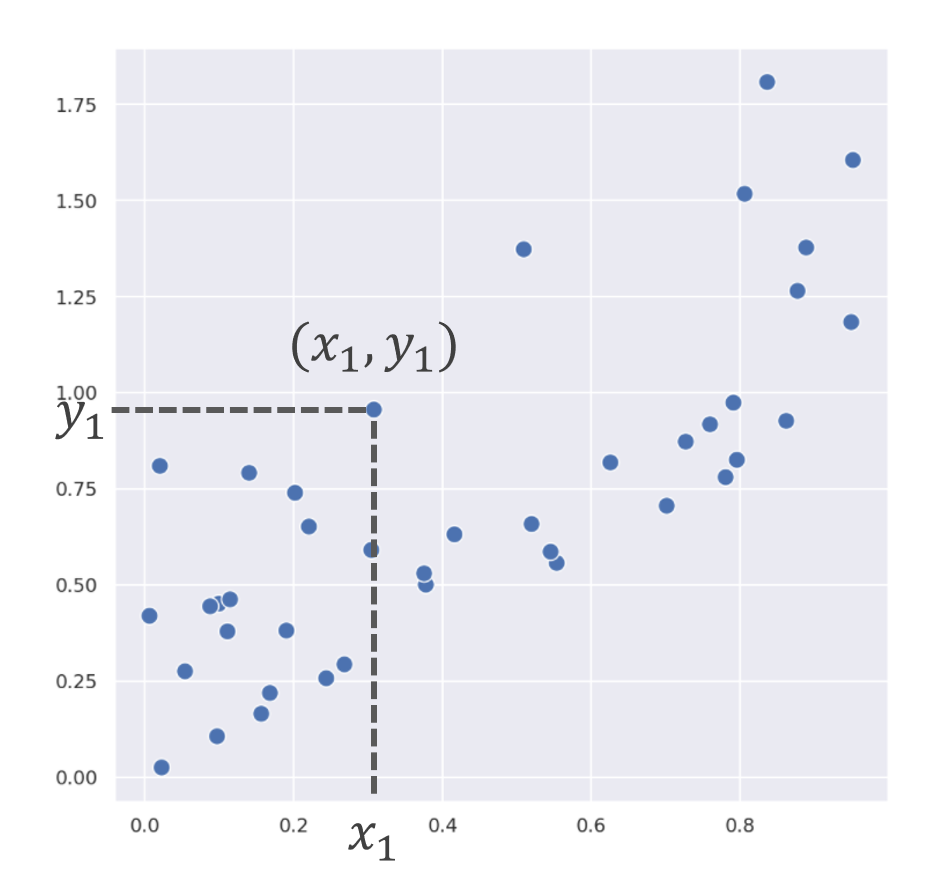
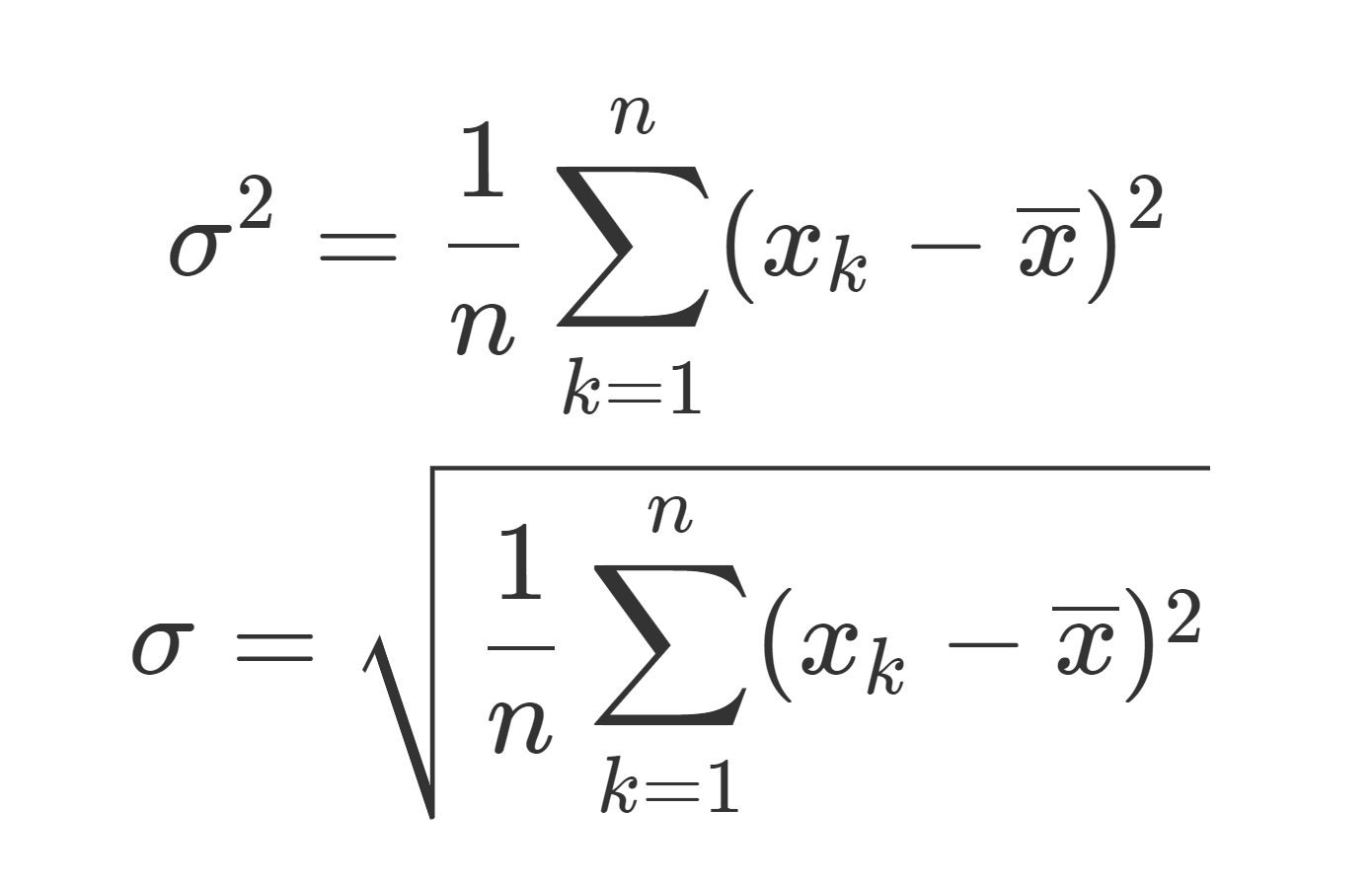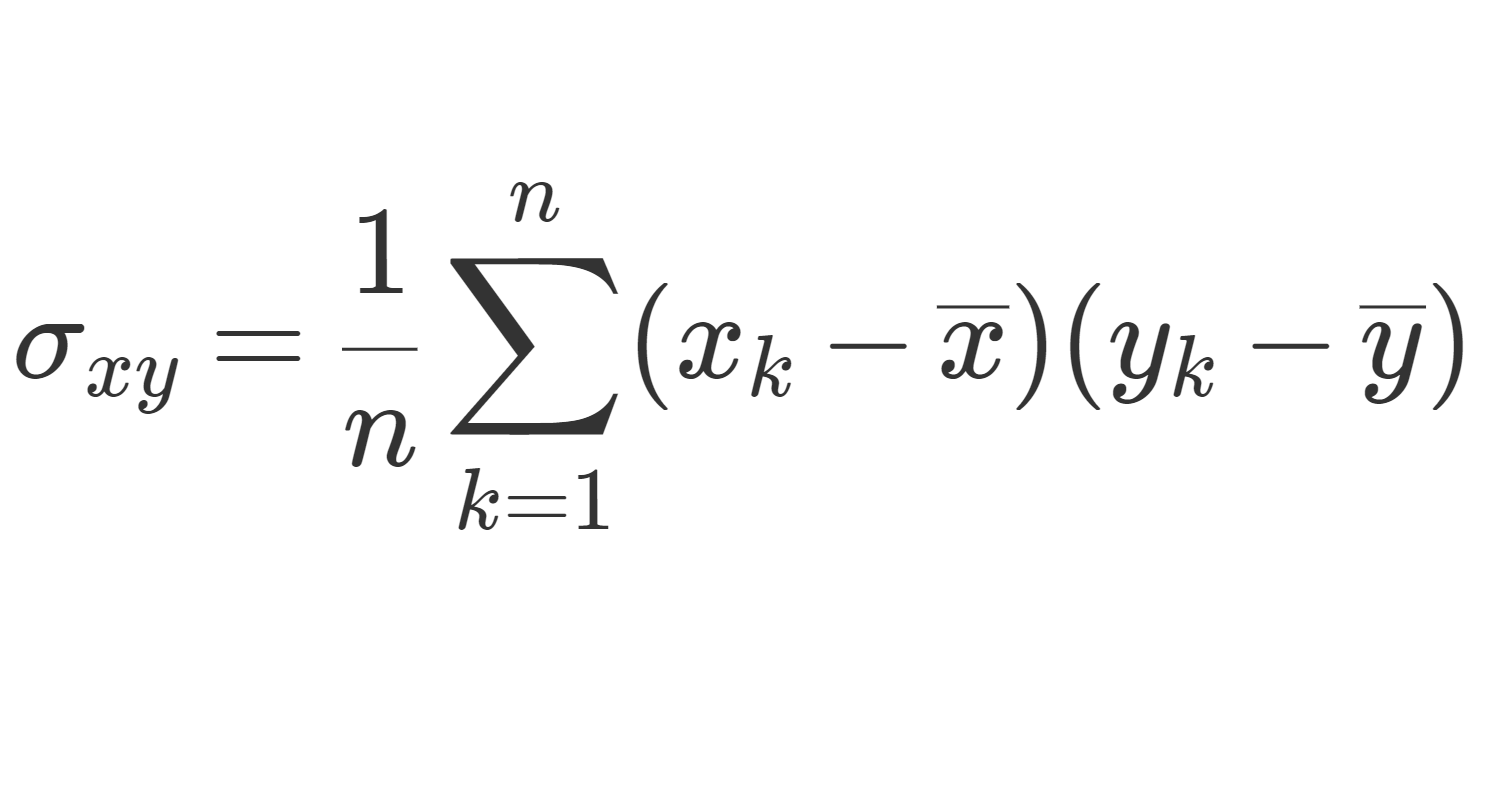統計学における,データの散らばり具合を表す指標である「分散・標準偏差」について,その定義と具体例・大事な性質を紹介します。さらに,分散の定義の「なぜ」についても掘り下げます。
データの分散・標準偏差の定義・具体例・性質まとめ
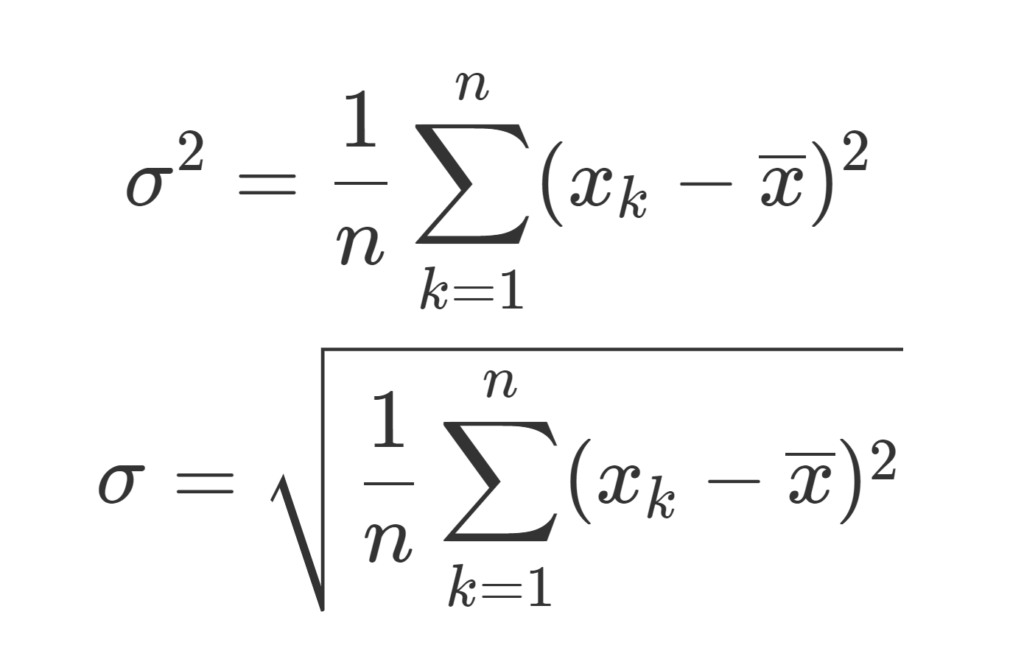
分散・標準偏差はデータの散らばり具合を表す指標です。
データの分散・標準偏差の定義
定義(分散・標準偏差)
データ x_1, x_2, \dots, x_n について,その平均値を \displaystyle\overline{x} = \dfrac{1}{n}\sum_{k=1}^n x_k とする。このとき,
\color{red}\begin{equation}\sigma^2 = \frac{1}{n}\sum_{k=1}^n (x_k-\overline{x})^2\end{equation}
を分散 (variance) といい,
を標準偏差 (standard deviation) という。
分散・標準偏差は \sigma^2, \sigma 以外に \color{red} s^2, s という記号もよく使われる。また,分散は V(x) とかくこともある。
\sigma はギリシャ文字の「シグマ」です。
x_k -\overline{x} を平均値からの偏差 (deviation) といいます。
(1) 式は平均値周りの2乗誤差(偏差の2乗) (x_1-\overline{x})^2,\dots, (x_n-\overline{x})^2 を足してデータ数 n で割っているため,2乗誤差の平均(偏差の2乗の平均)といえますね。したがって,分散は平均値周りの平均2乗誤差 (mean squared error; MSE) とも言えます。
標準偏差は,分散の平方根ですね。2乗した分を平方根取って単位をそろえているんですね。n 次元ユークリッド距離の計算のようです。
定義から当然 \sigma^2 , \sigma \ge 0 ですね。さらに
\sigma^2=0 \iff x_1=x_2=\dots =x_n
も容易にわかるでしょう。すべてが同じ値でない限り,必ず \sigma^2>0 になります。
データの分散・標準偏差の具体例
例1.
データ \color{red} 40, 40, 50, 80,90 の平均は
\overline{x} = \frac{40+40+50+80+90}{5}=60
であるから,分散は
である。標準偏差は \sigma =\sqrt{440}=20.976\cdots である。
普通に計算してあげることで求まりますね。
例2.
データ \color{red} 0, 40, 50, 80,90 の平均は \overline{x}=52,分散は \sigma^2=1016,標準偏差は \sigma=\sqrt{1016}=31.875\cdots である。
さっきはデータ 40,40,50,80,90 だったのを 0,40,50,80,90 にしました。すると平均は 60 から 52 に下がっていますが,それ以上に分散が 440 から 1016 へと大幅に増加しています。
分散は2乗しているが故に,一つでも平均から大きく外れた値があると,その誤差の2乗分が大きく分散にのしかかってくるわけです。これは分散の欠点ですね。
データの分布をヒストグラムにしたものと,分散の大まかな対応を確認しておきましょう。全てデータ数は n=10000 で,平均は 0 になるようにしています。
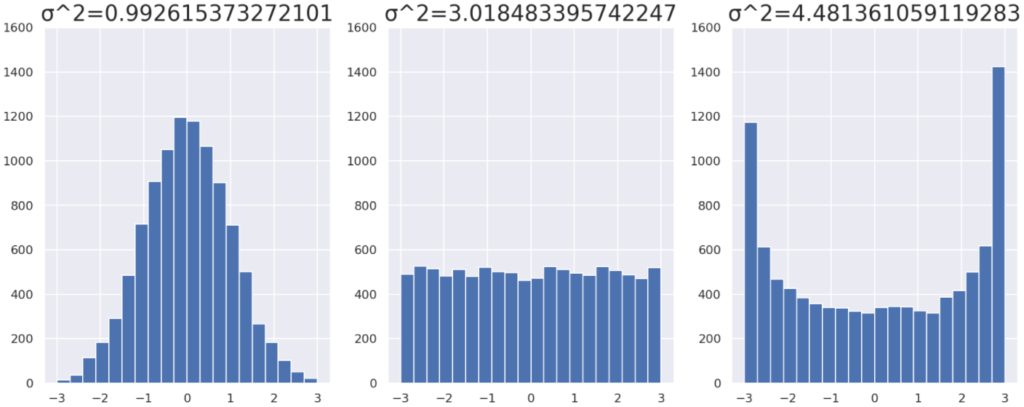
分散がデータの散らばり具合を表しているというのがよくわかりますね。
データの分散・標準偏差の性質
定理(分散・標準偏差の性質)
データ x_1, x_2, \dots, x_n に対し,その平均を \overline{x},分散を \sigma^2,標準偏差を \sigma で表す。このとき,
- \color{red}\sigma^2 = \overline{(x^2)}-(\overline{x})^2.
- \color{red}\overline{x}=\argmin_a \frac{1}{n}\sum_{k=1}^n(x_n-a)^2. すなわち,一般に \frac{1}{n}\sum_{k=1}^n(x_k-a)^2 が最小となる定数 a は, a=\overline{x} である。
\overline{(x^2)} = \frac{1}{n}\sum_{k=1}^n x_k^2 はデータの2乗の平均です。
\argmin の意味は「すなわち」以下にかいてある通りですが,argmax,argminとは~定義と具体例~でも解説しています。
特に1.は大切で,分散は「(2乗の平均)ー(平均の2乗)」で求められるということです。上の具体例を,この公式で求めてみるのは良い練習問題でしょう。
証明
1. \sigma^2 = \overline{(x^2)}-(\overline{x})^2 について
\begin{aligned}\sigma^2&= \frac{1}{n}\sum_{k=1}^n (x_k-\overline{x})^2 \\ &= \frac{1}{n}\sum_{k=1}^n\{ x_k^2-2x_k\overline{x}+ (\overline{x})^2 \}\\ &= \frac{1}{n} \sum_{k=1}^n x_k^2-2\overline{x} \frac{1}{n} \sum_{k=1}^n x_k+ \frac{1}{n} n(\overline{x})^2 \\ &= \overline{(x^2)} -2(\overline{x})^2+ (\overline{x})^2 \\ &= \overline{(x^2)} -(\overline{x})^2 . \end{aligned}
2. \overline{x}=\argmin_a \frac{1}{n}\sum_{k=1}^n(x_k-a)^2 について
であり, a=\overline{x} のとき等号が成立する。よって, a=\overline{x} のとき最小になる。
証明終
変量の変換
\{x_k\}_{k=1}^n の平均・分散・標準偏差をそれぞれ \overline{x}, \sigma^2_x,\sigma_x とし,y_k =ax_k+b としましょう。このときの \{y_k\} の平均・分散・標準偏差 \overline{y}, \sigma^2_y, \sigma_y はそれぞれ
\color{red}\begin{aligned}\overline{y} &= a\overline{x}+b , \\ \sigma_y^2 &= a^2\sigma_x^2,\\ \sigma_y &= |a|\sigma_x \end{aligned}
となることが,計算により分かります。
なぜ2乗した誤差を考えるのか
分散は,平均2乗誤差をもってして散らばり具合を表すものだといいました。ところで,誤差を見るときになぜ2乗するのでしょうか。これについてちょっと考えてみましょう。
2乗せずに和を取っても意味がない
\frac{1}{n} \sum_{k=1}^n (x_k-\overline{x})^2 の代わりに単なる平均誤差
\color{red} \frac{1}{n} \sum_{k=1}^n (x_k-\overline{x})
を考えるとどうなるでしょうか。実は,平均偏差は常に 0 になり,考える意味がありません。実際,
ですね。
絶対値をつけて和をとっても的外れである
それでは,\frac{1}{n} \sum_{k=1}^n (x_k-\overline{x})^2 の代わりに誤差の符号が常に正になるよう,平均絶対誤差 (mean absolute error; MAE)
\color{red}\frac{1}{n} \sum_{k=1}^n |x_k-\overline{x}|を考えるとどうでしょうか(これは平均偏差 (mean absolute deviation) と呼ばれます)。実は,これも以下の点で不都合です。
- 絶対値は関数として解析的(微分可能)でなく,少々扱いづらい。
- \overline{x}\ne \argmin_a \sum_{k=1}^n |x_k-a| である。すなわち,平均絶対誤差を最も最小にするのは a=\overline{x} (平均値周り)ではない。
1. は単に数学的な理由です。四則演算のみでかけている方が,何かと扱いやすいです。
タイトルに「的外れである」と書いたのは2.の理由です。そもそも「誤差」を考えるにあたって,誤差はできるだけ小さくしたいですから,誤差 \frac{1}{n} \sum_{k=1}^n |x_k-a| が最小になるように a の値を定めるのが普通でしょう。上で述べた定理の2.より,分散の定義では,誤差を最小にするのはちゃんと平均値であることを証明しました。
しかし,この平均絶対誤差を最小にする a の値は平均値ではなく,中央値であることが知られています。そもそも平均値周りの誤差を考えるのに,平均絶対誤差は適さないということですね。
逆に,中央値まわりの誤差を考えたいときは,平均絶対誤差を考えるのは有力な候補です。しかし,中央値の導出も四則演算のみでは書けないので,数学的には少々扱いにくいのが難点です。