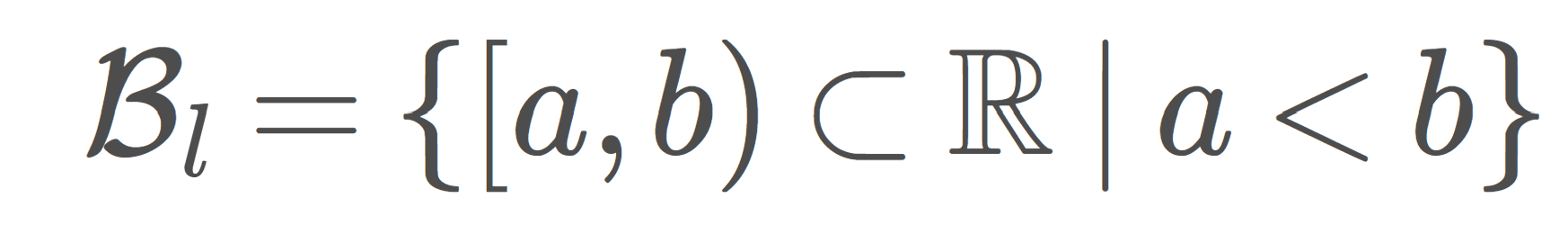【下限位相】ゾルゲンフライ直線について掘り下げる

$\R$ における通常の位相は開区間 $(a,b)$ を開基とする位相ですが，ゾルゲンフライ直線 $\R$ とは半開区間 $[a,b)$ を開基とする位相であり，この位相を下限位相といいます。

ゾルゲンフライ直線は， $\R$ における通常の位相より大きく，通常の位相とは異なった面白い性質をもつものです。性質を掘り下げましょう。

【下限位相】ゾルゲンフライ直線の定義
【下限位相】ゾルゲンフライ直線の性質
関連する記事
参考

【下限位相】ゾルゲンフライ直線の定義

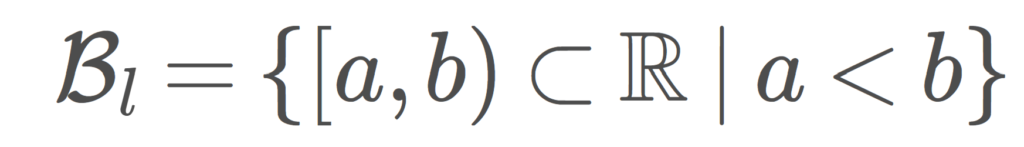
定義（下限位相・ゾルゲンフライ直線）

実数全体の集合 $\R$ に対し，

\Large\color{red} \mathcal{B}_l=\{ [a,b)\subset \R\mid a<b\}

を開基とする位相 $\mathcal{O}_l$ を下限位相 (lower limit topology, right half-open interval topology) といい，位相空間 $(\R, \mathcal{O}_l)$ をゾルゲンフライ直線 (Sorgenfrey line) という。

$\mathcal{B}_l$ を開基とする位相とは，「 $O\subset \R$ が開集合である必要十分条件は， $O$ が $\mathcal{B}_l$ の元となる集合の和集合でかけること」を言います(→開基・準開基と位相の生成について詳しく)。たとえば，

(a,b)=\bigcup_{n\ge 1} \left[a+\frac{1}{n}, b\right)

ですから， $(a,b)\in\mathcal{O}_l$ です。どんな集合が開集合になるか，閉集合になるかを表にしたものが以下です。

$a<b$ とする	$\mathcal{O}_l$ -開集合	$\mathcal{O}_l$ -閉集合
$(a,b)$	〇: $\bigcup_{n\ge 1} [a+1/n, b)$	×
$[a,b]$	×	〇
$[a,b)$	〇	〇
$(a,b]$	×	×
$\{a\}$	×	〇
$(-\infty, b)$	〇: $\bigcup_{n\ge 1} [a-n, b)$	〇
$(-\infty, b]$	×	〇
$(a,\infty)$	〇: $\bigcup_{n\ge 1} [a+1/n, a+n)$	×
$[a, \infty)$	〇: $\bigcup_{n\ge 1} [a, a+n)$	〇

開集合でないことを示すには，開基の次の性質を使います(→開基・準開基と位相の生成について詳しく)。

開基の同値な定義

$(X,\mathcal{O})$ を位相空間とし， $\mathcal{B}\subset \mathcal{O}$ とする。このとき，次は同値である。

$\mathcal{B}$ は開基である
任意の開集合 $O\in\mathcal{O}$ と任意の $x\in O$ について，ある $B_{x}\in \mathcal{B}$ が存在して， $x\in B_{x}\subset O$ とできる。

たとえば， $[a,b]$ が開集合でないときは， $b\in B\subset [a,b]$ となるような $B\in\mathcal{B}_l$ が存在しないからです。

上の表より，直ちに次のことが分かります。

定理1（下限位相は通常の位相より大きい）

$\R$ の通常の位相を $\mathcal{O}$ とすると，下限位相 $\mathcal{O}_l$ は $\mathcal{O}$ より大きい（細かい・強い）。すなわち，

\Large\color{red}\mathcal{O}\subset \mathcal{O}_l

通常の位相は， $\mathcal{B}=\{(a,b)\subset \R\mid a<b\}$ を開基とし， $\mathcal{B}\subset \mathcal{O}_l$ なので分かります。

なお，逆に

\Large\mathcal{B}_u=\{ (a,b]\subset \R\mid a<b\}

を開基とする位相 $\mathcal{O}_u$ を上限位相 (upper limit topology, left half-open interval topology) と言います。同じことなので，本記事では下限位相のみ考えます。

【下限位相】ゾルゲンフライ直線の性質

可算公理・分離公理・コンパクト性・連結性を順番に紹介しましょう。

ゾルゲンフライ直線と可算公理

第一可算	第二可算	可分	距離化可能性
〇	×	〇	×

ゾルゲンフライ直線は，第一可算だが第二可算でない代表的な例の一つです。

証明

第一可算であることについて， $x\in \R$ に対し，

\{ [x, x+q)\mid q\in\mathbb{Q}, \,q>0\}

は基本近傍系をなす可算集合なので，示せた。

第二可算でないことについて， $\mathcal{B}_0\subset \mathcal{O}_l$ を可算開基とすると， $x<y$ に対し， $[x, y)$ は $\mathcal{B}_0$ の元の集合の和集合でかけることになるが， $x\in \R$ の取り方は非可算個あり，全ての $x<y$ でそれが成り立つことはおかしい。よって，第二可算でない。

可分であることについて，有理数全体の集合 $\mathbb{Q}$ は $(\R, \mathcal{O}_l)$ において稠密である。実際，無理数全体の集合に含まれる開基 $\mathcal{B}_l$ は存在しないので，無理数全体の集合の内部(開核)は空集合であるからである。よって，示せた。

距離化可能でないことについて，距離空間では，第二可算と可分は同値であるが，今は可分なのに第二可算でないので，距離化可能でない。

証明終

ゾルゲンフライ直線と分離公理

$T_0, T_1, T_2$ (ハウスドルフ空間)	$T_3$	$T_4,T_5$
〇	〇	〇

本記事では， $T_0$ から $T_5$ は以下のように定義しています。この定義は文献によって変わりますから，注意してください。

名称	定義
$T_0$ コルモゴロフ空間 (Kolmogorov space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ または $x\notin O_y,\, y\in O_y$ となる開集合 $O_y$ の少なくとも一方が取れる
$T_1$	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ と $x\notin O_y, \,y\in O_y$ となる開集合 $O_y$ の両方が取れる
$T_2$ ハウスドルフ空間 (Hausdorff space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset$ となる開集合 $O_x, O_y$ が取れる
$T_3$	任意の閉集合 $F$ と任意の点 $x\in X\setminus F$ に対して， $F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset$ となる開集合 $O_F, O_x$ が取れる
$T_4$	任意の2つの互いに素な空でない閉集合 $F,G\subset X$ に対して， $F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset$ となる開集合 $O_F, O_G$ が取れる
$T_5$	$\overline{A}\cap B=A\cap \overline{B}=\emptyset$ をみたす任意の2つの空でない集合 $A,B\subset X$ に対して， $A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset$ となる開集合 $O_A, O_B$ が取れる

定義から明らかに $T_2\implies T_1\implies T_0$ ， $T_5\implies T_4$ です。

証明

$T_0,T_1, T_2$ であることについて， $\mathcal{O}_l$ は通常の位相 $\mathcal{O}$ より大きく，通常の位相においては， $T_0,T_1, T_2$ であるから，同じくそうである。

$T_3$ であることについて，1点集合 $\{x\}$ は閉集合であることと，後で示すが， $T_4$ であることから，示せた。

$T_4, T_5$ であることについて， $A,B\subset \R$ が，下限位相 $\mathcal{O}_l$ において $\overline{A}\cap B=A\cap \overline{B}=\emptyset$ をみたすとする。このとき， $\R\setminus \overline{B}$ は開集合なので，任意の $a\in \R\setminus \overline{B}$ に対し，ある $x_a\in \R$ が存在して，

[a, x_a) \subset \R\setminus \overline{A}

とできる。ここで，

O_A = \bigcup_{a\in A} [a, x_a) \supset A

とすると，これは開集合である。 $O_B\supset B$ も同様に定めるとする。このとき， $O_A\cap O_B=\emptyset$ である。実際，そうでないとすると，ある $a\in A,\, b\in B$ に対し， $[a, x_a)\cap [b, x_b)\ne\emptyset$ となる。もし， $a<b$ とすると， $b\in [a, x_a)\subset \R\setminus\overline{B}$ となり， $a>b$ とすると， $a\in [b, x_b)\subset \R\setminus \overline{A}$ となる。いずれにしろ矛盾している。

したがって， $O_A\cap O_B=\emptyset$ が言えたので， $T_5$ が示せた。よって $T_4$ でもある。

証明終

$T_1$ かつ $T_5$ が成り立つことを完全正規 (completely normal) ということがあります。

ゾルゲンフライ直線とコンパクト性

コンパクト	点列コンパクト	σコンパクト	局所コンパクト	リンデレーフ	パラコンパクト
×	×	×	×	〇	〇

$\R$ は通常の位相でもコンパクトではありませんが， $[0,1]$ は通常の位相でコンパクトです。一方で，ゾルゲンフライ直線においては， $[0,1]$ もコンパクトではありません。

コンパクトでないこと，σコンパクトでないこと，局所コンパクトでないことは，以下の定理から直ちにわかります。

定理（ゾルゲンフライ直線におけるコンパクト集合）

ゾルゲンフライ直線 $(\R, \mathcal{O}_l)$ において， $A\subset X$ がコンパクトならば， $A$ は高々可算集合で，かつ $A$ の通常の位相における内部(開核)が空集合である。

たとえば， $\{ 1/n\mid n\ge 1\}\cup \{0\}$ はコンパクトです。

「通常の位相における内部(開核)が空集合である」の部分は，「 $A$ は通常の位相における疎集合 (nowhere dense) である」といってもよいです。疎集合の厳密な定義は， $A$ の閉包の内部(開核)が空集合であること，すなわち， $\operatorname{Int}(\overline{A})=\emptyset$ ですが，ハウスドルフ空間 ( $T_2$ 空間) におけるコンパクト集合は閉集合であることから，今は同じことです。

なお，逆に高々可算集合かつ疎集合 (nowhere dense) だからといって，コンパクトとは言えません。たとえば， $\mathbb{Z}\subset \R$ はコンパクトではありません。

ゾルゲンフライ直線が点列コンパクトでないことは，数列 $1,2,3,\ldots,$ が収束しないことから分かります。

定理の証明

$A\subset X$ をコンパクトとする。このとき，任意の $a\in A$ に対して，ある $x_a<a$ が存在して， $(x_a, a)\cap A=\emptyset$ とできることを示そう。

もしある $a\in A$ で，そうでないとすると， $\{a_n\}\subset A$ が上昇列(増大列)でかつ $a_n \xrightarrow{n\to\infty} a$ となるものが取れる。このとき，

(-\infty, a_1) \cup \bigcup_{n=1}^\infty [a_n, a_{n+1}) \cup [a, \infty)

は $A$ の開被覆となるが，有限部分被覆が存在しないので， $A$ のコンパクト性に矛盾する。よって赤字は示せた。

赤字により， $A$ の通常の位相における内部(開核)が空集合であることが直ちにわかる。また， $n\ge 1$ に対し， $A_{m, n}=\{ a\in A\cap [m,m+1] \mid a-x_a>1/n\}$ は高々 $n$ 個以下の集合であり，

A = \bigcup_{m, n =1}^\infty A_{m, n}

なので， $A$ は高々可算集合である。

証明終

最後に，リンデレーフであることと，パラコンパクトであることを示しましょう。

リンデレーフ・パラコンパクトであることの証明

リンデレーフであることについて

$\{U_\lambda\}_{\lambda\in\Lambda}\subset \mathcal{O}_l$ を $\R$ の開被覆とする。 $\mathcal{O}$ を $\R$ における通常の位相とする。 $\lambda\in\Lambda$ に対し，

O_\lambda = \operatorname{Int}_{\mathcal{O}}(U_\lambda)

と定める。すなわち， $O_\lambda$ は， $U_\lambda \in\mathcal{O}_l$ の通常の位相 $\mathcal{O}$ における内部(開核)と定める。 $O=\bigcup_{\lambda\in\Lambda} O_\lambda$ とおくと， $O\subset \R$ は $\mathcal{O}$ -開集合である。 $\R$ の任意の $\mathcal{O}$ -開集合はリンデレーフであるから，ある可算開部分被覆 $\{O_n\}_n\subset \{O_\lambda\}_{\lambda\in\Lambda}$ が存在して，

O=\bigcup_n O_n

とかける。さらに， $A=\R\setminus O$ は高々可算集合であることを示そう。 $a\in A$ に対し，ある $a<x_a$ が存在して， $(a,x_a)\cap A=\emptyset$ とできる。実際， $a\in U_\lambda$ となる $\lambda\in \Lambda$ を取ると，開基の定義より，