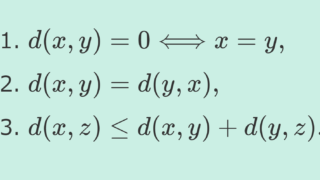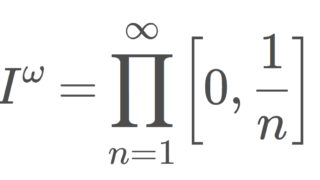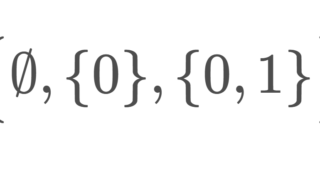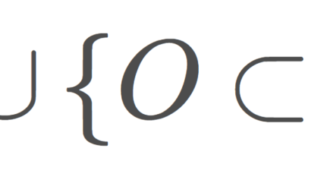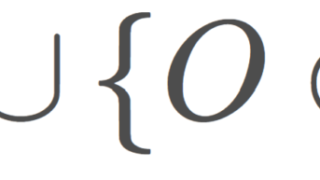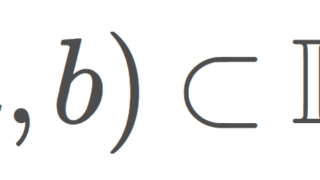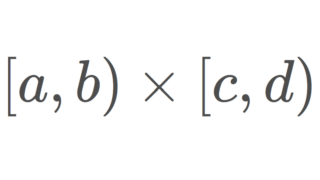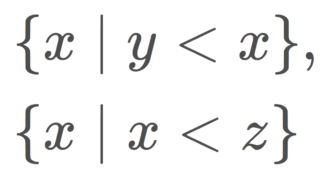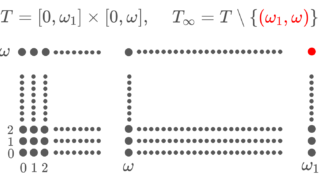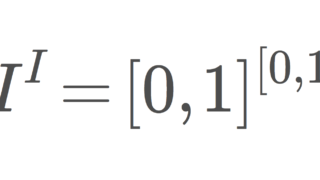本サイトにおいて,1記事を割いて紹介している,さまざまな具体的な位相空間をまとめます。位相空間の定義は,位相空間の定義と開集合・閉集合についてを参照してください。
頻出で基本的な位相空間
1. 密着空間
空でない集合 X に対し,\mathcal{O}=\{ \emptyset, X\} と定めると, \mathcal{O} は位相空間となる。これを密着位相 (indiscrete topology, trivial topology) といい, (X, \mathcal{O}) を密着空間 (indiscrete space, trivial space) という。
密着空間は1記事割いているわけではないですが,基本的な位相空間です。
2. 離散空間
空でない集合 X に対し,\mathcal{O}=2^X ( X のべき集合)と定めると, \mathcal{O} は位相空間となる。これを離散位相 (discrete topology) といい, (X, \mathcal{O}) を離散空間 (discrete space) という。
離散空間は1記事割いているわけではないですが,基本的な位相空間です。
3. 距離空間
X を空でない集合とする。関数 d\colon X \times X \to [0, \infty) が以下の性質をみたすとき,距離関数 (distance function) という。
- d(x, y) = 0 \Longleftrightarrow x = y,
- d(x, y) = d(y, x),
- d(x,z) \le d(x, y) + d(y, z). (三角不等式)
このとき, (X, d) ,または単に X は距離空間 (metric space) であるという。
距離空間のみたす位相的性質については,またいずれ別の記事で紹介したいと思います。
4. ノルム空間・内積空間・バナッハ空間・ヒルベルト空間
距離空間かつベクトル空間の一種です。それぞれ以下の記事で解説しています。
その他の具体的な位相空間
ここからは,特筆すべき性質も一緒に紹介していきます。
5. ヒルベルト立方体
n\ge 1 に対し,通常の位相が入った閉区間 [0,1/n] の直積位相空間
I^\omega = \prod_{n=1}^\infty \left[ 0,\frac{1}{n}\right]
をヒルベルト立方体 (Hilbert cube) という。
距離空間の一種です。つまり,距離化可能です。
6. シェルピンスキー空間
2点集合 S=\{0,1\} について,その上の開集合族を
\mathcal{O}=\Bigl\{ \emptyset, \{0\}, \{0,1\}\Bigr\}
としたときの位相空間 (S,\mathcal{O}) をシェルピンスキー空間 (Sierpinski space) という。
ただの2点集合ですが,基本的で面白い性質をもちます。
7. 特定点位相
X を空でない集合とし, p\in X とする。
\mathcal{O}_p =\{\emptyset\}\cup \{ O\subset X\mid p\in O\}
を, p を含む部分集合全体の集合(と空集合の和集合)とすると,(X,\mathcal{O}_p) は位相空間となる。この位相を特定点位相 (particular point topology) という。
以下の表では, X は無限集合とします。
| 可算公理 | X が非可算のときは第一可算・可分だが第二可算でない |
| 分離公理 | T_0 空間だが T_1, T_2, T_3, T_4, T_5 でない |
| コンパクト性 | コンパクト・点列コンパクトでないが,局所コンパクトである |
| 連結性 | 連結・局所連結・弧状連結 |
また,特定点位相は,可分空間の部分空間が可分でない例や,コンパクトだが相対コンパクトでない例を作るのにも使えます。
8. 除外点位相
X を空でない集合とし, p\in X とする。
\mathcal{O}_{\neg p} =\{X\}\cup \{ O\subset X\mid p\notin O\}
を, p を含まない部分集合全体の集合(と全体集合の和集合)とすると,(X,\mathcal{O}_{\neg p}) は位相空間となる。この位相を除外点位相 (excluded point topology) という。
以下の表では, X は無限集合とします。
| 可算公理 | X が非可算のときは第一可算だが第二可算・可分でない |
| 分離公理 | T_0, T_4, T_5 空間だが T_1, T_2, T_3 でない |
| コンパクト性 | コンパクト・点列コンパクト |
| 連結性 | 連結・局所連結・弧状連結 |
9. 補有限位相
X を空でない集合とする。
\mathcal{O}_f=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\}
を,補集合が有限集合である部分集合全体(と \{\emptyset\} との和集合)とすると, (X,\mathcal{O}_f) は位相空間になる。この位相を補有限位相 (cofinite topology, finite complement topology) という。
以下の表で, X は無限集合とします。
| 可算公理 | X が非可算なら可分だが第一可算・第二可算でない |
| 分離公理 | T_0, T_1 空間だが T_2, T_3, T_4, T_5 でない |
| コンパクト性 | コンパクト・点列コンパクト |
| 連結性 | 連結・局所連結 X が可算なら弧状連結でないが,非可算なら弧状連結 |
10. 補可算位相
X を空でない集合とする。
\mathcal{O}_c=\{\emptyset \}\cup \left\{O\subset X\middle|\begin{gathered} X\setminus O \text{ is at most} \\ \text{countable}\end{gathered}\right\}
を,補集合が高々可算集合である部分集合全体(と \{\emptyset\} との和集合)とすると, (X,\mathcal{O}_c) は位相空間になる。この位相を補可算位相 (cocountable topology, countable complement topology) という。
以下で, X は非可算とします。
| 可算公理 | 第一可算・第二可算・可分いずれも不成立 |
| 分離公理 | T_0, T_1 空間だが T_2, T_3, T_4, T_5 でない |
| コンパクト性 | コンパクト・点列コンパクト・局所コンパクトいずれも不成立だが,リンデレーフではある |
| 連結性 | 連結・局所連結だが弧状連結でない |
11. 補コンパクト位相
(\R,\mathcal{O}) を実数全体の集合における,通常の位相空間とする。
\mathcal{O}_{cc} =\{ \emptyset\}\cup \{ O\subset \R\mid \R\setminus O \text{ is }\mathcal{O}\text{-compact}\}
を,補集合が (\R,\mathcal{O}) におけるコンパクト集合になる部分集合全体(と \emptyset の和集合)とすると,(\R,\mathcal{O}_{cc}) は位相空間になる。これを,補コンパクト位相 (compact complement topology) という。
補コンパクト位相は, \R 上の補有限位相より大きく,通常の位相より小さな位相です。
12. ゾルゲンフライ直線(下限位相)
実数全体の集合 \R に対し,
\mathcal{B}_l=\{ [a,b)\subset \R\mid a<b\}
を開基とする位相 \mathcal{O}_l を下限位相 (lower limit topology, right half-open interval topology) といい,位相空間 (\R, \mathcal{O}_l) をゾルゲンフライ直線 (Sorgenfrey line) という。
下限位相は,通常の位相より大きな位相です。
13. ゾルゲンフライ平面
(\R, \mathcal{O}_l) をゾルゲンフライ直線とするとき,その直積位相空間 (\R, \mathcal{O}_l)\times (\R, \mathcal{O}_l) をゾルゲンフライ平面 (Sorgenfrey plane) という。
| 可算公理 | 第一可算・可分だが第二可算でない |
| 分離公理 | T_0, T_1,T_2, T_3 空間だが T_4, T_5 でない |
| コンパクト性 | 局所コンパクト・σコンパクト・リンデレーフ・パラコンパクト・メタコンパクトいずれでもない |
| 連結性 | 完全不連結 |
ゾルゲンフライ平面は,リンデレーフ空間の直積はリンデレーフでない例になっています。これは,コンパクト空間の直積がコンパクトになるチコノフの定理とは対照的です。また, T_0 から T_3 までは,元の空間が T_i ならば直積空間も T_i だといえますが, T_4, T_5 は,直積空間が T_4, T_5 になるとは言えません。特に,正則空間 (regular space) の直積は正則ですが,正規空間 (normal space) の直積は正規とは言えません。そのような例にもなっています。
14. K位相(スミルノフ位相)
K= \{ 1/n\mid n=1,2,3,\ldots\} とする。実数の集合 \R において,
\mathcal{B}_K = \{ (a,b)\mid a<b\}\cup \{(a,b)\setminus K\mid a<b\}
を開基とする位相 \mathcal{O}_K をK位相 (K-topology) またはスミルノフ位相 (Smirnov’s deleted sequence topology) という。\R における通常の位相を \mathcal{O} とすると,
\mathcal{O}_K = \{ O\setminus L\mid O\in\mathcal{O},\, L\subset K\}
と表せる。
K位相は,通常の位相より大きな位相です。
| 可算公理 | 第一可算・第二可算・可分 |
| 分離公理 | T_0, T_1,T_2 空間だが T_3, T_4, T_5 でない |
| コンパクト性 | 局所コンパクト・点列コンパクトでないが,σコンパクト・リンデレーフである 可算パラコンパクトでないが,メタコンパクトである |
| 連結性 | 連結だが,局所連結・弧状連結でない |
15. 位相幾何学者の正弦曲線
\R^2 の部分集合
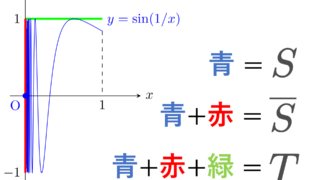
S=\left\{\left(x, \sin\frac{1}{x}\right)\middle| 0<x\le 1\right\}\cup \{(0,0)\}
に, \R^2 から定まる相対位相を入れた部分位相空間 S を位相幾何学者の正弦曲線 (Topologist’s sine curve) という。また, S の \R^2 における閉包
\overline{S} = S\cup \left(\{0\}\times [-1,1]\right)
を閉じた位相幾何学者の正弦曲線 (closed Topologist’s sine curve) という。さらに,
T=\overline{S}\cup \left([0,1]\times \{1\}\right)
を拡張された位相幾何学者の正弦曲線 (extended Topologist’s sine curve) という。
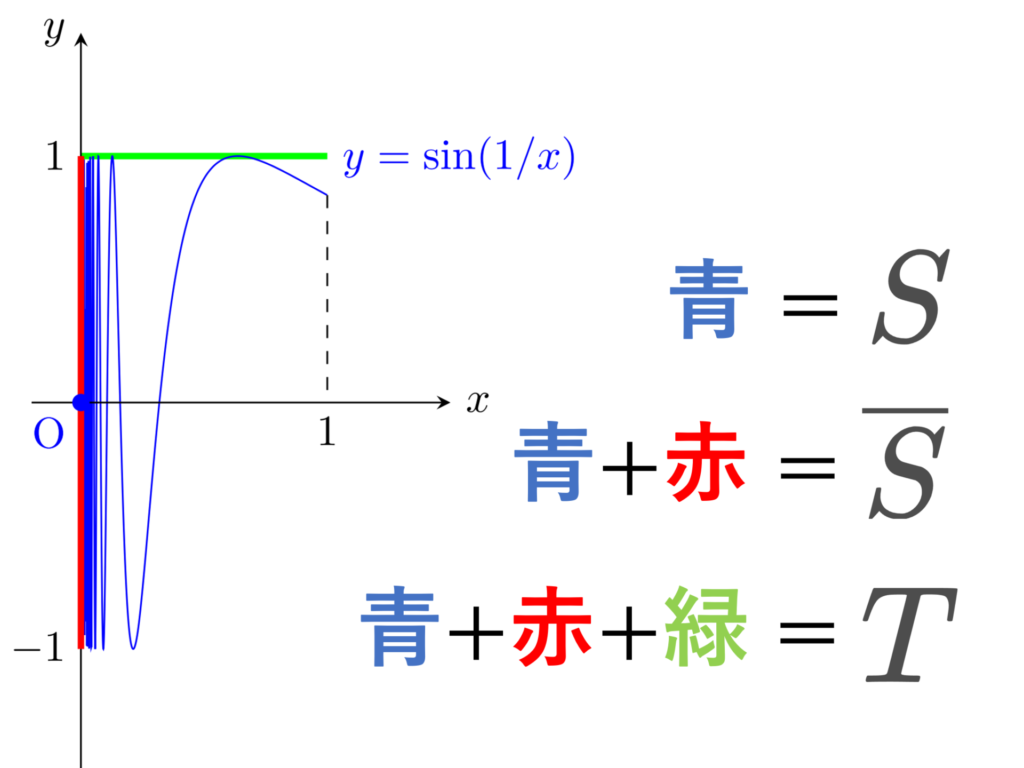
通常の正弦曲線 y=\sin x ではなく, y=\sin(1/x) をベースにしています。
| 可算公理 | 第一可算・第二可算・可分 |
| 分離公理 | T_0 から T_5 まですべて成立 |
| コンパクト性 | S はコンパクトでも点列コンパクトでもない \overline{S}, T はコンパクトかつ点列コンパクト |
| 連結性 | S, \overline{S} は連結だが弧状連結・局所連結でない T は連結・弧状連結だが局所連結でない |
16. くし空間
a\in \R に対し, \R^2 における部分集合を I_a =\{a\}\times [0,1]=\{(a, y)\mid 0\le y\le 1\} とする。
C =I_0\cup \left(\bigcup_{n=1}^\infty I_{1/n}\right) \cup ([0,1]\times\{0\})
に \R^2 から定まる相対位相を入れた位相空間をくし空間 (comb space) という。また, C\setminus\{(0,0)\} を,原点を除いたくし空間という。
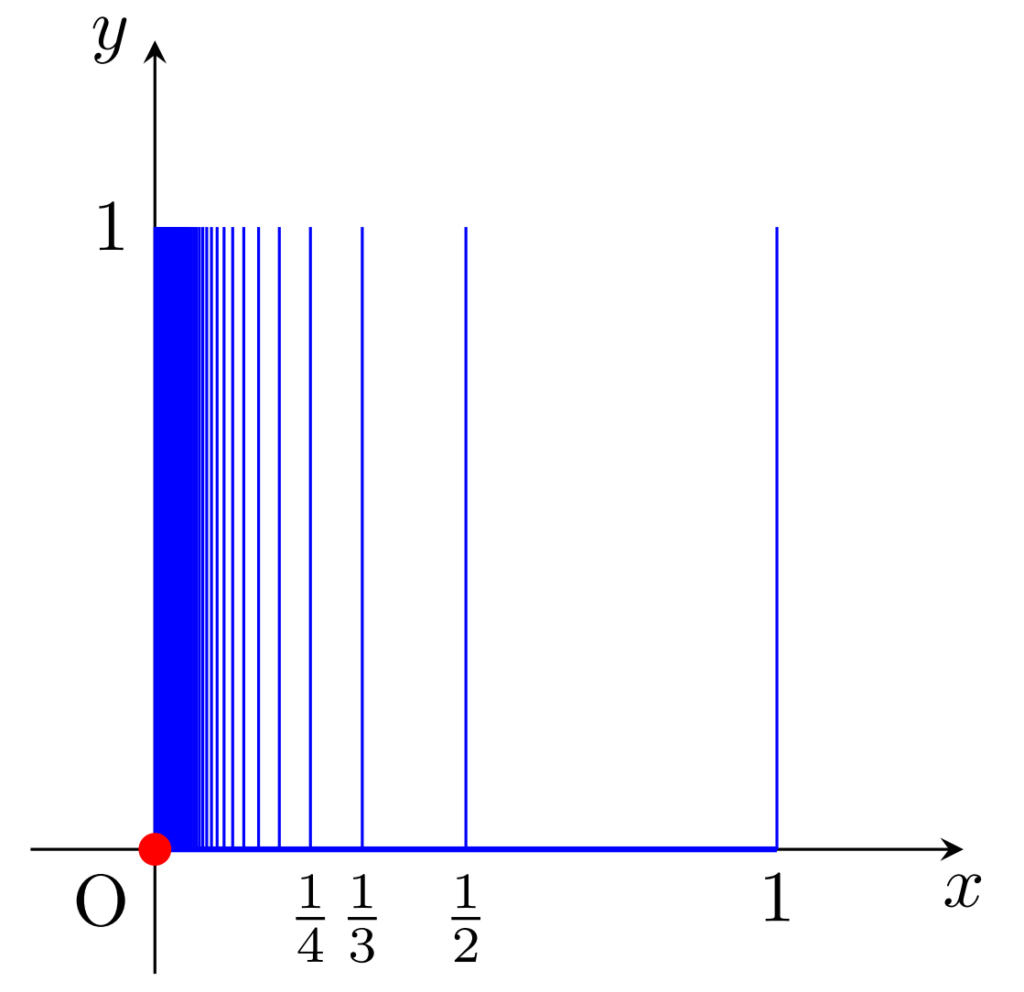
| 可算公理 | 第一可算・第二可算・可分 |
| 分離公理 | T_0 から T_5 まですべて成立 |
| コンパクト性 | C はコンパクトかつ点列コンパクト C\setminus \{(0,0)\} はコンパクトでも点列コンパクトでもない |
| 連結性 | C は連結・弧状連結だが局所連結でない C\setminus \{(0,0)\} は連結だが弧状連結・局所連結でない |
17. ほうき空間
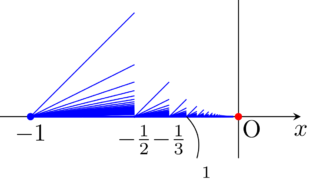
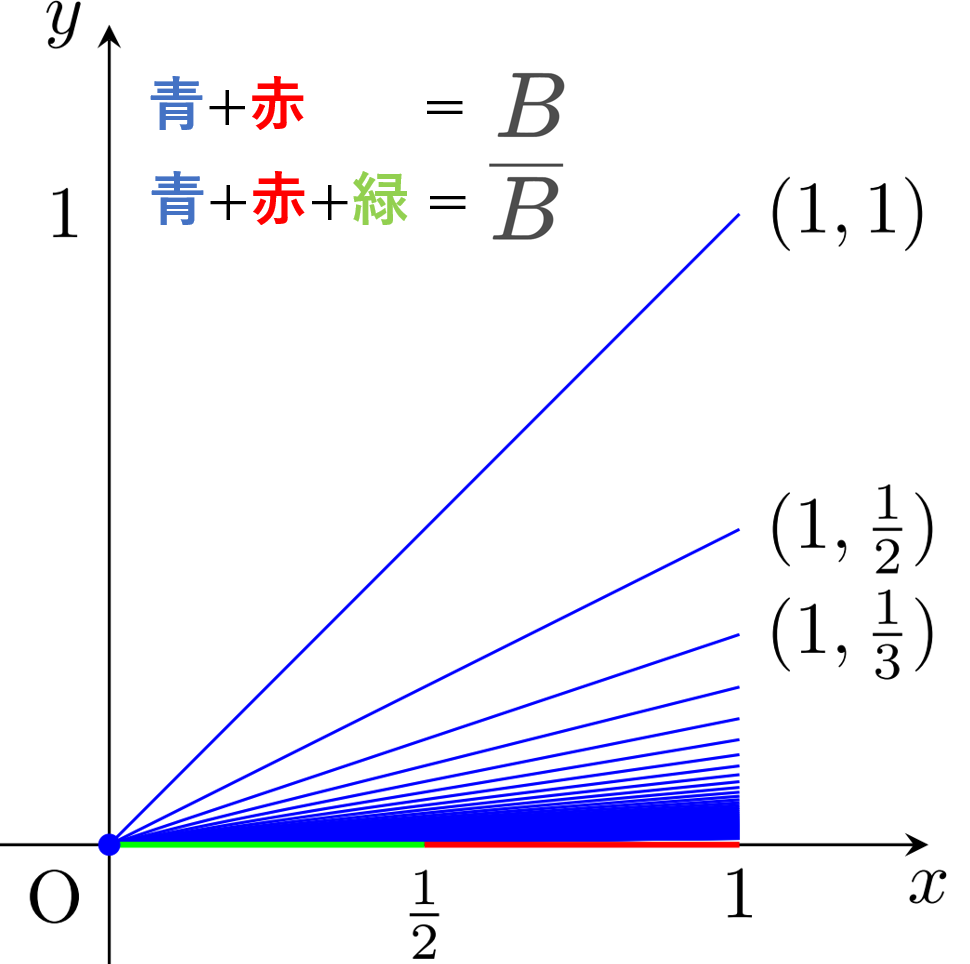
\R^2 において,原点と点 (1,1/n) を結んだ線分(端点含む)を I_{1/n} とかき,
B=\left(\bigcup_{n=1}^\infty I_{1/n}\right) \cup \Bigl( (1/2,1]\times \{0\}\Bigr)
を考える。位相空間 B\subset \R^2 をほうき空間 (infinite broom, broom space) という。また,その閉包 \overline{B}=B\cup ([0,1/2]\times \{0\}) を閉ほうき空間 (closed infinite broom, closed broom space) という。
| 可算公理 | 第一可算・第二可算・可分 |
| 分離公理 | T_0 から T_5 まですべて成立 |
| コンパクト性 | B はコンパクトでも点列コンパクトでもない \overline{B} はコンパクトかつ点列コンパクト |
| 連結性 | B は連結だが弧状連結・局所連結でない \overline{B} は連結・弧状連結だが局所連結でない |
ほうき空間のそのものも大事ですが,ほうき空間を無限個繋ぎ合わせた空間も面白いです。以下で解説しています。
18. 順序位相
X を全順序集合とする。このとき,各 y,z\in X に対して,
\{ x\mid y<x\},\quad \{ x\mid x<z\}
の形の集合たちを準開基とする位相を順序位相 (order topology) という。
たとえば,\R における順序位相は通常の位相と一致します。
以下では,順序数における順序位相を考えます。 \omega_1 を最小の非可算順序数とし,\omega_1=[0,\omega_1) と \omega_1+1= [0,\omega_1] について考えます。
| 可算公理 | [0,\omega_1) は第一可算だが第二可算・可分でない [0,\omega_1] は第一可算でも第二可算でも可分でもない |
| 分離公理 | T_0 から T_5 まですべて成立 |
| コンパクト性 | [0,\omega_1) はコンパクトでないが,点列コンパクトではある [0,\omega_1] はコンパクトかつ点列コンパクトである |
| 連結性 | 完全不連結 |
19. 実数における右順序位相
\R の部分集合族について,
\mathcal{O}_r =\{\emptyset, \R\}\cup \{ (a,\infty)\mid a\in\R \}
と定めると, (\R, \mathcal{O}_r) は位相空間になる。この位相を右順序位相 (right order topology) またはスコット位相 (Scott topology) という。
| 可算公理 | 第一可算・第二可算・可分 |
| 分離公理 | T_0, T_4,T_5 空間だが T_1, T_2, T_3 でない |
| コンパクト性 | コンパクト・点列コンパクトでないが,σコンパクト・リンデレーフである |
| 連結性 | 連結・局所連結・弧状連結 |
20. 長い直線
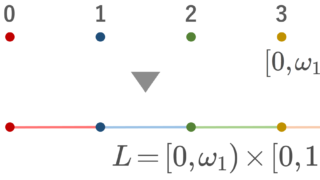
L= [0,\omega_1)\times [0,1) において,辞書式順序による順序位相を入れた位相空間を考える。これを長い直線 (long line) またはアレキサンドロフ直線 (Alexandroff line) という,
また, L に最大元を加えた L^* =L\cup \{\omega_1\} を拡張された長い直線 (extended long line) という。
長い直線は,局所的には通常の直線と同じ振る舞いをしますが,普通の直線より圧倒的に長いです。
| 可算公理 | L は第一可算だが第二可算・可分でない L^* は第一可算でも第二可算でも可分でもない |
| 分離公理 | T_0 から T_5 まですべて成立 |
| コンパクト性 | L はコンパクトでないが,点列コンパクトではある L^* はコンパクトかつ点列コンパクトである |
| 連結性 | L は連結・局所連結・弧状連結である L^* は連結・局所連結だが,弧状連結でない |
21. チコノフの板
直積空間 T= [0,\omega_1]\times [0,\omega] をチコノフの板 (Tychonoff plank) という。また, T_\infty =T\setminus \{(\omega_1,\omega)\} を欠けたチコノフの板 (deleted Tychonoff plank) という。
| 可算公理 | 第一可算・第二可算・可分いずれも不成立 |
| 分離公理 | T は T_0,T_1,T_2, T_3, T_4 だが T_5 でない T_\infty は T_0,T_1,T_2, T_3 だが T_4, T_5 でない |
| コンパクト性 | T はコンパクト・点列コンパクト・局所コンパクト T_\infty はコンパクト・点列コンパクト・極限点コンパクトでないが,擬コンパクト・局所コンパクトである |
| 連結性 | 完全不連結 |
22. I^I
I=[0,1] を単位区間とし, I^I に入る直積位相を考えます。
| 可算公理 | 第一可算・第二可算でないが,可分である |
| 分離公理 | T_0, T_1,T_2,T_3, T_4 空間だが T_5 でない |
| コンパクト性 | コンパクトだが,点列コンパクトでない |
| 連結性 | 連結・局所連結・弧状連結 |
I^I は,コンパクトだが点列コンパクトでない例として有名です。
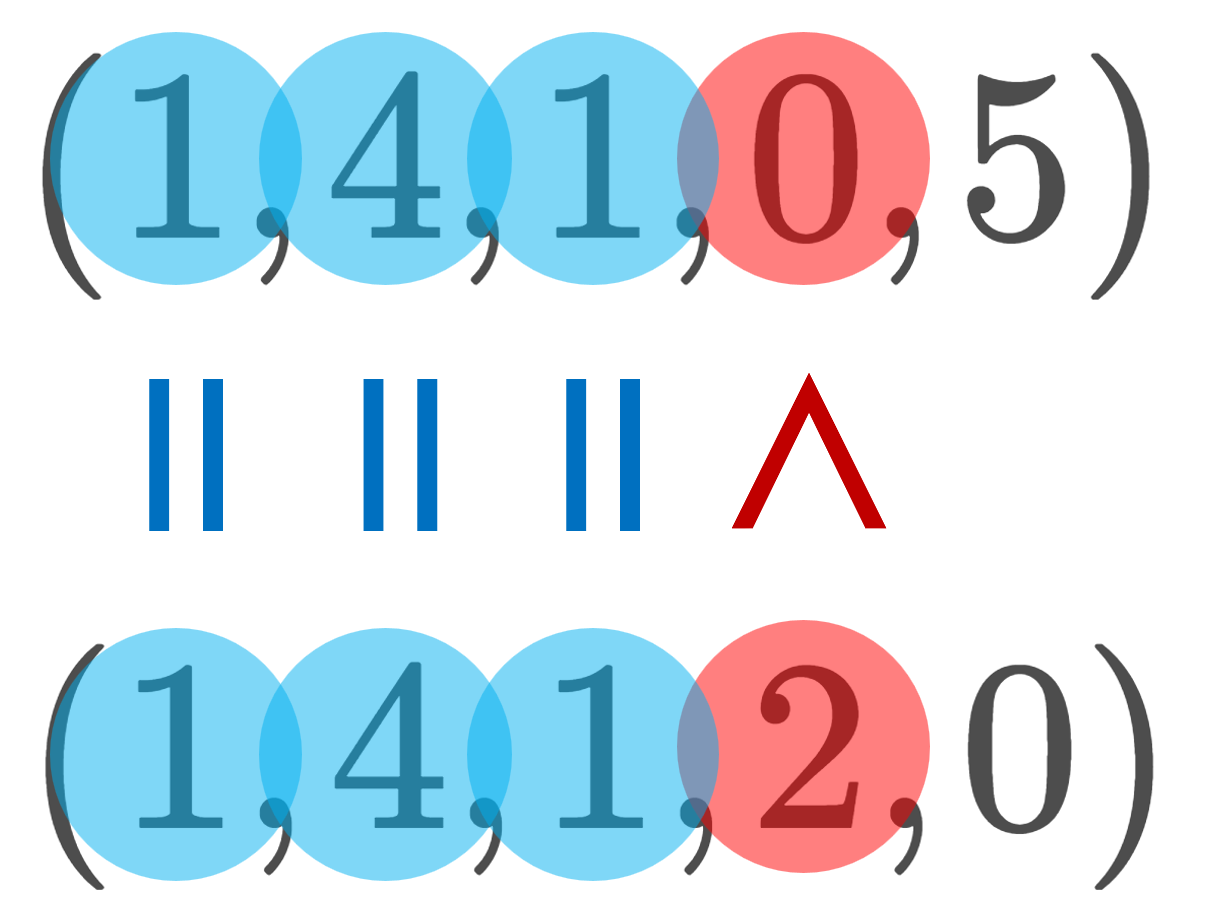
23. Irrational Slope Topology
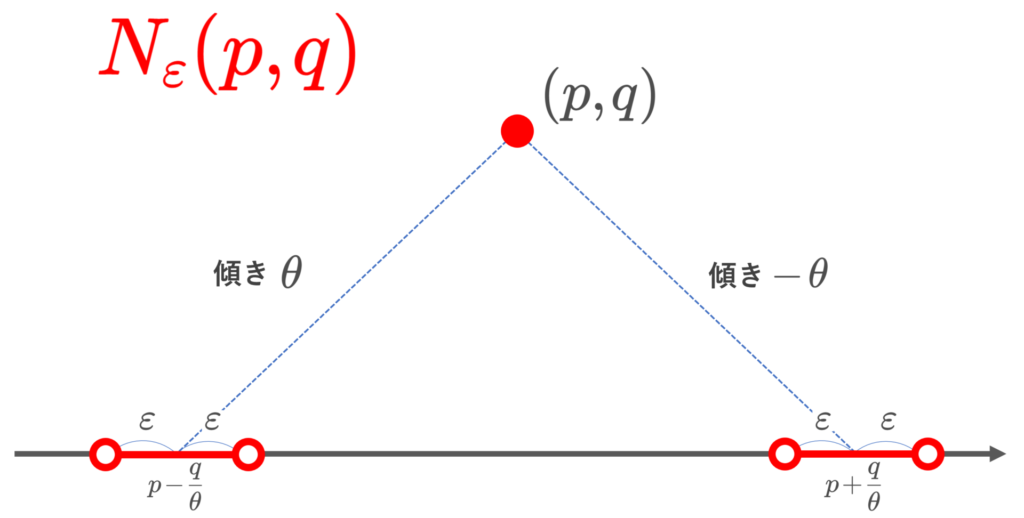
X = \{ (p,q)\in \mathbb{Q}^2\mid q\ge 0\} とする。さらに,無理数 \theta>0 を一つ固定する。 (p,q)\in X に対し,その \varepsilon -近傍 (\varepsilon>0) を
\begin{aligned} &N_\varepsilon (p,q)\\&=\{(p,q)\}\cup B_\varepsilon \left(p+\frac{q}{\theta}\right) \cup B_\varepsilon \left(p-\frac{q}{\theta}\right) \end{aligned}
と定める。ただし, x\in\mathbb{R} に対し, B_\varepsilon(x) =\{ (r,0)\in\mathbb{Q}^2\mid |r-x|<\varepsilon\} である。N_\varepsilon によって生成される位相 \mathcal{O} を Irrational slope topology という。
| 可算公理 | 第一可算・第二可算・可分 |
| 分離公理 | T_0, T_1,T_2 空間だが T_{2\frac{1}{2}},T_3,T_{3\frac{1}{2}},T_4, T_5 でない |
| コンパクト性 | コンパクト・点列コンパクト・可算コンパクトでないが,σコンパクト・リンデレーフ・擬コンパクト・局所コンパクトである |
| 連結性 | 連結だが弧状連結でない |
最後に
まだまだ位相空間はたくさんありますから,今後も追記していきたいと思います。