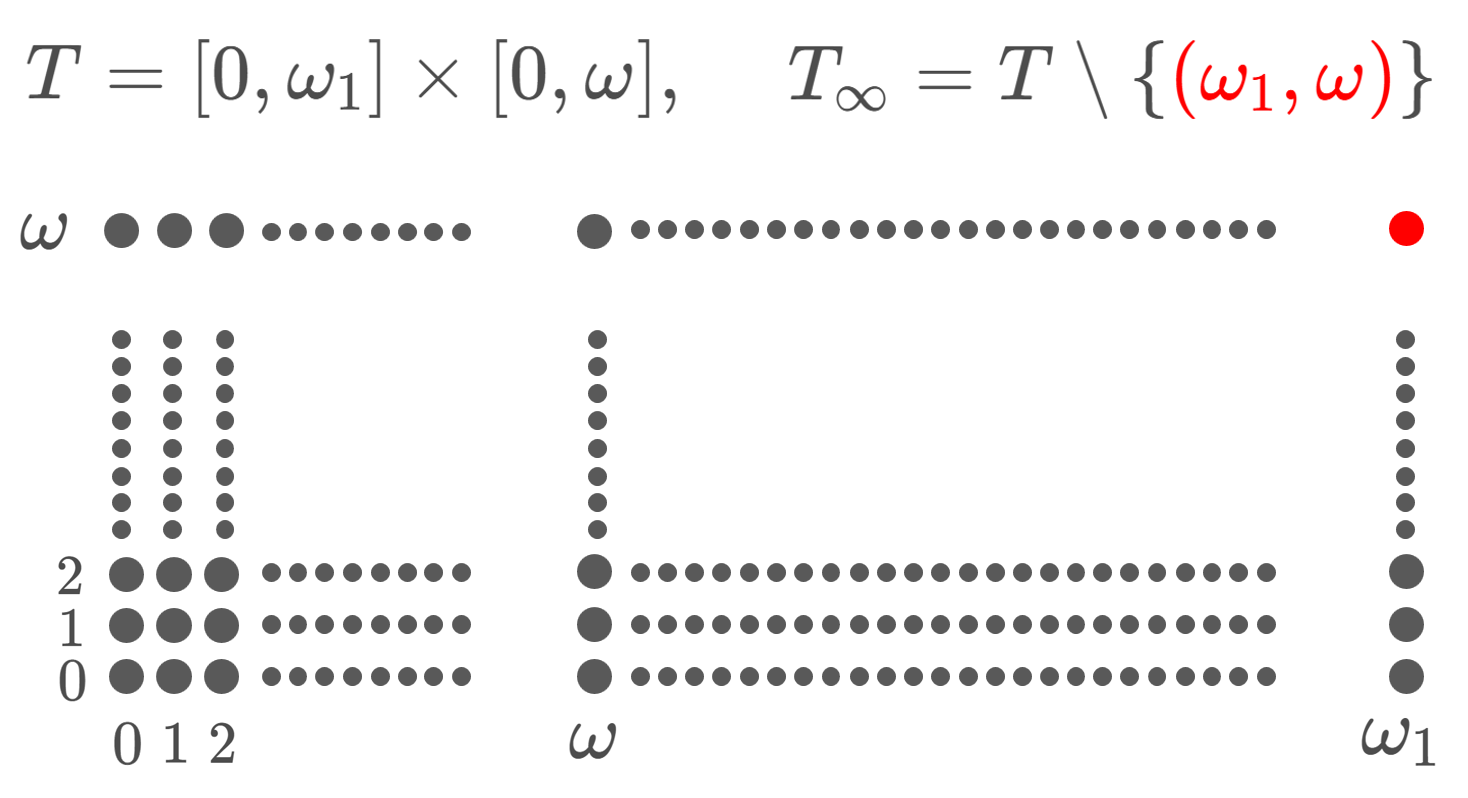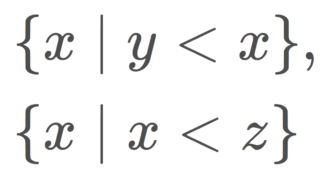チコノフの板とは,順序位相の直積空間であり, T_4 だが T_5 でない空間の例として,あるいは正規だが completely 正規でない空間の例として紹介されます。
チコノフの板について,その位相的性質を解説しましょう。
チコノフの板
以下で, \omega を最小の極限順序数, \omega_1 を最小の非可算順序数とし, [0,\omega]=\{0,1,2,\ldots, \omega\},\, [0,\omega_1]= \{0,1,2,\ldots, \omega_1\} とします。また, [0,\omega],[0,\omega_1] には順序位相が入っているとします。
定義(チコノフの板)
直積空間 \large \color{red}T= [0,\omega_1]\times [0,\omega] をチコノフの板 (Tychonoff plank) という。また, \large\color{red} T_\infty =T\setminus \{(\omega_1,\omega)\} を欠けたチコノフの板 (deleted Tychonoff plank) という。
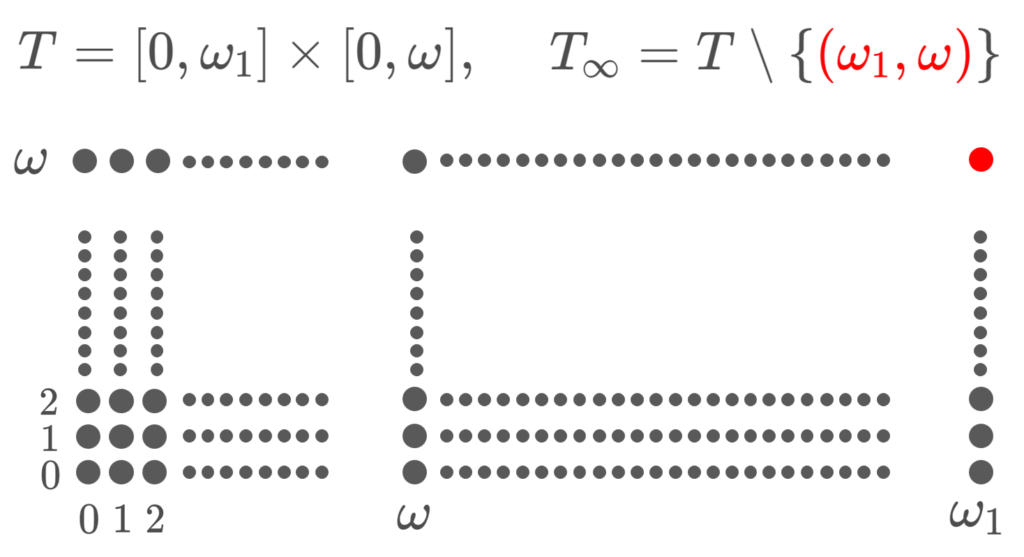
単純に順序位相空間 [0,\omega_1] と [0,\omega] の直積をチコノフの板と呼んでいるんですね。というのも,位相的に面白いからです。見ていきましょう。
チコノフの板の位相的性質
まずは取り上げる性質をまとめます。
| T | T_\infty | |
|---|---|---|
| 第一可算・第二可算・可分・距離化可能 | × | × |
| T_0, T_1, T_2, T_3 空間 | 〇 | 〇 |
| T_4 空間 | 〇 | × |
| T_5 空間 | × | × |
| コンパクト | 〇 | × |
| 極限点コンパクト | 〇 | × |
| 擬コンパクト | 〇 | 〇 |
| 局所コンパクト | 〇 | 〇 |
| 完全不連結 | 〇 | 〇 |
チコノフの板は, T_4 だが T_5 でない空間の例としてよく挙げられます。見ていきましょう。
チコノフの板と可算公理
T, T_\infty が第一可算・第二可算でないこと,可分でないことは, [0,\omega_1] がそうでないことから分かります。距離化可能なら第一可算でなければならないので,距離化可能ではありません。
チコノフの板と分離公理
| T | T_\infty | |
|---|---|---|
| T_0, T_1, T_2, T_3 空間 | 〇 | 〇 |
| T_4 空間 | 〇 | × |
| T_5 空間 | × | × |
分離公理は,本サイトでは以下の定義を採用しています。これは文献によって異なります。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ空間 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ空間 | 任意の異なる2点 x,y\in X に対して, x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F に対して, F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| T_4 | 任意の2つの互いに素な閉集合 F,G\subset X に対して, F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| 正規 (normal) | T_1 かつ T_4( \iff T_2 かつ T_4\iff T_3 かつ T_4) |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの集合 A,B\subset X に対して, A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
| completely 正規 | T_1 かつ T_5( \iff T_2 かつ T_5\iff T_3 かつ T_5) |
チコノフの板は, T_4 だが T_5 でない空間の例としてよく挙げられます。あるいは,正規だが completely 正規ではないということもあります。
証明
T_0, T_1, T_2, T_3 であること
[0,\omega],[0,\omega_1] は T_0,T_1,T_2,T_3,T_4,T_5 全ての分離公理が成立するが,そのうち T_0,T_1,T_2,T_3 は,元の空間がそうなら直積空間もそうなるため,言える。
T_4 について
チコノフの板 T はコンパクトハウスドルフ空間であり,コンパクトハウスドルフ空間は T_4(正規)であるから, T は T_4 である。
欠けたチコノフの板 T_\infty が T_4 でないことを示そう。
F = \{\omega_1\}\times [0,\omega),\, G = [0,\omega_1)\times \{\omega\} とする。補集合が開集合なので, F, G は閉集合である。これが開集合で分離できないことを示そう。もし分離できるとすると,
F\subset U, \, G\subset V ,\, U\cap V=\emptyset
となる開集合 U, V\subset T_\infty が取れる。
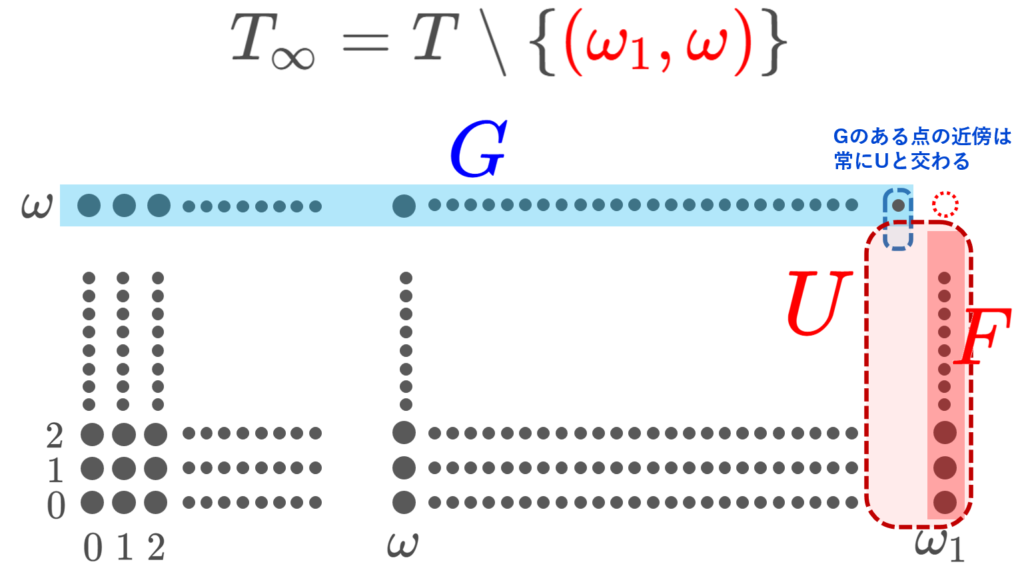
任意の点 (\omega_1, n)\in F に対し,ある \gamma_n \in [0,\omega_1) で, [\gamma_n, \omega_1]\times \{n\}\subset U となる開近傍 [\gamma_n, \omega_1]\times \{n\} が取れる。各 n ごとにこの \gamma_n を選ぶ。
\overline{\gamma}=\sup_n \gamma_n と定めると, \overline{\gamma}<\omega_1 である(→順序数に関する基本的なこと)。このとき,
[\overline{\gamma},\omega_1]\times [0,\omega)\subset U
である。 このとき, \{\overline{\gamma}+1\}\times [0,\omega)\subset U であるが, (\overline{\gamma}+1, \omega)\in G の近傍はこれと必ず交わるので, U\cap V\ne \emptyset である。
ゆえに, F,G は開集合で分離できず, T_\infty は T_4 空間でない。
T_5 について
T_5 空間であるとは,任意の部分空間が T_4 空間であることと同値である。 T_\infty は T_4 空間でないので, T は T_5 空間でない。
証明終
チコノフの板とコンパクト性
コンパクトにまつわる定義の確認をしておきましょう。
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 極限点コンパクト (limit point compact) | 任意の無限部分集合が集積点をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
コンパクトならば他の3つも成り立つので, T はコンパクトであることを示せばよいです。
証明
T について
[0,\omega_1],[0,\omega] はどちらもコンパクトであり,コンパクト空間の直積はコンパクトなので, T はコンパクトである。よって,極限点コンパクト・擬コンパクト・局所コンパクトでもある。
T_\infty について
\{\omega_1\}\times [0,\omega)\subset T_\infty は集積点をもたない無限集合であるから, T_\infty は極限点コンパクトではない。よって,コンパクトではない。
T_\infty が擬コンパクトであることを示そう。 f\colon T_\infty \to \R が連続であるとすると,f を制限した f(\cdot, \omega)\colon [0,\omega_1)\to \R も連続なので eventually constant,すなわちある \alpha_\omega \in [0,\omega_1) と x_\omega \in \R が存在して, f(\alpha, \omega)=x_\omega \; (\forall \alpha>\alpha_\omega) とできる(→順序位相の定義と順序数における順序位相の性質)。
ここで,f(\omega_1, \omega)=x_\omega として f を f\colon T\to \R に拡張すると,これも連続であり,T はコンパクトなので f は有界である。ゆえに,もとの連続関数 f\colon T_\infty\to\R も有界であり, T_\infty は擬コンパクトである。
また, (\alpha, \beta)\in T_\infty に対し, [0,\alpha]\times [0,\beta] はコンパクトな近傍なので, T_\infty は局所コンパクトである。
証明終
チコノフの板と連結性
| T | T_\infty | |
|---|---|---|
| 完全不連結 | 〇 | 〇 |
これは明らかでしょう。