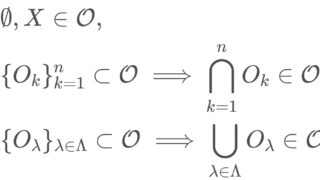ユークリッド空間・距離空間・位相空間における集積点・孤立点の定義と具体例を図解付きで解説します。特に,ユークリッド空間・距離空間における集積点・孤立点をしっかり理解していきましょう。
ユークリッド空間・距離空間における集積点・孤立点
まずは,ユークリッド空間や距離空間における集積点・孤立点について考えましょう。
ユークリッド空間・距離空間における集積点・孤立点の定義
ユークリッド空間で定義しますが,距離空間でも全く同じです。
定義1(数列を用いた集積点・孤立点の定義)
A\subset \R^d とする。
- x\in \R^d が A の集積点 (accumulation point, limit point) であるとは,ある数列 \{a_n\}_n\subset A\setminus\{x\} が存在して,
\large x=\lim_{n\to\infty}a_n
とできることをいう。また,集積点全体の集合を導集合 (derived set) という。 - x\in \R^d が A の集積点でなく,かつ x\in A であるとき,孤立点 (isolated point) であるという。
x 以外の A の点から,限りなく x に近づける場合は x は集積点であり,逆に近づけない場合,( x\in A なら)孤立点というわけです。
注意ですが, x が A に入るか否かは集積点の定義とは無関係です。一方で,孤立点は x\in A でなくてはなりません。
「限りなく近づける」という概念は,収束列ではなく,近傍を使って書き直すことができます。近傍を使って,集積点・孤立点の別の定義を述べておきましょう。
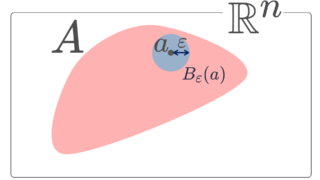
以下で, d(x,y)=\sqrt{\sum_{j=1}^d |x_j-y_j|^2} は2点 x,y\in \R^d の距離とし, \varepsilon >0 に対し,
B_\varepsilon (x)=\{ y\in \R^d\mid d(x,y)<\varepsilon \}
を x\in \R^d の \varepsilon-近傍とします。以下ではユークリッド空間 \R^d で定義しますが,ユークリッド空間に限らず,距離空間 (X, d) でも同じです。
定義2(近傍を用いた集積点・孤立点の定義)
A\subset \R^d とする。
- x\in \R^d が A の集積点 (accumulation point, limit point) であるとは,任意の \varepsilon>0 に対して,
\large B_\varepsilon(x)\cap (A\setminus\{x\}) \ne \emptyset
とできることをいう。 - x\in A が A の集積点でないとき,すなわち,ある \varepsilon>0 が存在して,
\large B_\varepsilon(x)\cap (A\setminus\{x\}) = \emptyset
が成り立つとき, x を A の孤立点 (isolated point) であるという。
x のまわりの任意に小さな近傍と A が, x 以外に共有点をもつならば,x は集積点であり,逆に x のまわりのとある近傍の中に,x 以外に A の元が入らないようにできるなら孤立点です。
ユークリッド空間における集積点・孤立点の具体例
具体例を見ていきましょう。
例1.
\R において, A=(0,1]\cup \{2\} とする。このとき, A の集積点全体の集合(導集合)は [0,1] であり, A の孤立点は 2 のみである。
[0,1] の各点には,その点以外の A の点から,その点に収束する数列が取れますが, 2 に収束する A\setminus\{2\}=(0,1] に入る数列は取れないので, 2 は孤立点です。
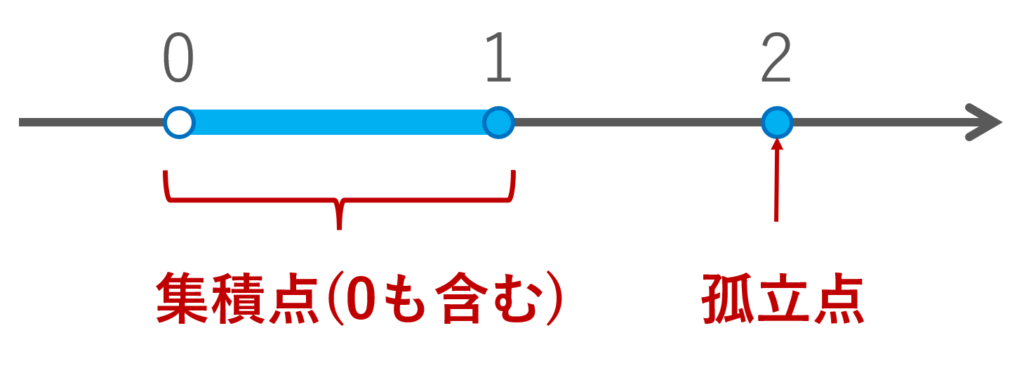
言葉の通り, 2 は孤立していますね。
例2.
\R^2 において, A=\{(x,y)\in \R^2\mid \{0<x^2+y^2<1\} とする。このとき, (0,0) は A の集積点であり,\R^2 \setminus A の孤立点である。
以下の図では,集合 A を赤でかいてみました。真ん中の点は,赤の集合から限りなく近づけるので,赤の集合における集積点ですが,白の集合(赤の外の周りを含む)から見ると,孤立しているので孤立点です。

次はものすごくいい例だと思います。
例3.
A\subset \R を A=\{ 1/n \mid n\ge 1\} とする。
このとき, A のすべての点は孤立点であり, A の集積点は 0 のみである。
0 は A には属していませんが, A の唯一の集積点です。
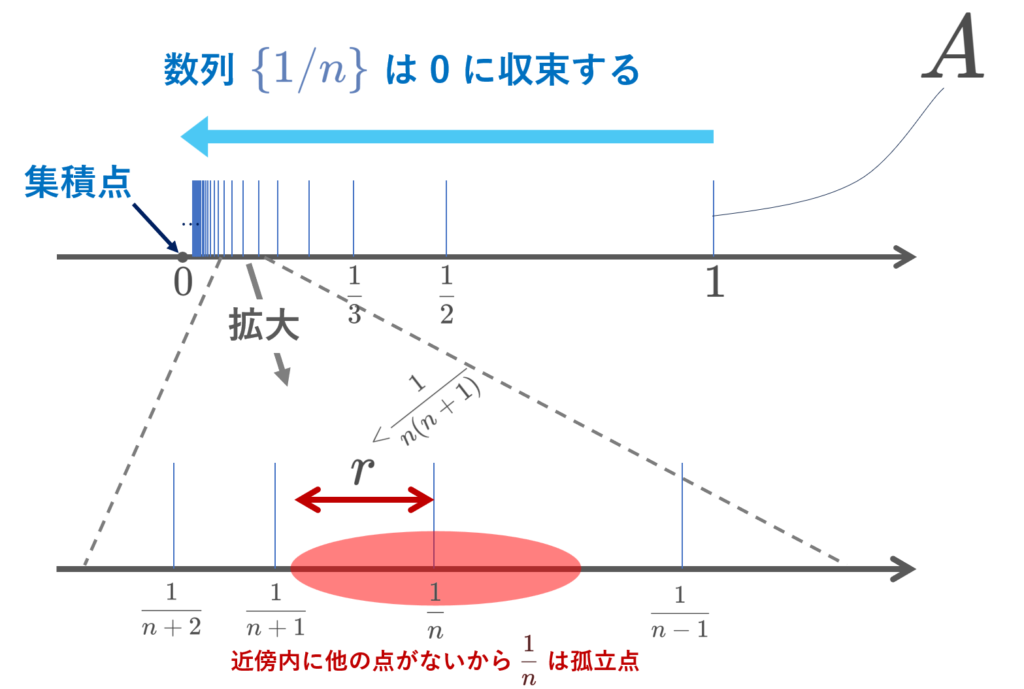
0 が集積点である理由は, A 内から 0 に収束する数列を, \{1/n\}\subset A と取ることができるからです。
一方で, 1/n\in A は孤立点です。 1/n 以外の A の点から, 1/n に収束することはできません。また, r< \frac{1}{n(n+1)} とすると, (\frac{1}{n}-r, \frac{1}{n}+r)\cap (A\setminus\{1/n\})=\emptyset となることからも,孤立点であることが確認できます。
位相空間における集積点・孤立点
さて,より一般の位相空間における集積点・孤立点を定義しましょう。
ユークリッド空間・距離空間のイメージがしっかりしていて,その一般化が位相空間であることが分かっていれば,以下の定義はそんなに不自然なものでないでしょう。
定義3(位相空間における集積点・孤立点の定義)
(X,\mathcal{O}) を位相空間とし, A\subset X とする。
- x\in X が A の集積点 (accumulation point) であるとは,
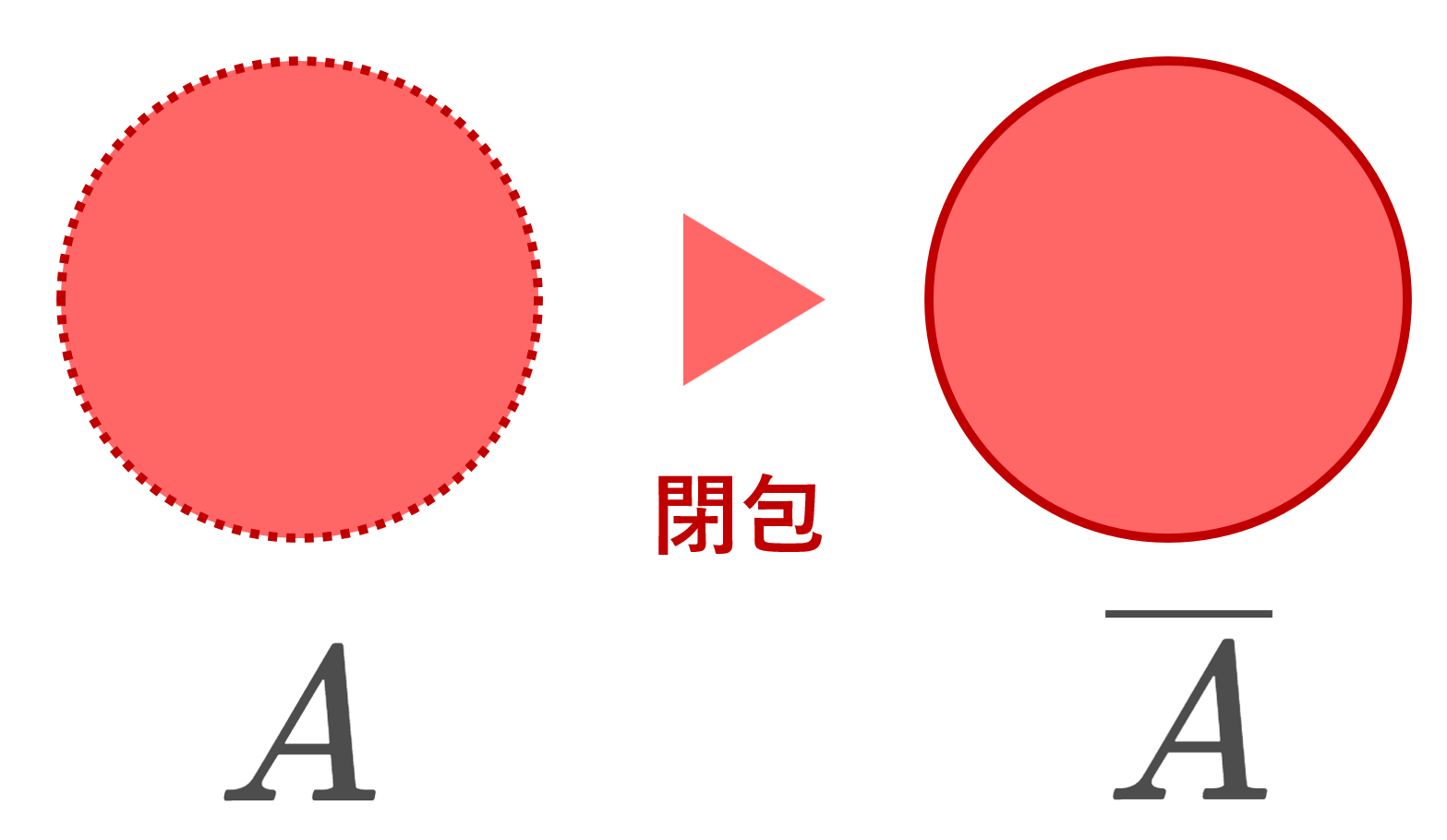
\large x\in \overline{A\setminus\{x\}}
が成り立つことを言う。 - x\in X が A の孤立点 (isolated point) であるとは, x\in A かつ
\large x\not\in \overline{A\setminus\{x\}}
が成り立つことを言う。
よくわからない場合は,まず以下のような記事を追ってみるとよいでしょう。
例4(離散位相・密着位相).
(X, 2^X) を離散位相とし, A\subset X は空でないとする。このとき, A に属する全ての点は A の孤立点である。
(X, \{ \emptyset, X\}) を密着位相とし, A\subset X は空でないとする。このとき, X\setminus A の各点は A の集積点である。また, A が2点以上の集合のときは A の各点も集積点である。 A が1点集合のときは A の各点は孤立点である。
離散位相のときは, \overline{A\setminus\{x\}}=A\setminus \{x\} です。
密着位相のときは, \overline{A\setminus\{x\}} =\begin{cases} \emptyset & A=\{x\}, \\ X & A\setminus\{x\}\ne \emptyset\end{cases} です。
個人的には,集積点・孤立点という用語は,一般の位相空間で使うことはあまりなく,ユークリッド空間や距離空間で使うことの方が多い気がします。あくまで個人的な話です。