箱ひげ図とは,データの最小値・第一四分位数・中央値・第三四分位数・最大値を可視化するツールです。箱ひげ図について,定義を図解して紹介しましょう。
箱ひげ図とは
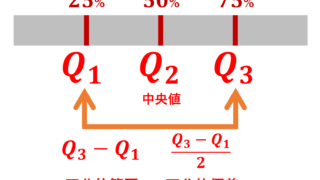
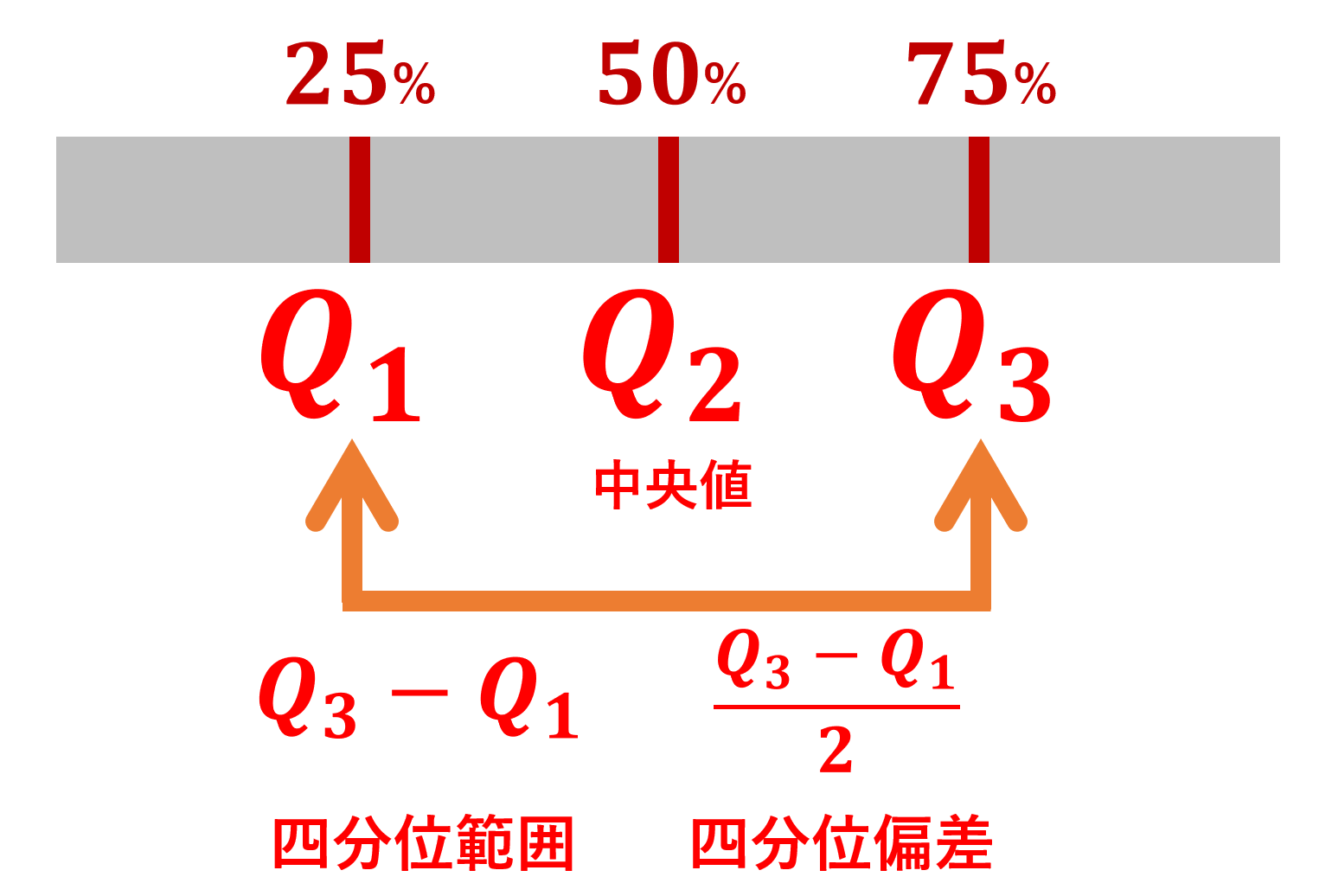
データの最小値・第一四分位数・中央値・第三四分位数・最大値を用いてデータのばらつきを表すことを五数要約 (five-number summery) といいます。特に第一四分位数 Q_1,中央値 Q_2,第三四分位数 Q_3 は,データを昇順に並べたときに,小さい順からそれぞれ 25\%, 50\%, 75\% の値を表します。このときの Q_3-Q_1 を四分位範囲 (interquartile range; IQR)といいます。
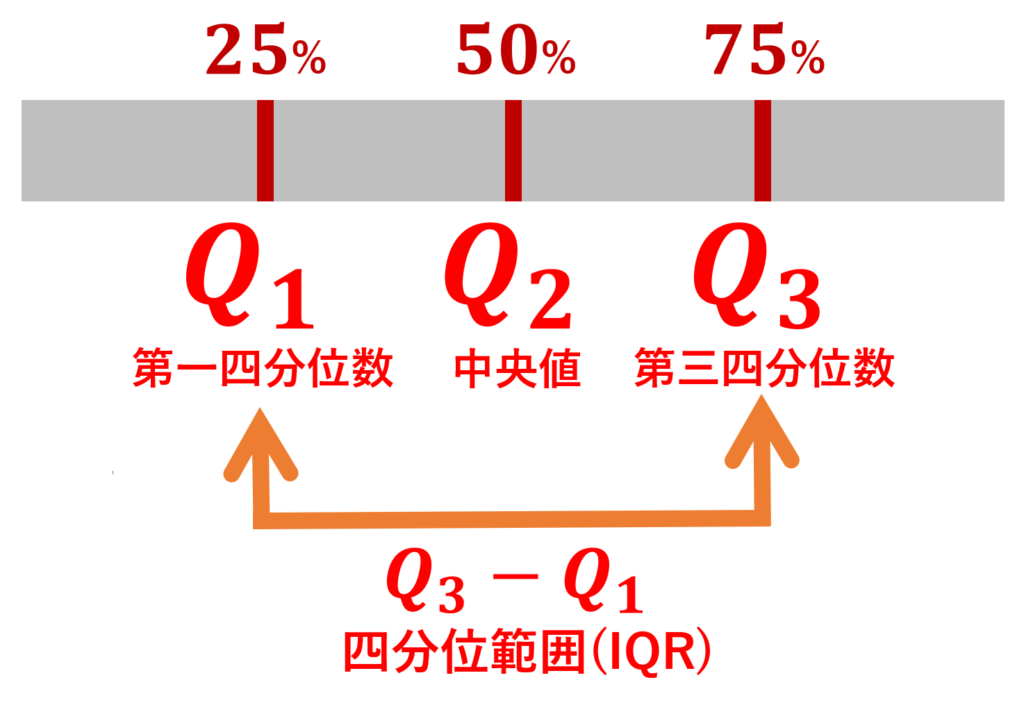
Q_1, Q_3 の決め方など詳しくは四分位数・四分位範囲・四分位偏差をわかりやすく図解で解説しています。
これを可視化したのが箱ひげ図です。
定義(箱ひげ図)
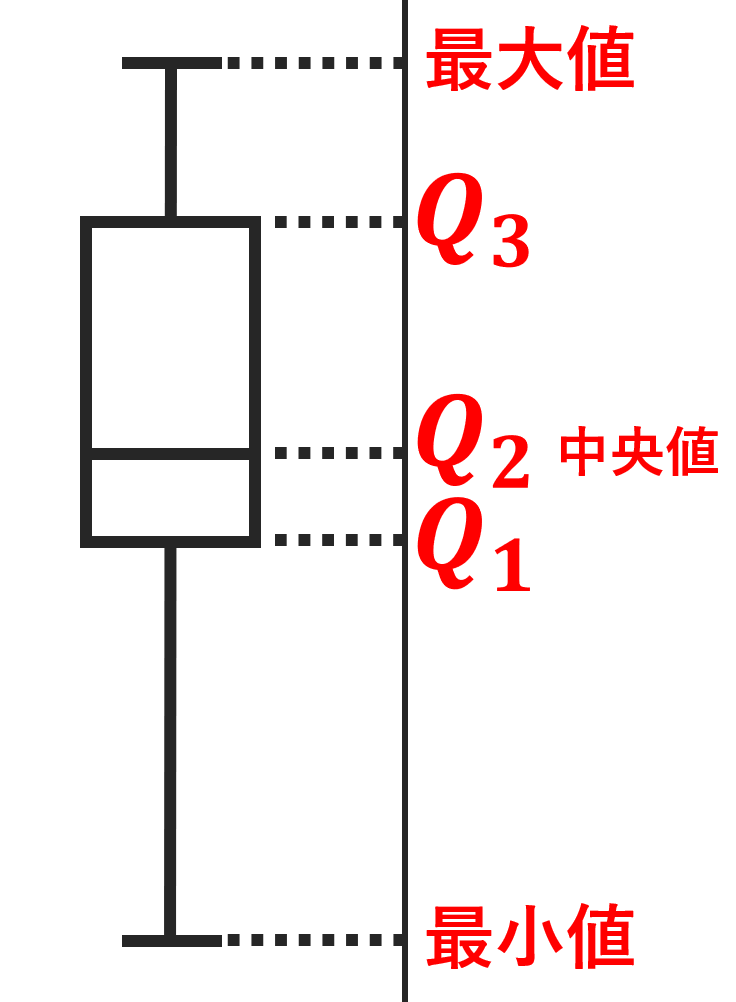
データにおいて,最小値・第一四分位数・中央値・第三四分位数・最大値の5つの数値を可視化した以下のような図を箱ひげ図 (box plot) という。
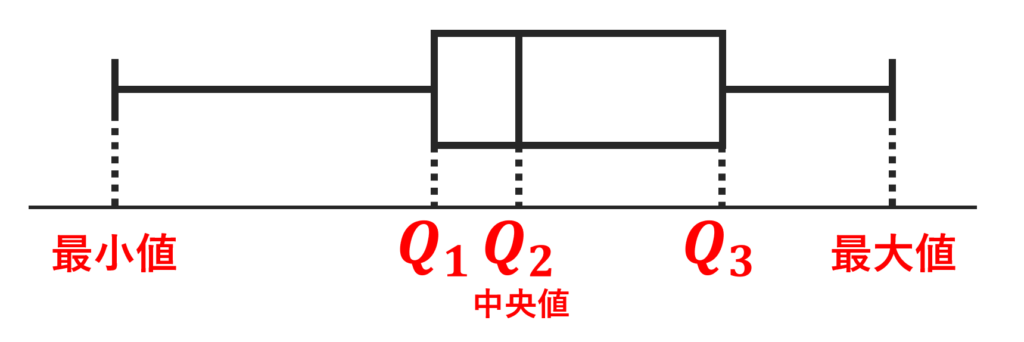
箱ひげ図はデータの分布の様子をみるツールの一つですね。箱ひげ図の四角の部分を箱,線の部分をひげといいます。
なお,箱ひげ図には以下のように平均値を含めることもあります。
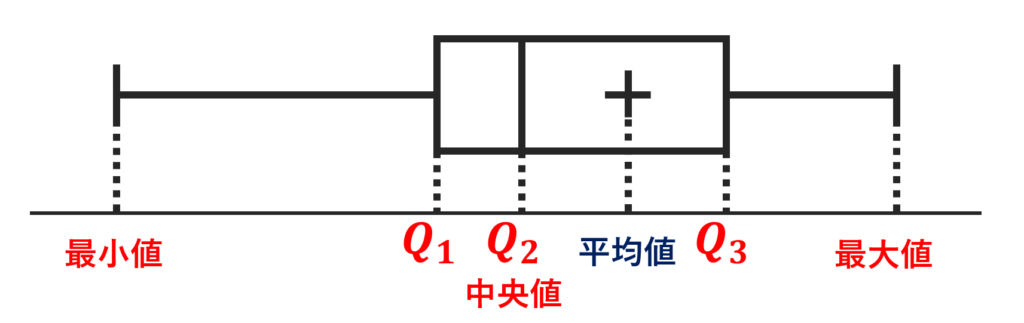
また,箱ひげ図は縦にかくことも多いです。
外れ値を考慮した箱ひげ図
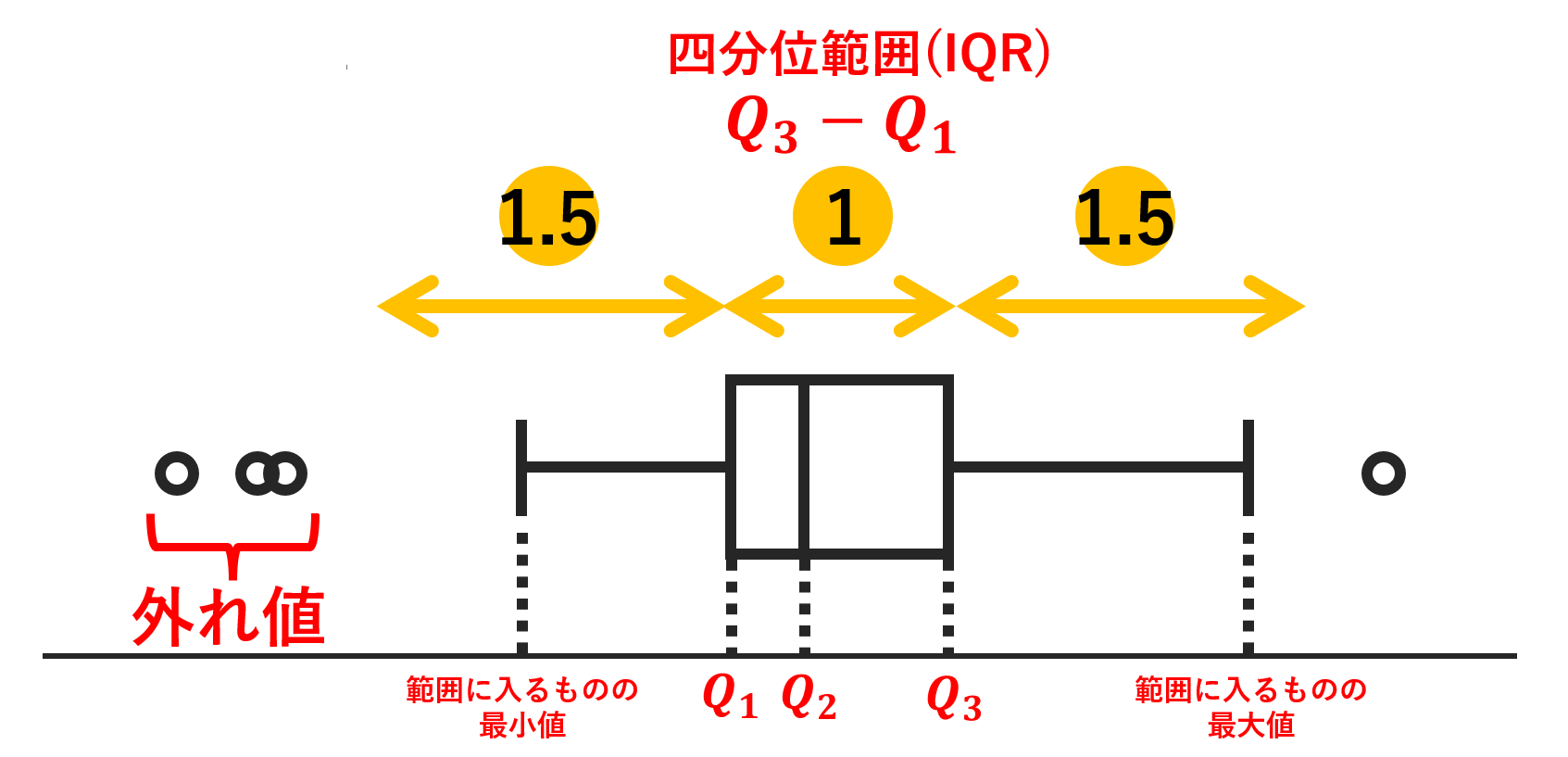
箱ひげ図における「ひげ」の長さは,最小値・最大値の値に大きく左右されます。ヒューマンエラーや測定機器のエラーにより,最小値・最大値の値が大きく「外れ」てしまったら困りますよね。そこで,外れ値を考慮した箱ひげ図をかくことがあります。
特によく使われるのは,四分位範囲を \text{IQR}=Q_3-Q_1 としたときに,区間
[Q_1-1.5\text{(IQR)}, Q_3+1.5\text{(IQR)}]
に入らないものを外れ値 (outlier) とする手法です。以下の図を見てください。
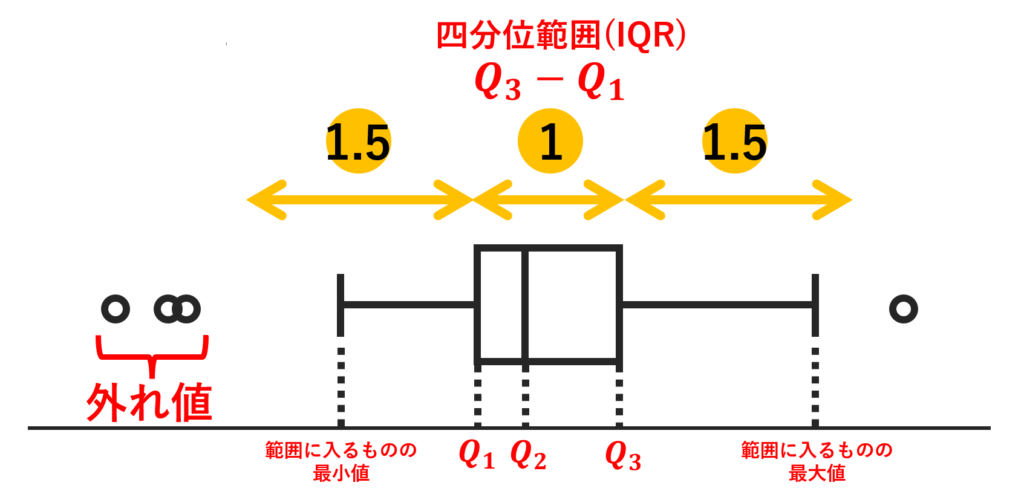
このようにすることで,外れた値に左右されない箱ひげ図が描けますね。
ヒストグラムと箱ひげ図
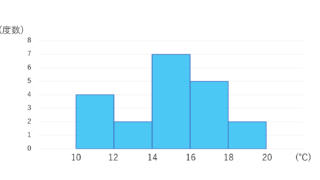
データの部分を可視化する別の手段としてヒストグラム (histogram) は有名でしょう。ヒストグラムと箱ひげ図の大まかな対応を確認しておきましょう。
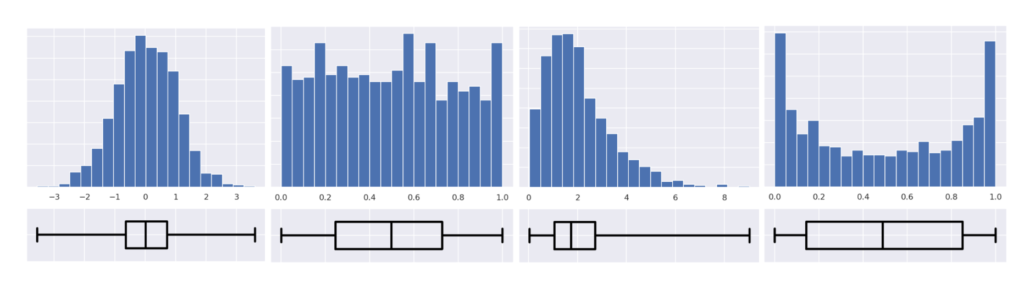
ヒストグラムと箱ひげ図は概ね対応しているのが分かるでしょう。