ほうき空間とは,ざっくり言うと平面上において,ある点から放射状に無限本の線分を伸ばした位相空間です。見た目からほうき空間と呼ばれることがあります。ほうき空間自体も面白いですが,後で紹介するほうき空間の無限個の繋ぎ合わせが面白いです。見ていきましょう。
ほうき空間(Broom Space)
定義(ほうき空間)
\R^2 において,原点と点 (1,1/n) を結んだ線分(端点含む)を I_{1/n} とかき,
\large \color{red} B=\left(\bigcup_{n=1}^\infty I_{1/n}\right) \cup \Bigl( (1/2,1]\times \{0\}\Bigr)
を考える。位相空間 B\subset \R^2 をほうき空間 (infinite broom, broom space) という。
また,その閉包 \color{red} \overline{B}=B\cup ([0,1/2]\times \{0\}) を閉ほうき空間 (closed infinite broom, closed broom space) という。
ちょっとわかりにくいですが,B,\overline{B} を色分けしてかくと下の図のようになります。
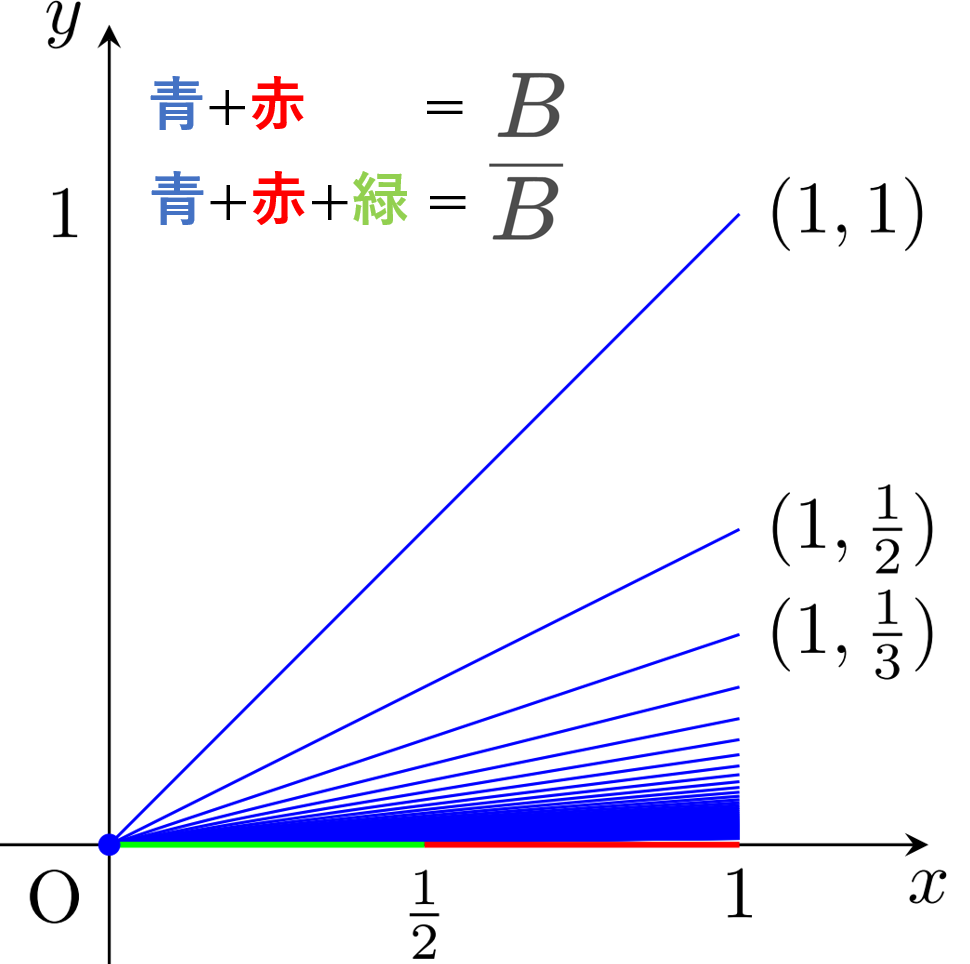
ほうき空間の位相的性質
| B | \overline{B} | |
|---|---|---|
| 第一可算・第二可算・可分 | 〇 | 〇 |
| 距離化可能 | 〇 | 〇 |
| T_0, T_1,T_2, T_3, T_4, T_5 空間 | 〇 | 〇 |
| コンパクト・点列コンパクト | × | 〇 |
| 局所コンパクト | 〇 | 〇 |
| 連結 | 〇 | 〇 |
| 弧状連結・弧連結 | × | 〇 |
| 局所連結 | × | × |
一つずつみていきましょう。
1. 第一可算・第二可算・可分であること
第二可算の部分空間は第二可算だし,第二可算なら第一可算なので,第一可算・第二可算は明らかです。
また, B や \overline{B} における有理点全体は稠密な可算集合なので可分です。
可分であることは,第二可算であることと,距離空間において可分性と第二可算性は同値であることからも従います。
2. 距離化可能であること・T0からT5空間までの全てをみたすこと
\R^2 の部分空間からのユークリッド距離によって, B,\overline{B} は距離化可能です。
距離空間は, T_0 から T_5 まで全てみたすので,示せました。
3. コンパクト性について
コンパクト性について本サイトでは,以下の定義を採用しています。
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
\overline{B} は \R^2 における有界閉集合ですから,コンパクトです。よって局所コンパクトでもあり,さらに距離空間においては,コンパクト性と点列コンパクト性は同値なので,点列コンパクトでもあります。
一方で,明らかに B は閉集合ではないため,コンパクト・点列コンパクトではありません。
しかし,任意の x\in B に対し, x の \R^2 における閉近傍を十分小さくとれば, B との共通部分が \R^2 における有界閉集合にできるため, B は局所コンパクトではあります。
4. 連結性について
連結にまつわる定義は以下の通りです。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な空でない開集合 U,V で, U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について,ある連続写像 f\colon [0,1]\to X で, f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として,埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる(※単に全単射なものが取れるとすることもある。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値) |
| 局所連結 (locally connected) | 各点で連結な基本近傍系をもつ |
J=\bigcup_{n=1}^\infty I_{1/n} は明らかに弧連結であり,弧連結 \implies 弧状連結 \implies 連結ですから,J は連結です。また, J\subset B\subset \overline{J}=\overline{B} であるので, B,\overline{B} も連結です。
一方で,2点 (0,0), (1,0)\in B を結ぶ B 上の道はないので, B は弧状連結ではありません。
また, B,\overline{B} はどちらも (3/4, 0) まわりで連結な基本近傍系をもたないので,局所連結ではありません。
無限個繋ぎ合わせたほうき空間
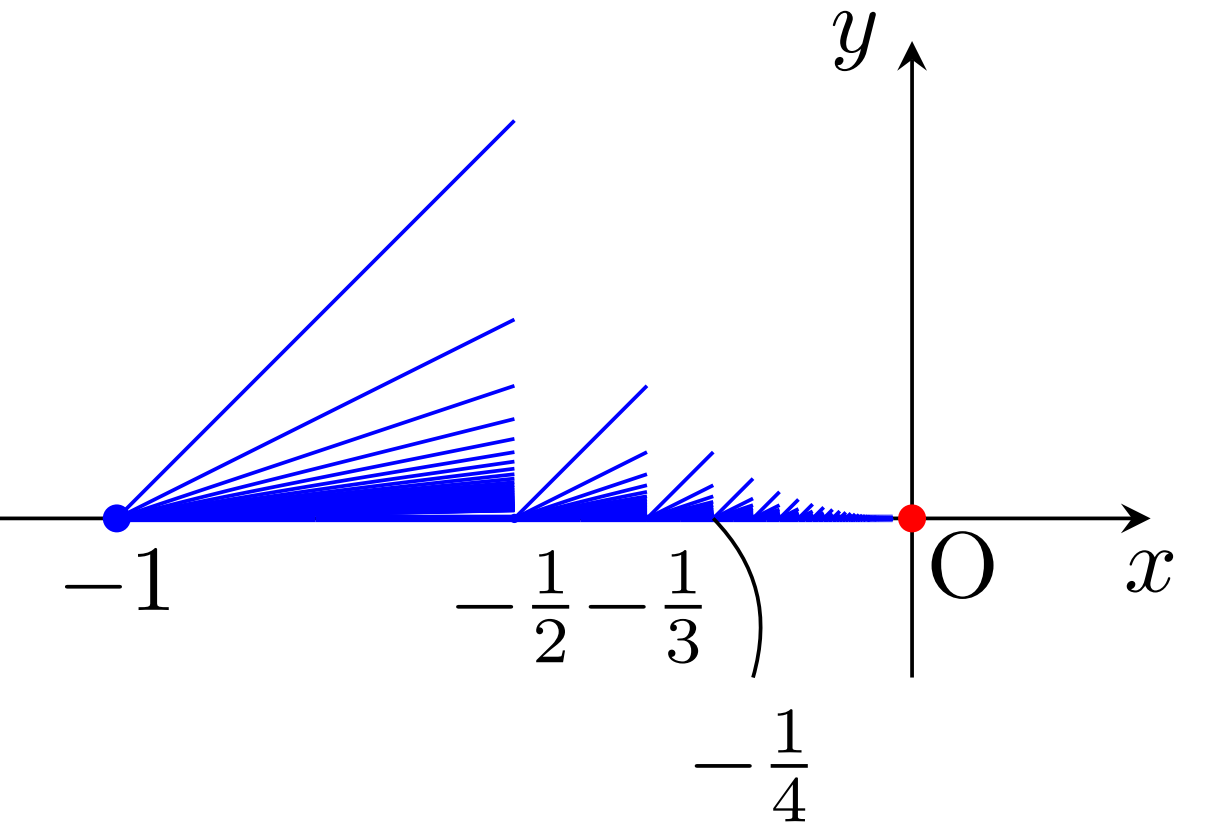
閉ほうき空間 \overline{B} を図のように縮小・平行移動して無限個貼り合わせ,さらに原点を合わせた位相空間 \large\color{red}\overline{ B_\infty} を考えます。
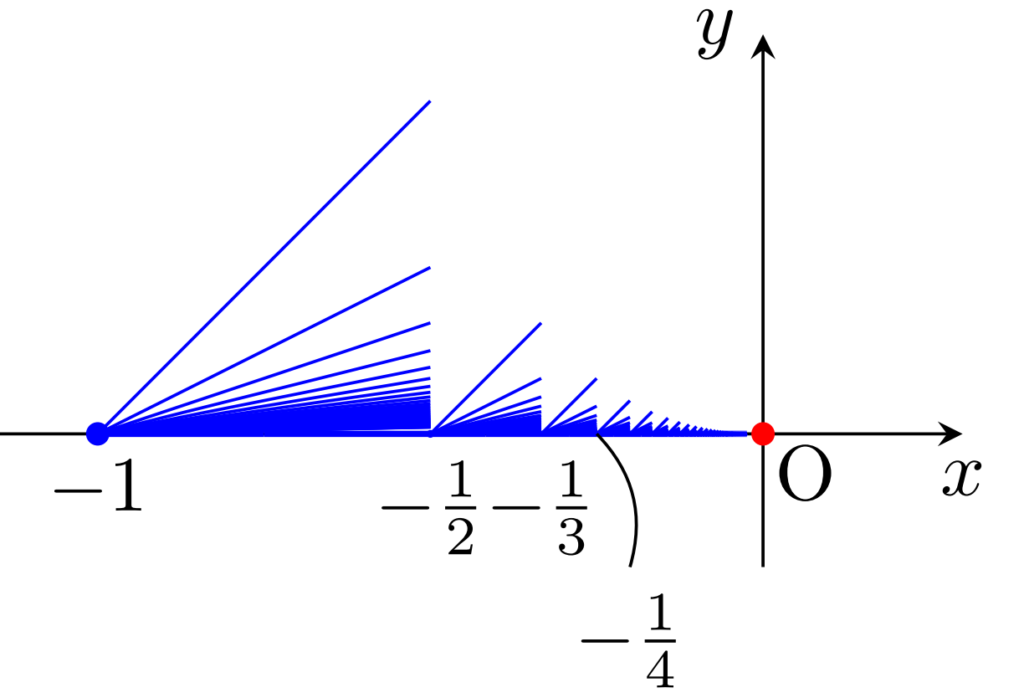
\overline{B_\infty} は \R^2 の閉部分空間であり,コンパクト・連結・弧状連結ですが,局所連結ではありません。局所連結でないのは, \overline{B} がそうでなかったのと同じです。
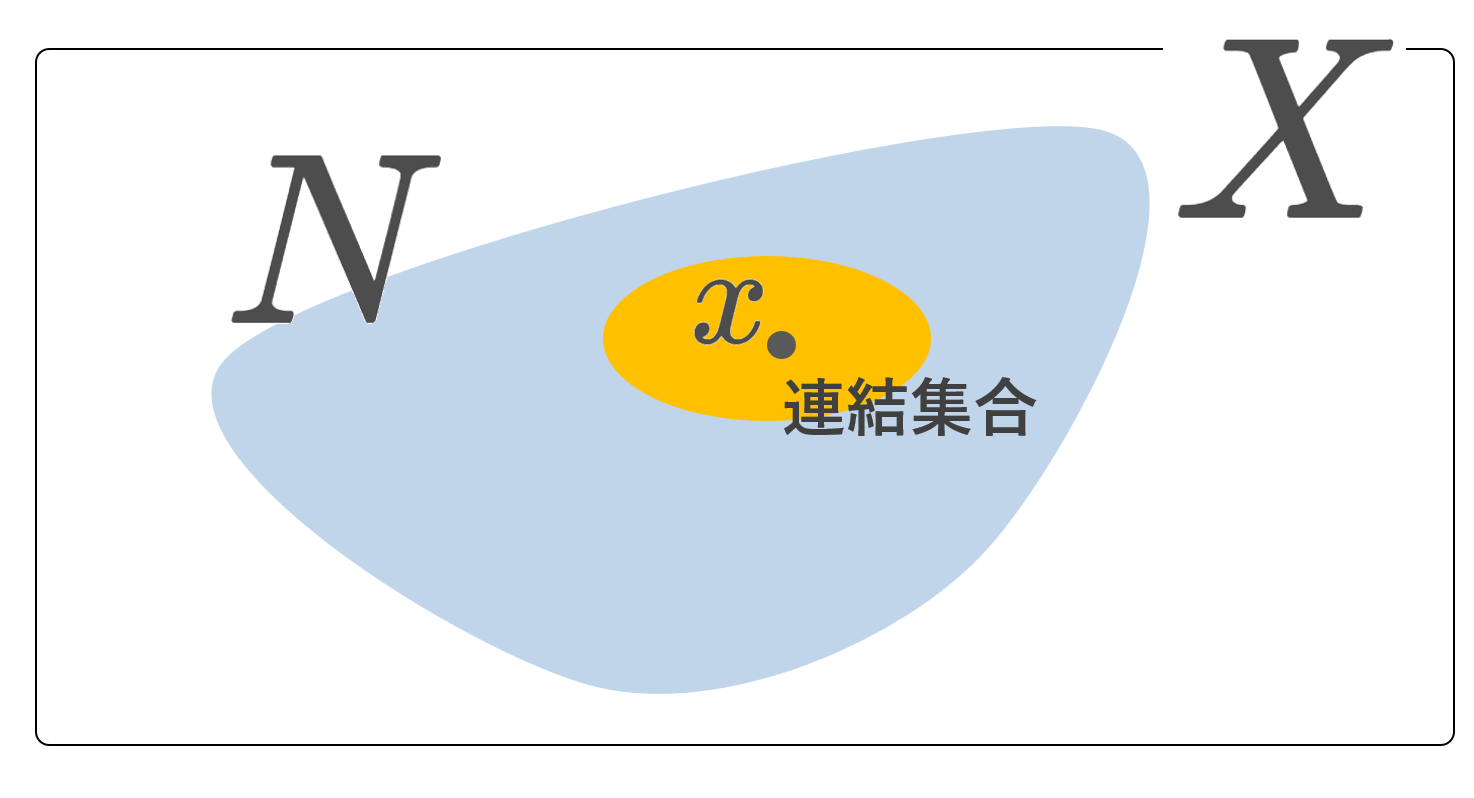
ここで,\overline{B_\infty} には面白い性質があります。それは,原点において弱局所連結ですが,原点において局所連結でないという性質です。まずは2つの定義を確認しておきましょう。
これは各点ごとの定義であり,空間全体としての局所連結とはまた話が違うことに注意してください。この辺の定義については,局所連結とは~定義・具体例・性質~で解説しています。
今の場合,原点の開近傍で連結なものは存在しないため,原点において局所連結ではありません。一方で, n\ge 1 に対し,
\overline{B_\infty}\cap \{(x,y)\in\R^2 \mid x\ge -1/n\}
は原点における基本近傍系になっているので,原点において弱局所連結です。
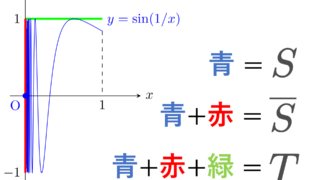
ほうき空間そのものは,くし空間 (comb space) や位相幾何学者の正弦曲線 (topologist’s sine curve) とほぼ同じ性質なので,あまり取り上げられる機会は少ないかもしれません。ただ,無限個繋ぎ合わせたほうき空間の例は上記の点で重要です。