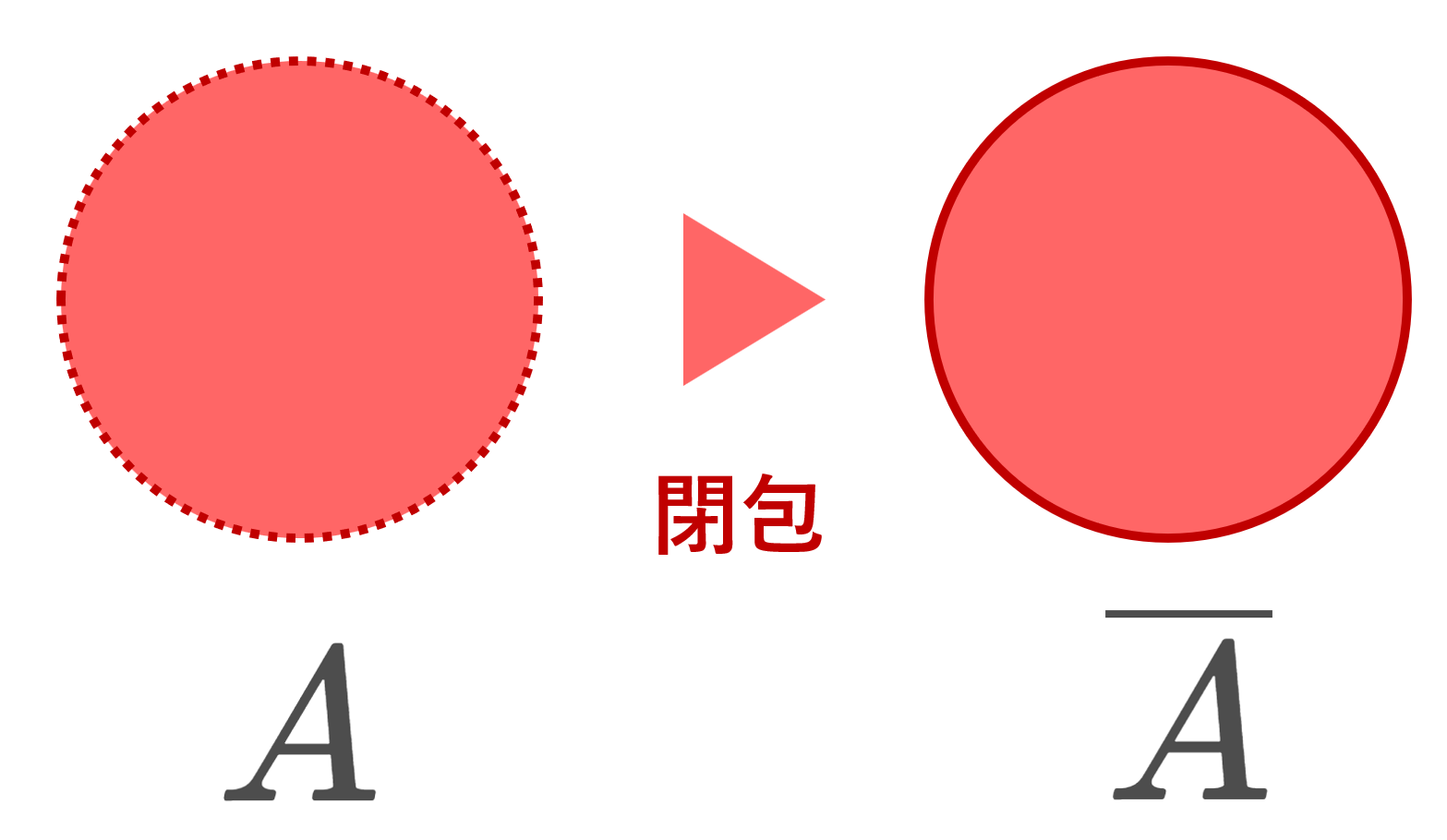
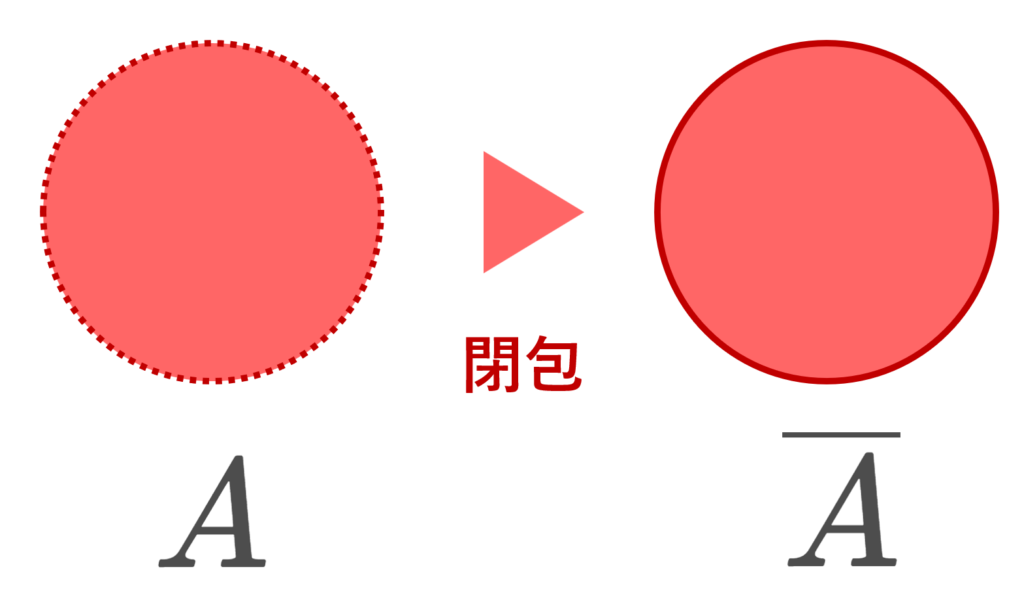
ユークリッド空間・距離空間・位相空間におけるある集合の「閉包」とは，ある集合を含む最小の閉集合のことです。まずは位相空間における一般的な閉包を定義し，ユークリッド空間・距離空間におけるもっとイメージしやすい定義を述べましょう。
閉包の定義
まずは一般の位相空間における閉包を定義し，より具体的なユークリッド空間・距離空間における別の定義を紹介しましょう。
位相空間における閉包の定義
まずは，一般の位相空間における閉包の定義を述べます。
定義1（閉包）
(X,\mathcal{O}) を位相空間とし， A\subset X とする。
A を含む最小の閉集合を A の閉包 (closure) といい， A^a や \color{red}\large \overline{A} や \operatorname{Cl}(A) などとあらわす。
定義から明らかに A\subset \overline{A} です。
高校では，\overline{A} は A の補集合を表していたと思いますが，大学では A^c で A の補集合を表し， \overline{A} で A の閉包を表すのが普通です。
\mathcal{C}_A を A を含む閉集合全体としたとき， \bigcap_{C\in\mathcal{C}_A} C も A を含む閉集合ですから，「 A を含む最小の閉集合」を考えることができます。
開集合の補集合が閉集合，閉集合の補集合が開集合ですから， X\setminus \overline{A} は， X\setminus A に含まれる最大の開集合(すなわち集合 X\setminus {A} の内部(開核))です。
ユークリッド空間・距離空間における点列を用いた定義
さて，より具体的なユークリッド空間・距離空間では，閉包は別な定義が可能ですから，それを紹介しましょう。何でもかんでも一般的な定義だけ分かっているだけではダメで，イメージを持ちやすい定義を理解しておくのが大切です。
以下では，距離空間で定義しますが，ユークリッド空間 \R^n としてもよいです。
定義2（点列の収束と閉集合）
(X, d) を距離空間とし， A\subset X とする。
A における収束する数列 \{a_n\}\subset A の収束先となり得る点全体の集合を A の閉包 (closure) といい， A^a や \color{red}\large \overline{A} や \operatorname{Cl}(A) などとあらわす。
たとえば， a\in A に対し， a,a,a,\ldots という定数列は a に収束しますから， A\subset \overline{A} が成り立ちます。
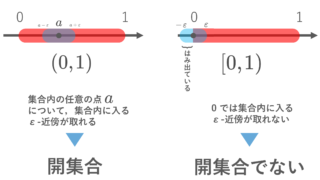
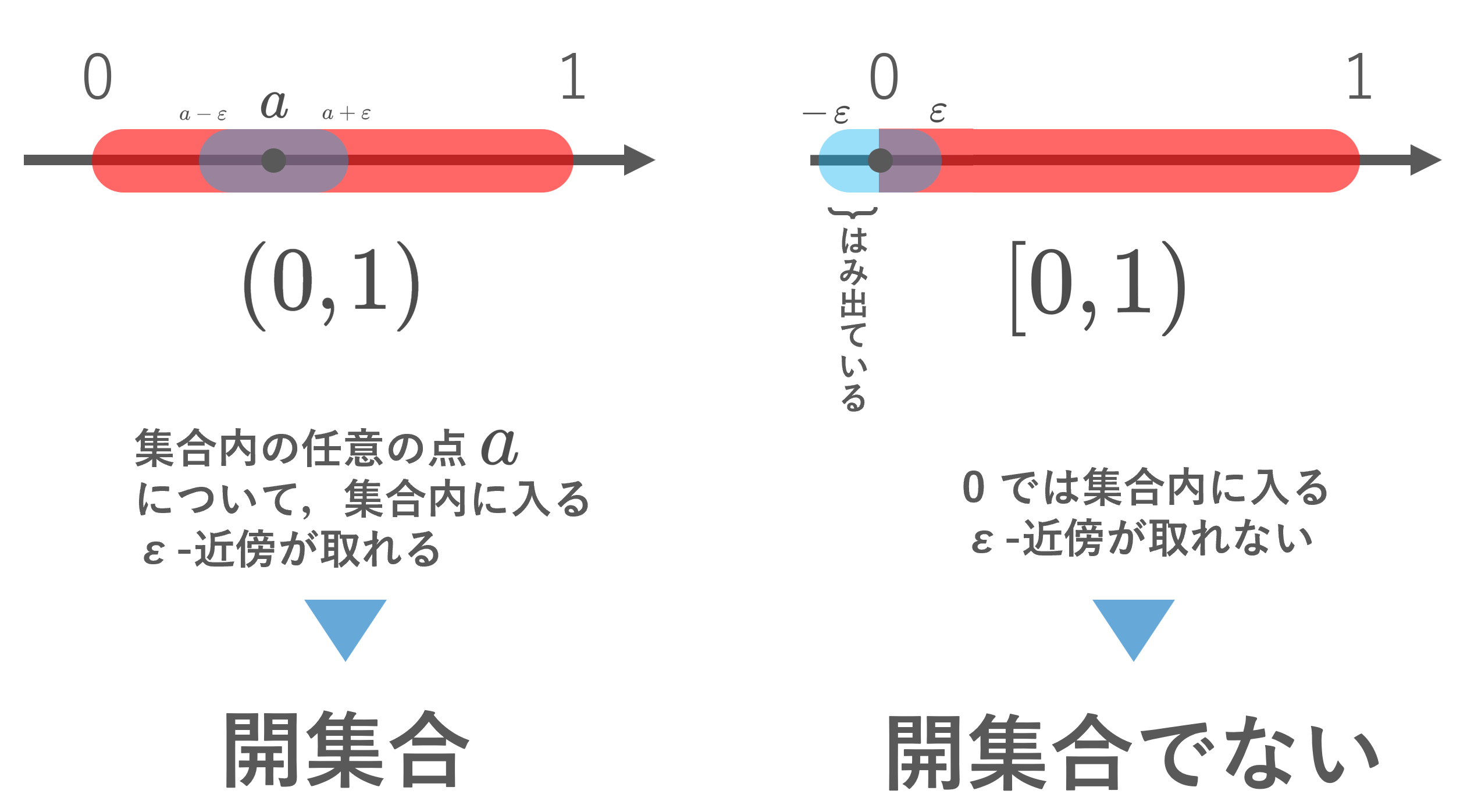
分かりやすい定義だと思います。たとえば，収束する数列 \{a_n\}\subset (0,1) の収束先としてあり得る範囲は [0,1] なので， \overline{(0,1)}=[0,1] です。
【距離空間】内部(開核)・境界の概念を用いた定義～触点全体の集合～
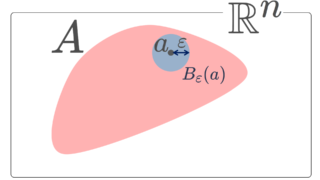
(X, d) を距離空間とします。 \varepsilon >0 に対し，点 a\in X における \varepsilon-近傍を
\textcolor{red}{\large B_\varepsilon(a)}=\{ x\in X \mid d(a, x)<\varepsilon\}
とかくことにします。
定義3（触点・閉集合）
(X, d) を距離空間とし， A\subset X とする。
x\in X が，任意の \varepsilon>0 に対して，
\Large \color{red} B_\varepsilon (x)\cap A \ne \emptyset
をみたすとき，x は A の触点 (adherent point, point of closure) という。触点全体の集合を A の閉包 (closure) といい， A^a や \color{red}\large \overline{A} や \operatorname{Cl}(A) などとあらわす。
定義より明らかに A\subset \overline{A} です。
触点とは，集合の内点か境界点です(→内部(開核)・外部・境界について詳しく図解～距離空間・位相空間～)。よって，集合の閉包とは，集合の内部と境界の和集合といえます。すなわち，
\large \overline{A} =\operatorname{Int}(A)\cup \partial A
です。詳しくは
も見てください。
閉包の具体例
例1( \R).
実数 \R の部分集合について，
- \overline{(0,1)}=\overline{[0,1)}=\overline{[0,1]}=[0,1]
- \overline{\{a\}}=\{a\}
- \overline{\mathbb{Q}}=\overline{\mathbb{R}\setminus\mathbb{Q}}=\mathbb{R}
例2( \R^2).
\R^2 の部分集合について
- \begin{aligned} &\overline{\{(x,y)\in\R^2\mid x^2+y^2<1\}} \\&=\{(x,y)\in\R^2\mid x^2+y^2\le 1\}\end{aligned}
- \begin{aligned} &\overline{\{(x,y)\in\R^2\mid x^2+y^2=1\}} \\&=\{(x,y)\in\R^2\mid x^2+y^2=1\}\end{aligned}
例3(離散距離).
(X, d) を離散距離空間とする。すなわち， d(x,y)=\begin{cases} 1 & x\ne y, \\ 0& x=y\end{cases} とする。このとき，任意の A\subset X に対し， \overline{A}=A である。
どの点同士の距離も 1 なので， \{a_n\}\subset A が収束するには，最終的に定数列 a,a,a,a,\ldots にならねばなりません。 a\in A ですから， A 内にしか収束できません。
例4(密着位相).
(X, \mathcal{O}) を密着位相空間とする。このとき，
\overline{A} = \begin{cases} \emptyset & A=\emptyset, \\ X & A\ne \emptyset\end{cases}
である。
密着位相空間における閉集合は \emptyset と X のみですから，明らかです。
なお，離散位相は例3.と同じです。
閉包の性質
定理（閉包の性質）
(X,\mathcal{O}) を位相空間とし， A,B\subset X とする。このとき，
- \overline{\emptyset}=\emptyset, \;\overline{X} = X
- A\subset \overline{A}
- \overline{\bigl(\overline{A}\bigr)}=\overline{A}
- \overline{A\cup B} = \overline{A}\cup \overline{B}
これを帰納的に用いると，
\overline{A_1\cup A_2\cup \cdots \cup A_n} = \overline{A_1}\cup \overline{A_2}\cup\cdots\cup \overline{A_n} - 4.はさらに一般的に， \{A_\lambda\}_{\lambda\in \Lambda} を局所有限 (locally finite) な部分集合としたとき， \overline{\bigcup_{\lambda\in\Lambda} A_\lambda}=\bigcup_{\lambda\in\Lambda} \overline{A_\lambda} が成り立つ。
\{A_\lambda\}_{\lambda\in \Lambda} が局所有限 (locally finite) であるとは，任意の x\in X に対し，ある x の開近傍 U が存在して， U\cap A_\lambda\ne\emptyset となる \lambda\in\Lambda が有限個(0個を含む)しかないようにできることをいいます。
なお，4.の \cup を \cap に置き換えたものは，一般に \overline{A\cap B} \subset \overline{A}\cap \overline{B} ですが，等号は成り立ちません。実際， A\cap B\subset \overline{A}, \overline{B} なので， A\cap B \subset \overline{A}\cap \overline{B} がいえます。右辺は閉集合なので， \overline{A\cap B} \subset \overline{A}\cap \overline{B} となります。一方で， \R において， A = [0,1),\; B =(1,2] とすると，
\begin{aligned}\overline{A\cap B}&=\overline{\emptyset}=\emptyset,\\ \overline{A}\cap \overline{B}&= [0,1]\cap [1,2]=\{1\} \end{aligned}
となって，異なる集合となります。
1.から3.は定義より明らかなので，4.と5.のみ証明しましょう。
4.と5.の証明
4.について
A\cup B\subset \overline{A}\cup \overline{B} であり，右辺は閉集合であるから，
\overline{A\cup B}\subset \overline{A}\cup \overline{B}
が成り立つ。一方で， A\cup B\supset A より， \overline{A\cup B}\supset \overline{A} であり，同様に \overline{A\cup B}\supset \overline{B} であるから，
も成り立つ。よって， \overline{A\cup B}= \overline{A}\cup \overline{B} である。
5.について
各 \lambda\in \Lambda について， \overline{ A_\lambda}\subset \overline{\bigcup_{\lambda\in\Lambda}A_\lambda} より， \bigcup_{\lambda\in\Lambda} \overline{A_\lambda}\subset\overline{\bigcup_{\lambda\in\Lambda} A_\lambda} はよい。
x\in \overline{\bigcup_{\lambda\in\Lambda}A_\lambda} とすると， x のある開近傍 U が存在して， U\cap A_{\lambda}\ne\emptyset となる \lambda\in \Lambda は有限個しかない。それを \lambda_1, \lambda_2,\ldots, \lambda_n とすると， (U \cap \bigcup_{\lambda\in\Lambda}A_\lambda) \subset \bigcup_{k=1}^n A_{\lambda_k} である。
x の任意の開近傍 V に対し， V\cap \left(\bigcup_{\lambda\in\Lambda}A_\lambda\right)\ne \emptyset であるから， x の任意の開近傍 V に対し，
V\cap \left(\bigcup_{k=1}^n A_{\lambda_k}\right)\ne \emptyset
とならねばならない(そうでないと U\cap V\cap \left(\bigcup_{\lambda\in\Lambda}A_\lambda\right)\subset V\cap \left(\bigcup_{k=1}^n A_{\lambda_k}\right) =\emptyset となってしまい， U\cap V も x の開近傍であることに矛盾する)。よって，4.より，
なので， x\in \bigcup_{\lambda\in\Lambda} \overline{A_\lambda} である。ゆえに， \overline{\bigcup_{\lambda\in\Lambda} A_\lambda}\subset\bigcup_{\lambda\in\Lambda} \overline{A_\lambda} もいえた。よって結論を得る。
証明終
なお，5.は局所有限でない無限個の集合では成り立ちません。たとえば， A_n = \{1/n\} とすると，
\begin{aligned}\overline{ \bigcup_{n=1}^\infty A_n} &= \{ 1/n \mid n \ge 1\} \cup \{0\}, \\ \bigcup_{n=1}^\infty \overline{A_n} &= \{ 1/n \mid n \ge 1\} \end{aligned}
となって，等号が成り立ちません。5.の証明中にも出てきたように，一般には \overline{\bigcup_{\lambda\in\Lambda} A_\lambda}\subset\bigcup_{\lambda\in\Lambda} \overline{A_\lambda} です。
