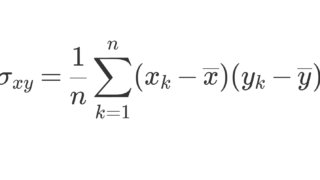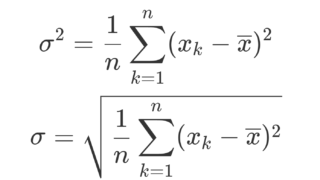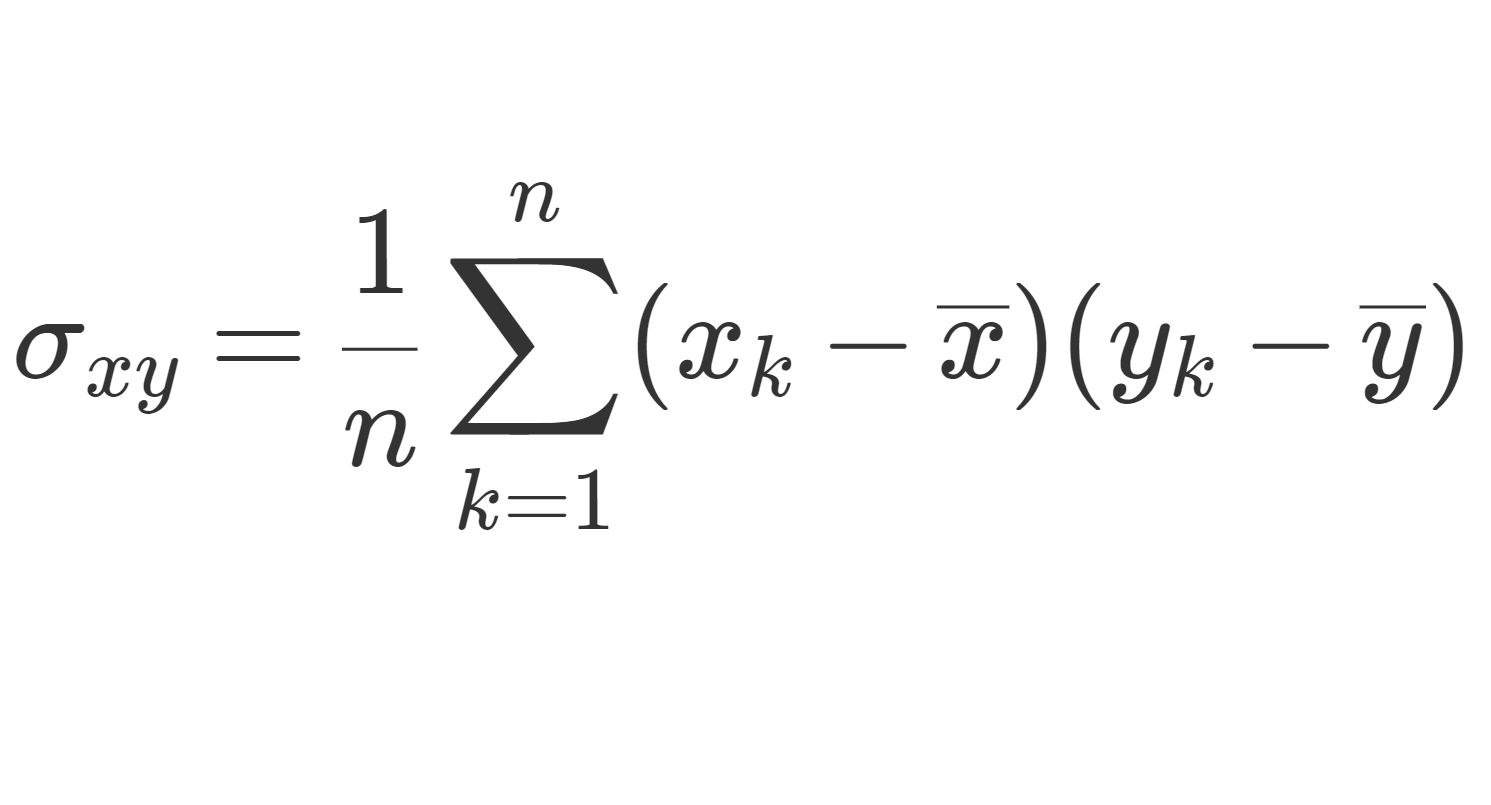相関係数の定義とデータの相関について,その定義からイメージ,よくある誤りや実際の求め方の例までを順番に詳しく解説しましょう。
相関係数とは
定義(相関係数)
データ (x_1,y_1),(x_2,y_2),\dots, (x_n,y_n) に対して, \overline{x},\overline{y} をそれぞれの平均,
\begin{aligned} \sigma_x &= \sqrt{\frac{1}{n} \sum_{k=1}^n (x_k-\overline{x})^2}, \\ \sigma_y &= \sqrt{\frac{1}{n} \sum_{k=1}^n (y_k-\overline{y})^2}, \\ \sigma_{xy} &= \frac{1}{n} \sum_{k=1}^n (x_k-\overline{x}) (y_k-\overline{y}) \end{aligned}
をそれぞれ x,y の標準偏差,(x,y) の共分散とする。このとき,
を (x,y) の相関係数 (correlation coefficient) またはピアソンの積率相関係数 (Pearson’s product-moment correlation coefficient) という。
定義を書き下すと
\begin{aligned}r &=\frac{\sigma_{xy}}{\sigma_x\sigma_y}\\ &= \frac{\frac{1}{n}\sum_{k=1}^n (x_k-\overline{x}) (y_k-\overline{y}) }{\sqrt{ \frac{1}{n} \sum_{k=1}^n (x_k-\overline{x})^2 }\sqrt{ \frac{1}{n} \sum_{k=1}^n (y_k-\overline{y})^2 }}\\ &= \frac{\sum_{k=1}^n (x_k-\overline{x}) (y_k-\overline{y}) }{\sqrt{ \sum_{k=1}^n (x_k-\overline{x})^2 }\sqrt{ \sum_{k=1}^n (y_k-\overline{y})^2 }} \end{aligned}
ですね。最後のイコールは分母分子から 1/n を取りました。
相関係数は常に \color{red} -1\le r\le 1 をみたします。これは,
\begin{aligned}\boldsymbol{x}&=(x_1-\overline{x}, \dots, x_n-\overline{x}), \\ \boldsymbol{y} &=(y_1-\overline{y}, \dots, y_n-\overline{y} )\end{aligned}
と,数ベクトルを用いて表記したときに, r = \dfrac{\langle \boldsymbol{x},\boldsymbol{y}\rangle}{\lVert \boldsymbol{x} \rVert \lVert \boldsymbol{x} \rVert } (分母はノルム,分子は内積) とかけるため,コーシーシュワルツの不等式から従います。
なお,相関係数は \sigma_x = 0 または \sigma_y=0 のときは定義できません。\sigma_x =0\iff x_1=x_2=\dots =x_n ですから,あまり気にする必要はないでしょう。
相関係数とデータの相関
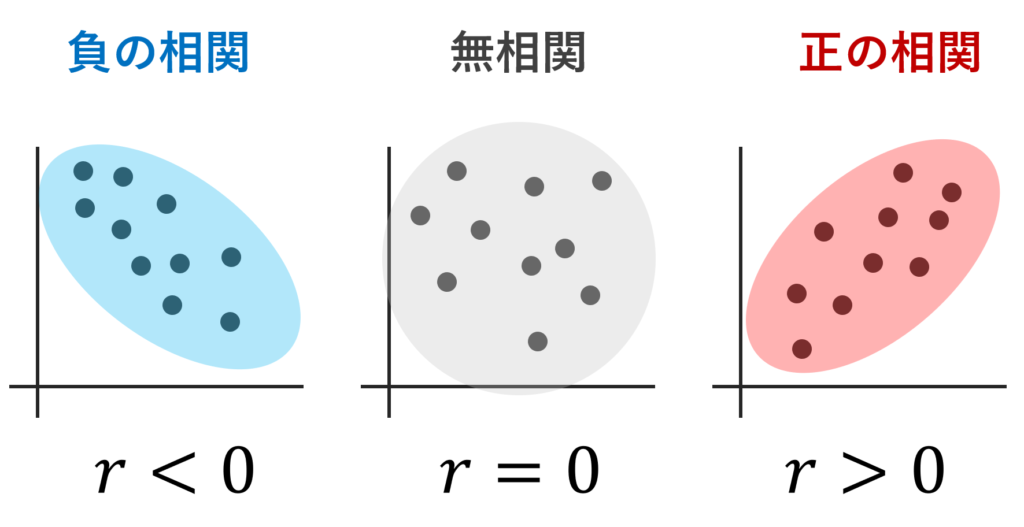
相関係数を用いることで,データが右上がりに分布しているか,右下がりに分布しているが大まかにわかります。このように, x が変化すれば y も変化する,y が変化すれば x も変化する関係を相関関係といいます。
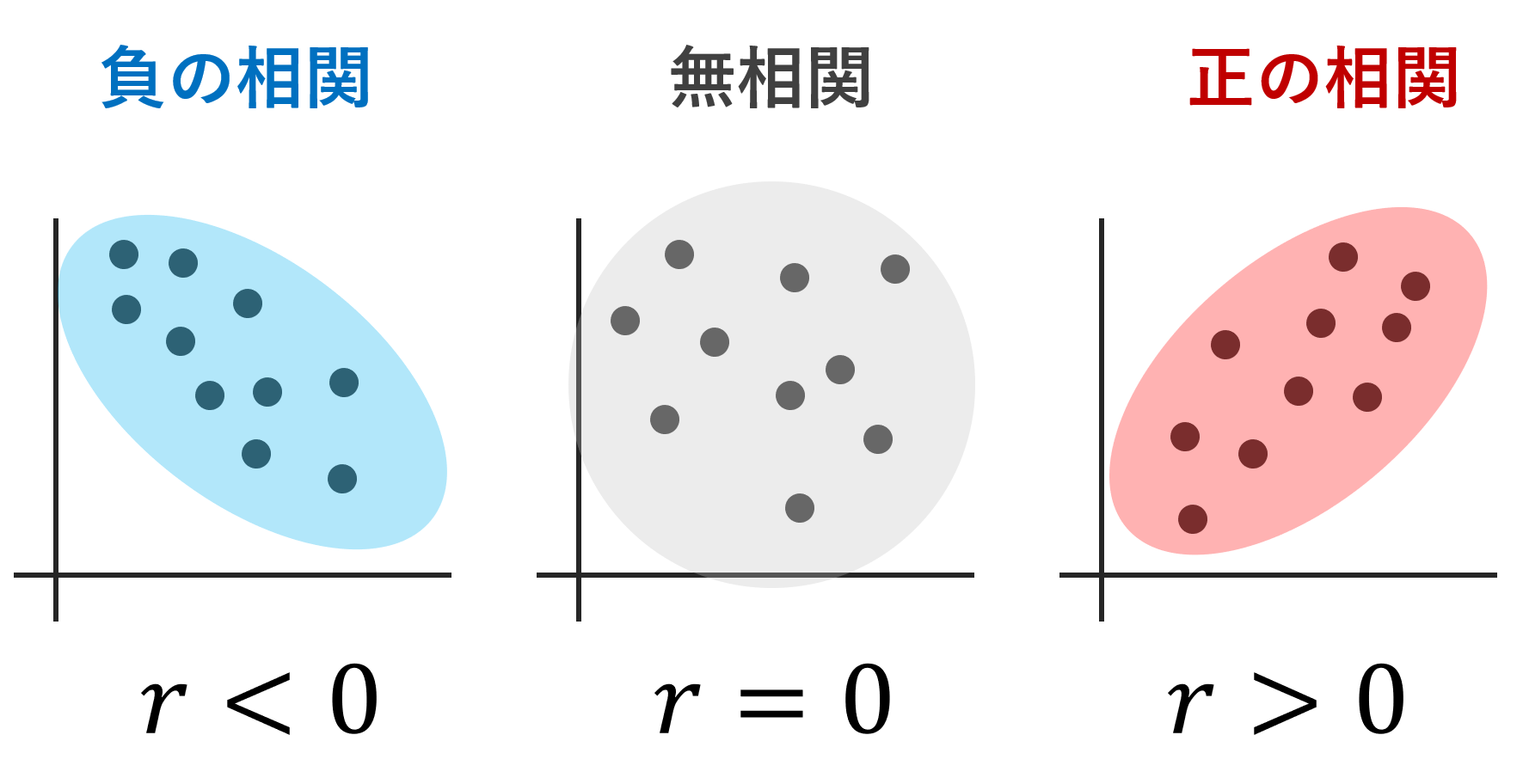
r>0 のとき正の相関, r<0 のときは負の相関があるといい, r=0 のときは無相関と呼ばれます。
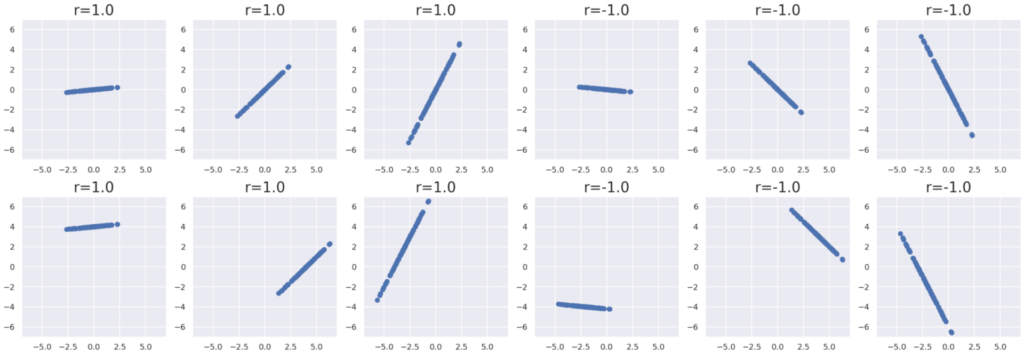
散布図と相関係数の大まかな対応と目安
散布図と相関係数 r の大まかな対応を確認しておきましょう。
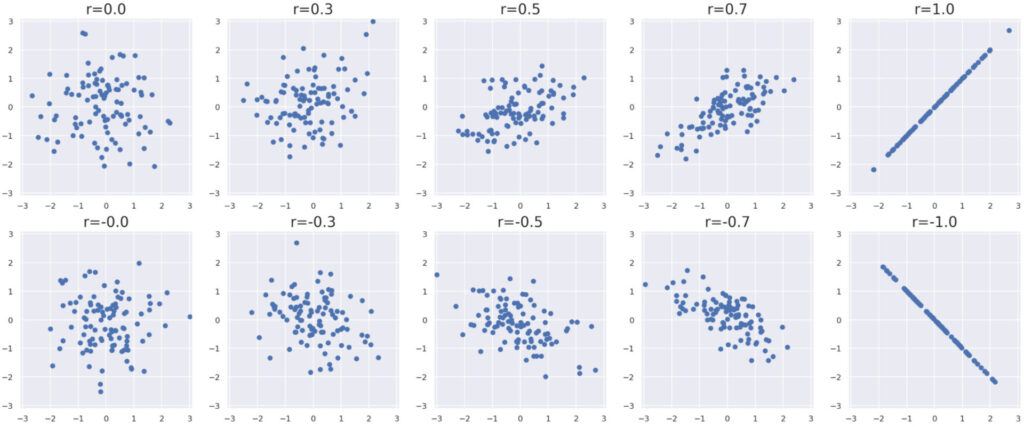
Wikipediaにある図も記しておきましょう。

このように,相関係数は散布図における直線的な関係性を表現可能です。
相関係数と概ねの相関の解釈は以下の通りです。
| 相関係数 | データの相関 |
|---|---|
| -1\le r\le -0.7 | 強い負の相関がある |
| -0.7\le r\le -0.4 | 負の相関がある |
| -0.4\le r\le -0.2 | 弱い負の相関がある |
| -0.2\le r\le 0.2 | ほとんど相関がない |
| 0.2\le r\le 0.4 | 弱い正の相関がある |
| 0.4\le r\le 0.7 | 正の相関がある |
| 0.7\le r\le 1 | 強い正の相関がある |
実際はデータ数によって相関があるといえるかどうかが変わってきます(無相関検定)。
なお, |r|=1 \iff データがちょうど一直線上です。このとき,直線の傾きの強さや,切片の値は関係ありません。相関係数は直線の傾き具合を表すわけではないことに注意しましょう。
相関係数は外れ値に大きく影響されることがある
相関係数は一つの外れ値に大きく影響されてしまうことがあります。以下の2つの図を見てください。
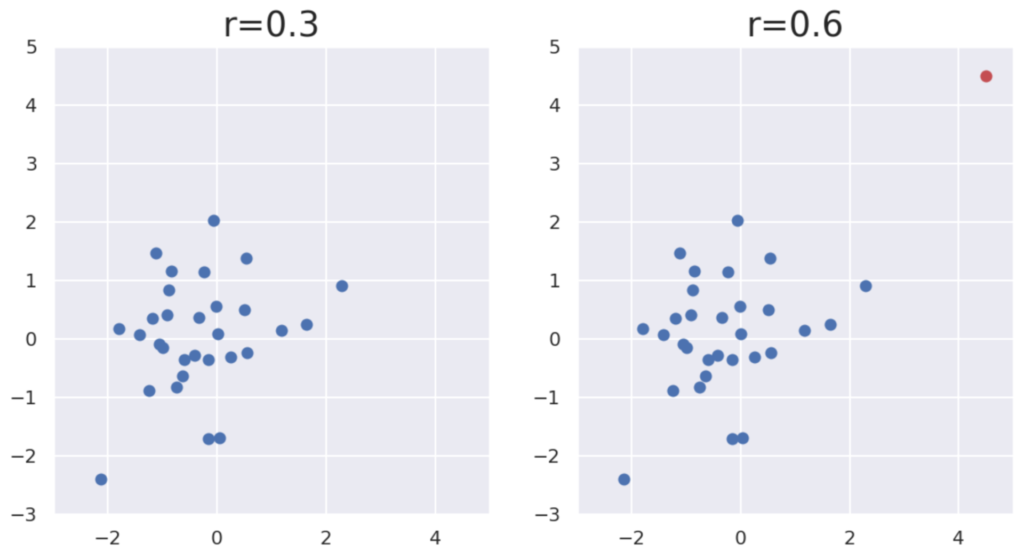
右の図は右上に赤の点があることが分かると思います。この点をデータに含めるかどうかで,相関係数は 0.3 から 0.6 に増えることが分かりますね。
このように,外れ値が一つあると相関係数が大きく変わってしまうことがあるため,実データを扱うときには注意が必要です。
相関関係があるからといって因果関係があるとは言えない
相関関係とは,あくまで「片方の値が変化すればもう片方の値も変化する」という関係であり,「原因と結果が明確」な因果関係ではありません。要するに,たとえば x の値が増えることが「原因」で y の値が増えるといった解釈はできません。
たとえば,一般にアイスの売り上げと日傘の売り上げは正の相関がありますが,アイスの売り上げが多いことが「原因」で日傘の売り上げが多くなるわけではありません。この場合,本当の原因は気温ですね。
このように,相関関係はあるが,直接的な因果関係がないと思えるものを擬似相関 (spurious relationship) といいます(相関関係はあることに注意)。
相関関係などから因果関係を探る理論は因果推論 (causal inference) とよばれます。
無相関だからといって独立とは言えない
先ほど,相関関係があるが因果関係があるとは言えないと述べました。では逆に無相関,すなわち r=0 であれば x,y は全く関係がないと言い切れるのでしょうか。
答えはNoです。以下の図を見てください。

無相関( r=0)とは,あくまでデータに直線的な関係がないことを意味します。一方で,上の図は x が決まれば y の値が制限されていますから, x,y が「全くの無関係」とは言えません。全くの無関係とは,確率の言葉でいうと「独立」ということです。
別の例も見てみましょう。The Datasaurus Dozen と呼ばれる有名な図です。

上図は, x,y の平均 (mean),標準偏差 (SD),相関係数 (Corr) が小数第二位まで一致しているにもかかわらず,全然違う散布図になっています。このようなことが可能とは驚きですね。
教訓としては,各平均や分散・相関係数が一致していたとしても,一度はきちんと散布図で可視化すべしということですね。
相関係数の求め方の具体例
最後に,相関係数の求め方を例題を通して紹介しておきましょう。
例題.
5人の数学・国語の点数は以下のとおりである。2つの点数の相関係数を求めよ。
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 数学 | 20 | 40 | 70 | 80 | 90 |
| 国語 | 10 | 50 | 40 | 60 | 90 |
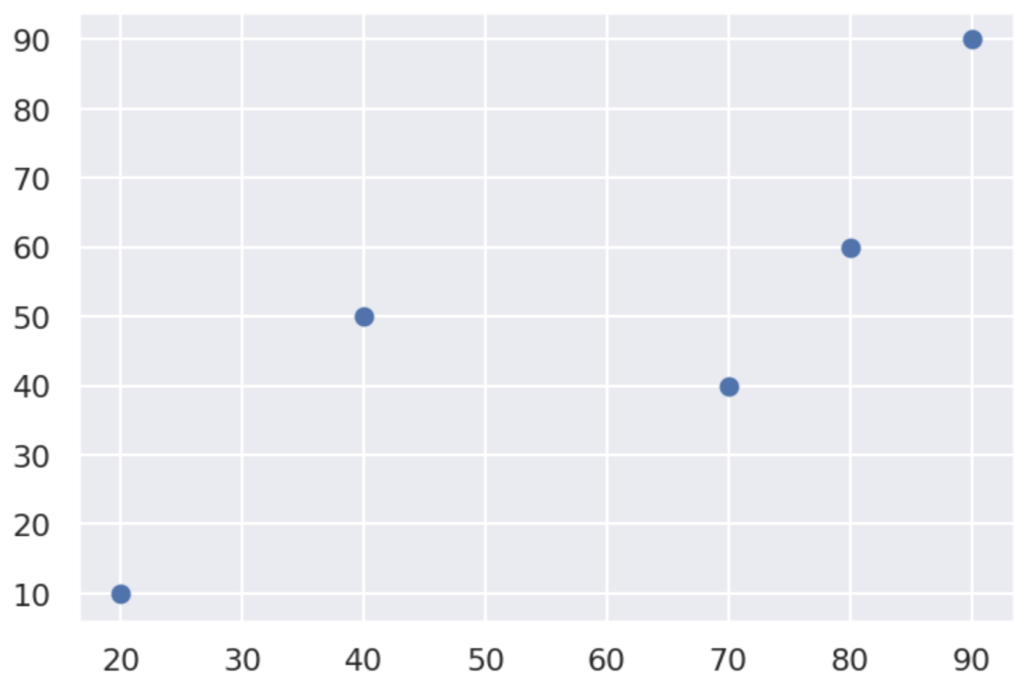
相関係数の定義から,
r =\frac{\sigma_{xy}}{\sigma_x\sigma_y}=\frac{\sum_{k=1}^n (x_k-\overline{x}) (y_k-\overline{y}) }{\sqrt{ \sum_{k=1}^n (x_k-\overline{x})^2 }\sqrt{ \sum_{k=1}^n (y_k-\overline{y})^2 }}
でしたから,右辺を計算しましょう。そのためには,順番に求めていくしかありません。表にするとわかりやすいでしょう。
| k | 1 | 2 | 3 | 4 | 5 | 平均または和 |
|---|---|---|---|---|---|---|
| x_k | 20 | 40 | 70 | 80 | 90 | \overline{x}= 60 |
| y_k | 10 | 50 | 40 | 60 | 90 | \overline{y}= 50 |
| x_k-\overline{x} | -40 | -20 | 10 | 20 | 30 | |
| y_k-\overline{y} | -40 | 0 | -10 | 10 | 40 | |
| (x_k-\overline{x})^2 | 1600 | 400 | 100 | 400 | 900 | \sum_{k=1}^5= 3400 |
| (y_k-\overline{y})^2 | 1600 | 0 | 100 | 100 | 1600 | \sum_{k=1}^5 = 3400 |
| (x_k-\overline{x})(y_k-\overline{y}) | 1600 | 0 | -100 | 200 | 1200 | \sum_{k=1}^5= 2900 |
よって,求める値は
r =\frac{2900}{\sqrt{3400}\sqrt{3400}} = \frac{29}{34} = 0.8529\cdots
となります。なお,今回は定義を用いて計算しましたが, \sigma_x = \overline{(x^2)}-(\overline{x})^2 や \sigma_{xy} = \overline{xy} - \overline{x}\,\overline{y} を用いても構いません。