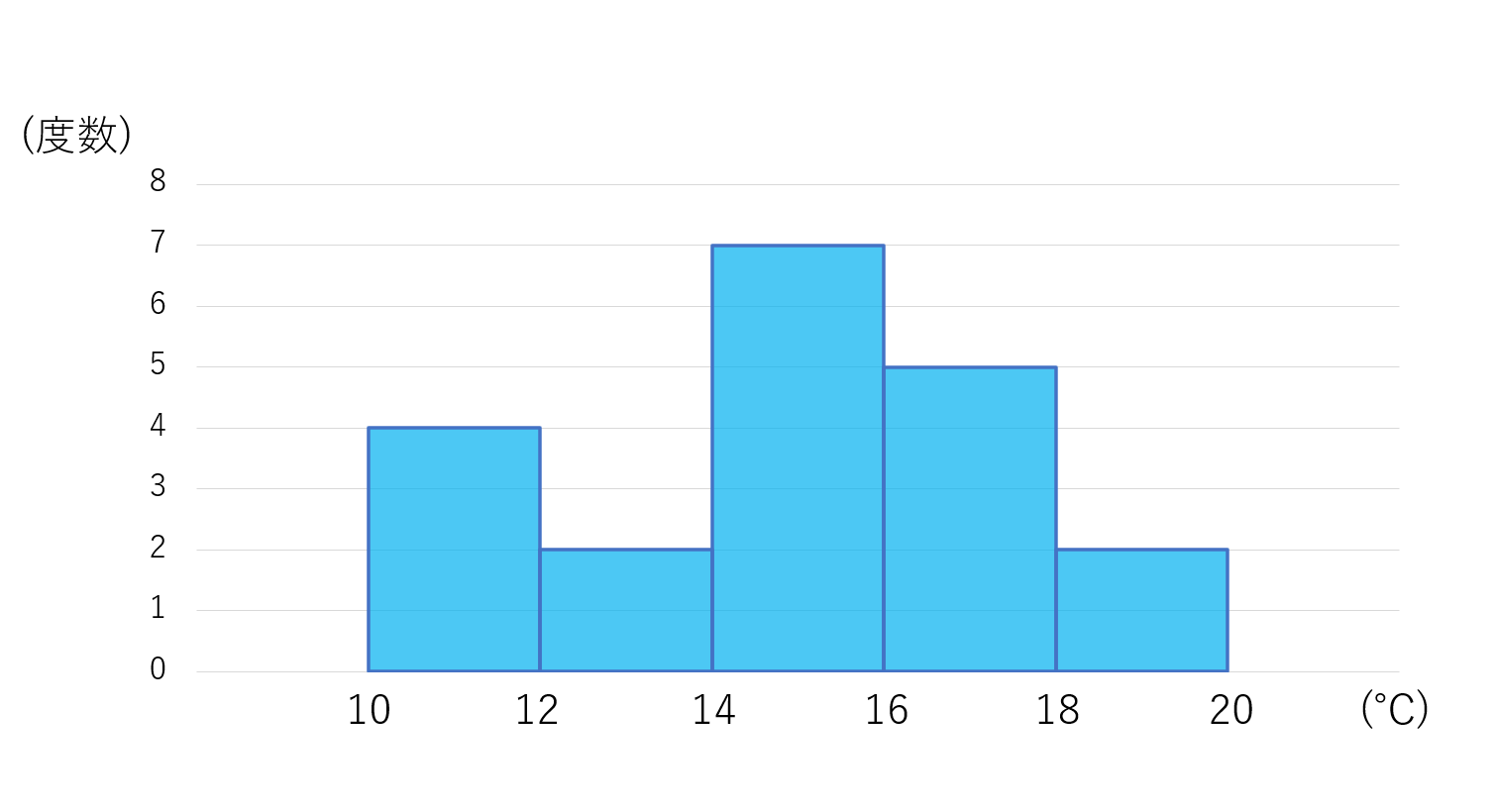統計学における,データをまとめる手法として「度数分布表」と,その関連用語を図を使って紹介しましょう。
度数分布表とは
定義(度数分布表)
データをある範囲ごとに区切って,その範囲に属する数の散らばりの様子を度数分布 (frequency distribution) といい,それを表にしたものを度数分布表 (frequency table) という。
このとき,区切られた各区間を階級,各区間の幅を階級幅,各階級の真ん中の値を階級値,各階級に属するデータの数を度数 (frequency) という。
さらに,各階級の度数を全体における割合で表したものを相対度数という。ある階級以下の度数を全て足したものを累積度数といい,それを全体における割合で表したものを累積相対度数という。
定義を見ただけでは難しいですから,図解しましょう。まず,以下のようなデータ (data)があったとします(偽物のデータです。これは度数分布表ではありません)。
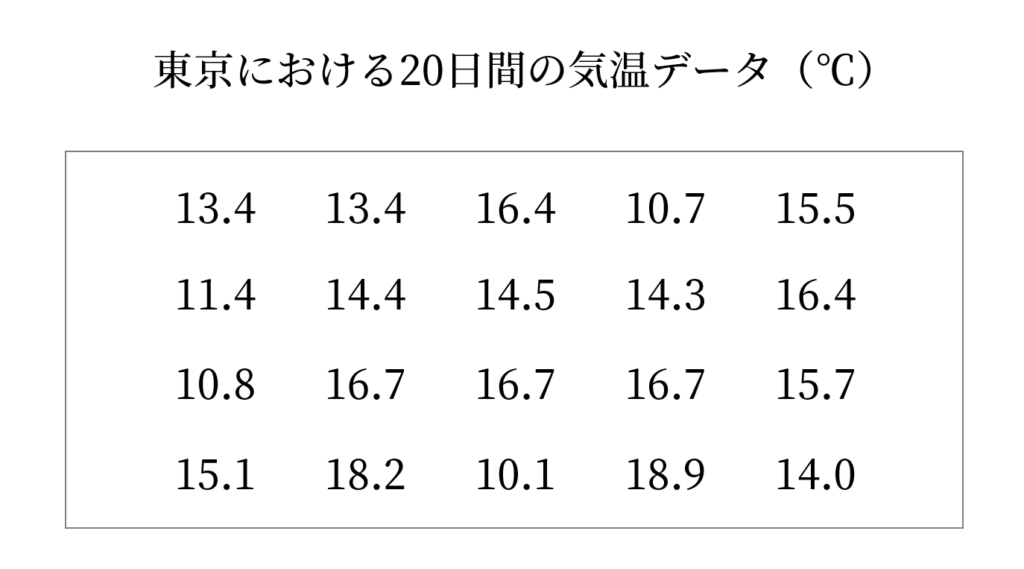
20日分のデータがありますから,データの大きさは20といい,一つ一つの値を変量といいます。
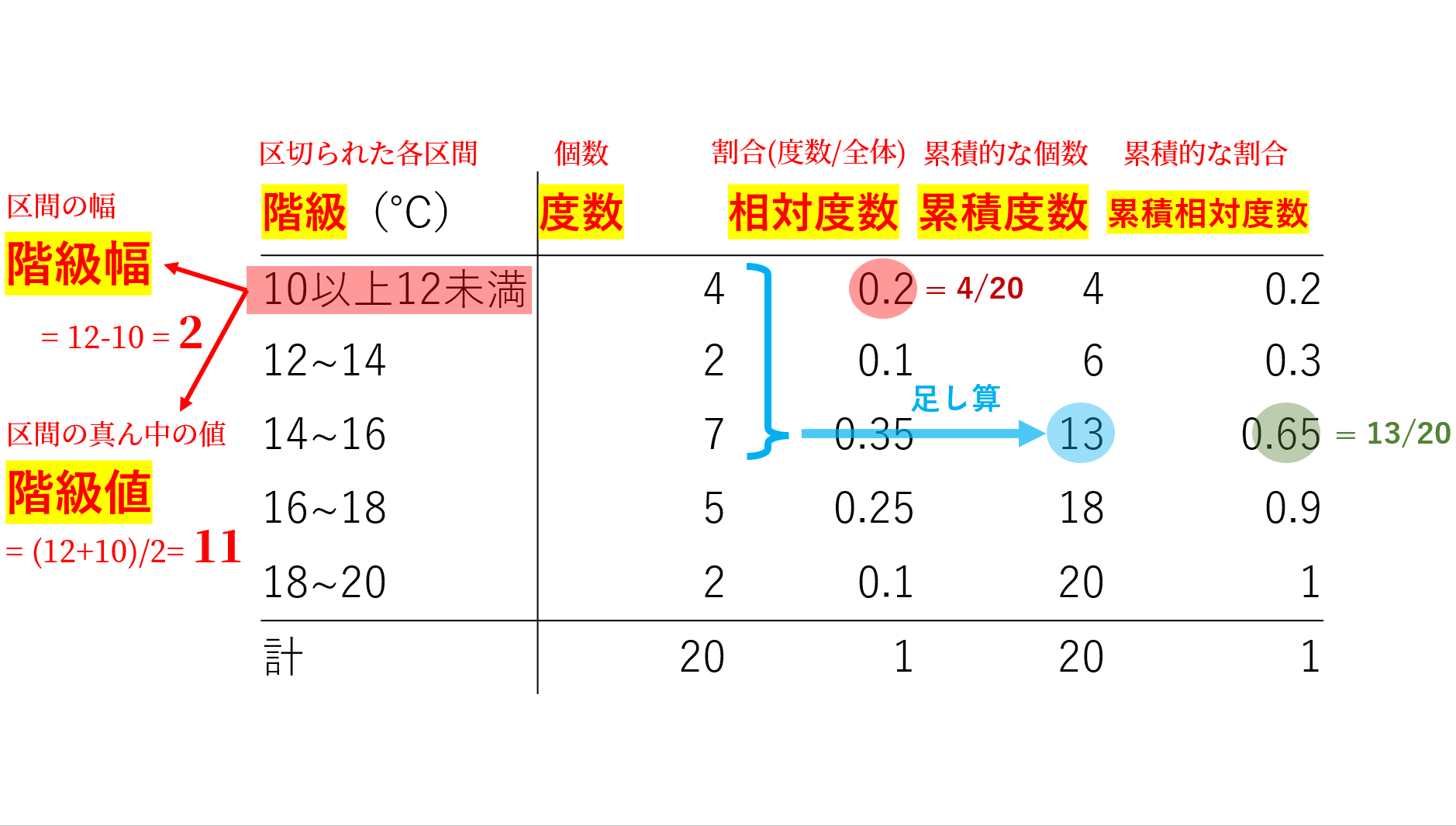
このデータを範囲を区切って,度数分布表をかいたのが以下です。相対度数や累積度数は書かないことも多いですが,今は含めています。
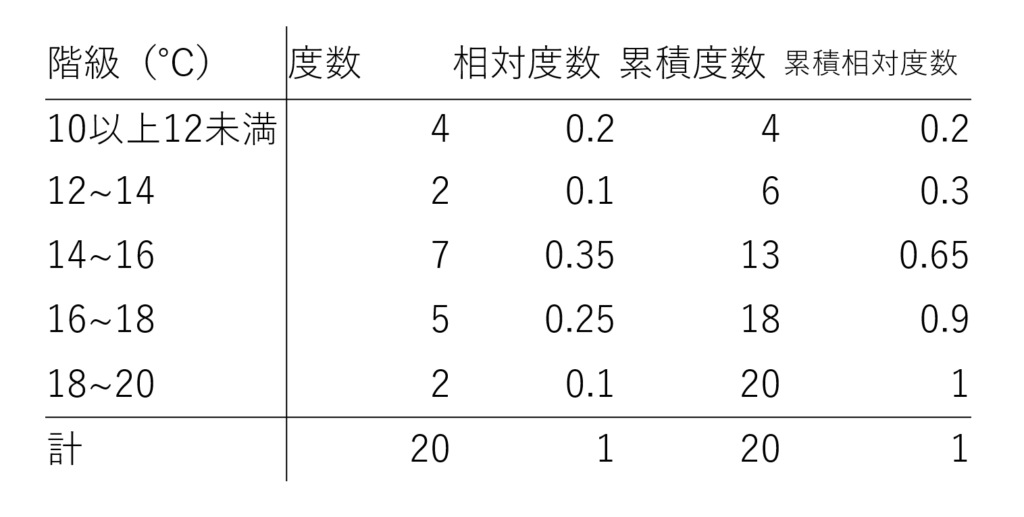
順番に解説しましょう。まず,度数とは「範囲に入る変量の数」でしたから,地道に個数を数えてあげることで,以下のように定まります。これだけでも立派な度数分布表です。
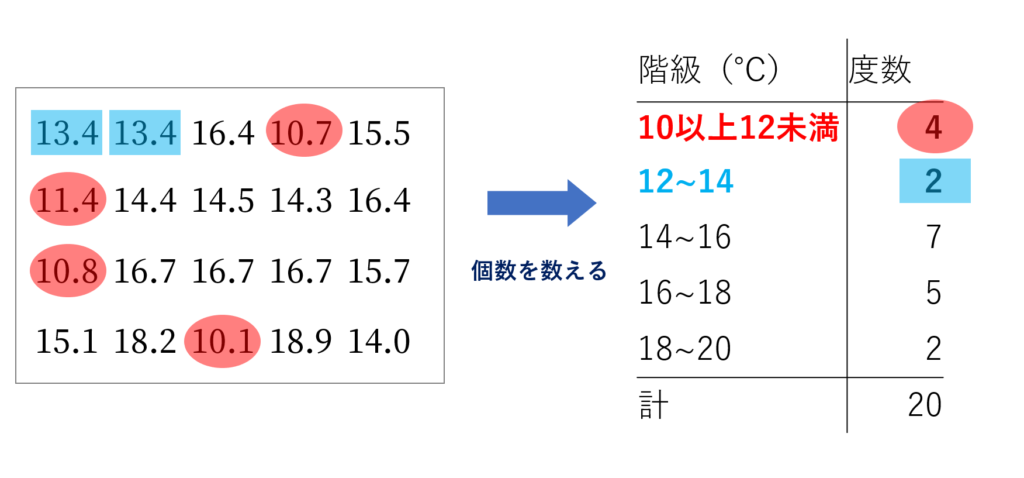
それをもとに,残りは計算すれば定まりますね。
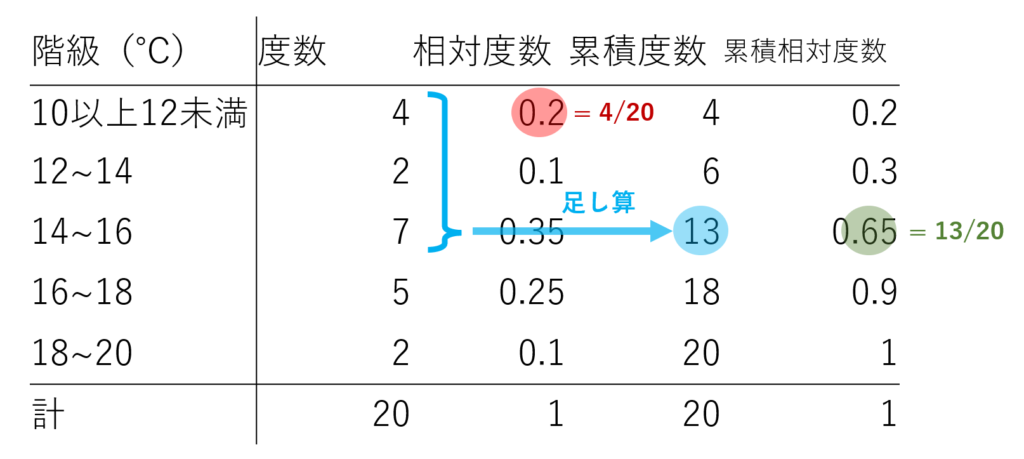
各用語の解説を赤字で表に加えると,以下のようになります。この表を覚えてしまってもいいかもですね。
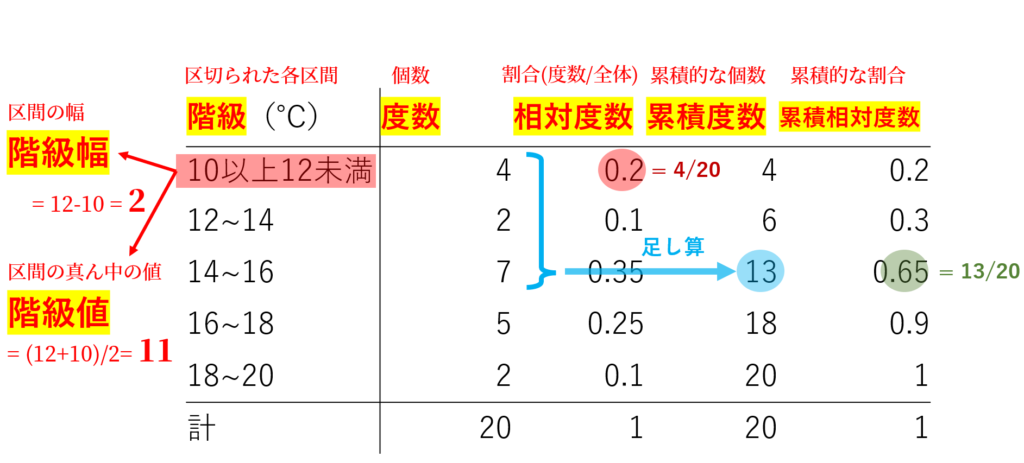
今回は「気温データ」を例にしましたが,各生徒のテストの成績や,各生徒の50m走のタイム, n 択アンケートの集計など,さまざまなものを度数分布表にすることが可能です。
度数分布表は,元の詳細なデータは無視していますが,データをざっくり区切ることで,おおよその分布を知ることができます。データを把握するのに有効なツールの一つです。
ヒストグラム
度数分布表を柱状のグラフで表したものもヒストグラム (histogram) といいます。度数分布表は「表」ですから,それをグラフにした方が見やすいという考えですね。これについては以下で解説しています。