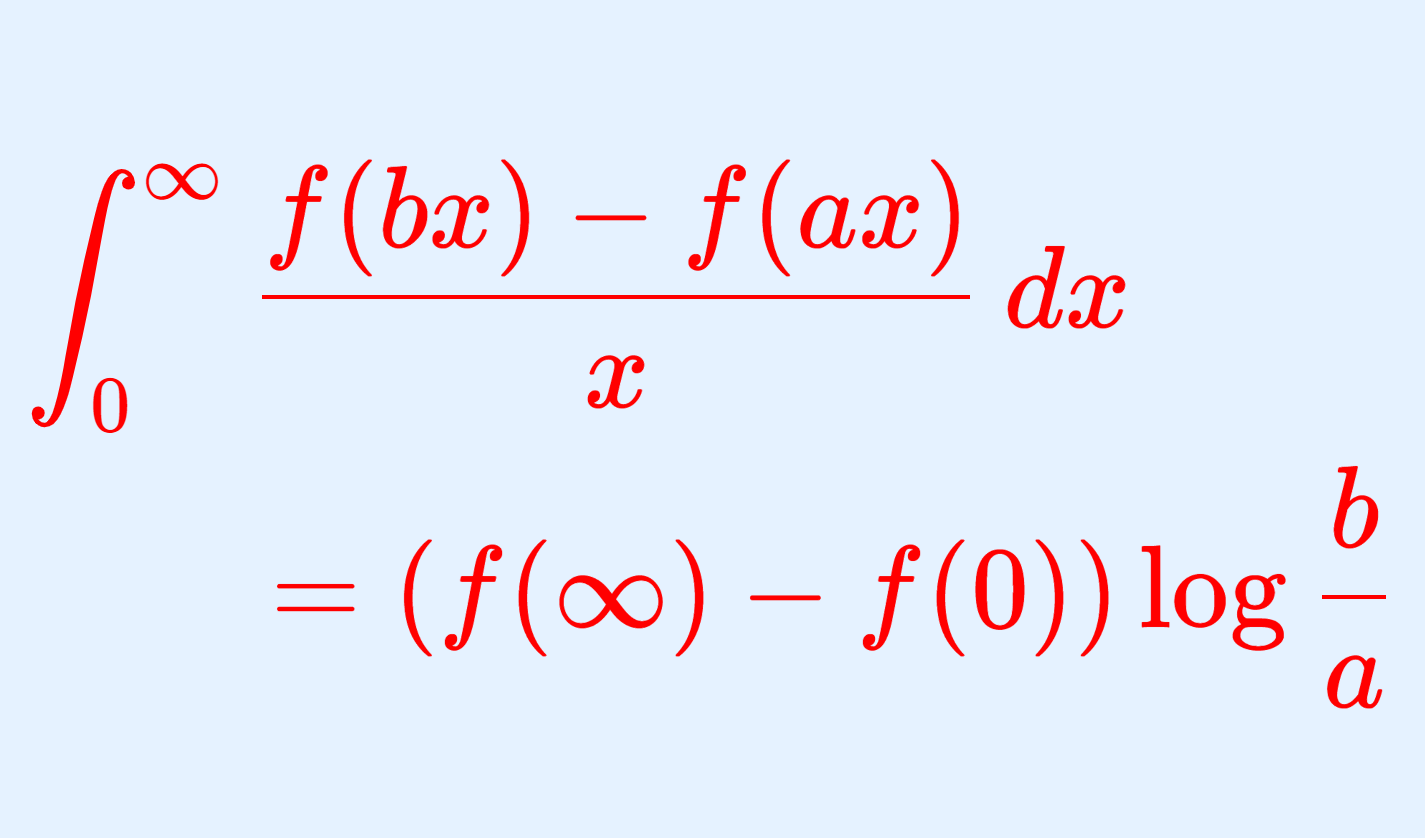Frullani 積分 (Frullani integral) について,その主張を紹介し,証明します。
Frullani integralの主張
定理(Frullani’s integral)
f\colon [0,\infty) \to \mathbb{R} を C^1 級関数(すなわち微分可能で導関数が連続)とし,さらに f(\infty) = \lim_{x\to\infty} f(x) が収束するとする。
このとき, 0 < a < b に対し,
が成立する。
C^1 級関数の意味について,もし分からない場合は,C1級,Cn級,C∞級関数の定義と具体例5つを参照してください。
早速証明しましょう。
Frullani integralの証明
証明
c>0 とする。
\begin{aligned} \int_0^c \frac{f(bx) - f(ax)}{x} \, dx &= \int_0^c \int_a^b f^\prime(tx) \, dt dx. \\ \end{aligned}
フビニの定理より,積分の順序を交換して,
f は [0, \infty) 上有界であるから, |f(x)|<M \,\, (0\le x< \infty) となる M>0 を取る。すると, |(f(tc)-f(0))/t| \le 2M/t であり,右辺は [a,b] 上可積分であるから,ルベーグの収束定理より,
よって,
\begin{aligned}
& \int_0^\infty \frac{f(bx) - f(ax)}{x} \, dx \\
&\qquad = (f(\infty) -f(0))\log\frac{b}{a}
\end{aligned}
である。
証明終
証明できましたね。フビニの定理を使う際に,積分の絶対収束性が要るのですが,そこで f' の連続性を用いて,有界領域内で重積分が絶対収束するようにしています。
Frullani integralの例
一つだけ例を挙げましょう。
例
0<a<b に対し,
\color{red} \int_0^\infty \frac{e^{-bx} - e^{-ax}}{x} \, dx = \log\frac{b}{a}.