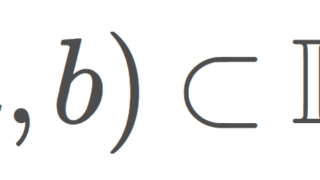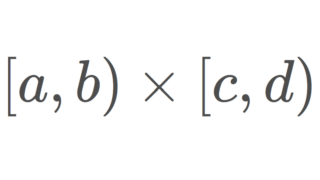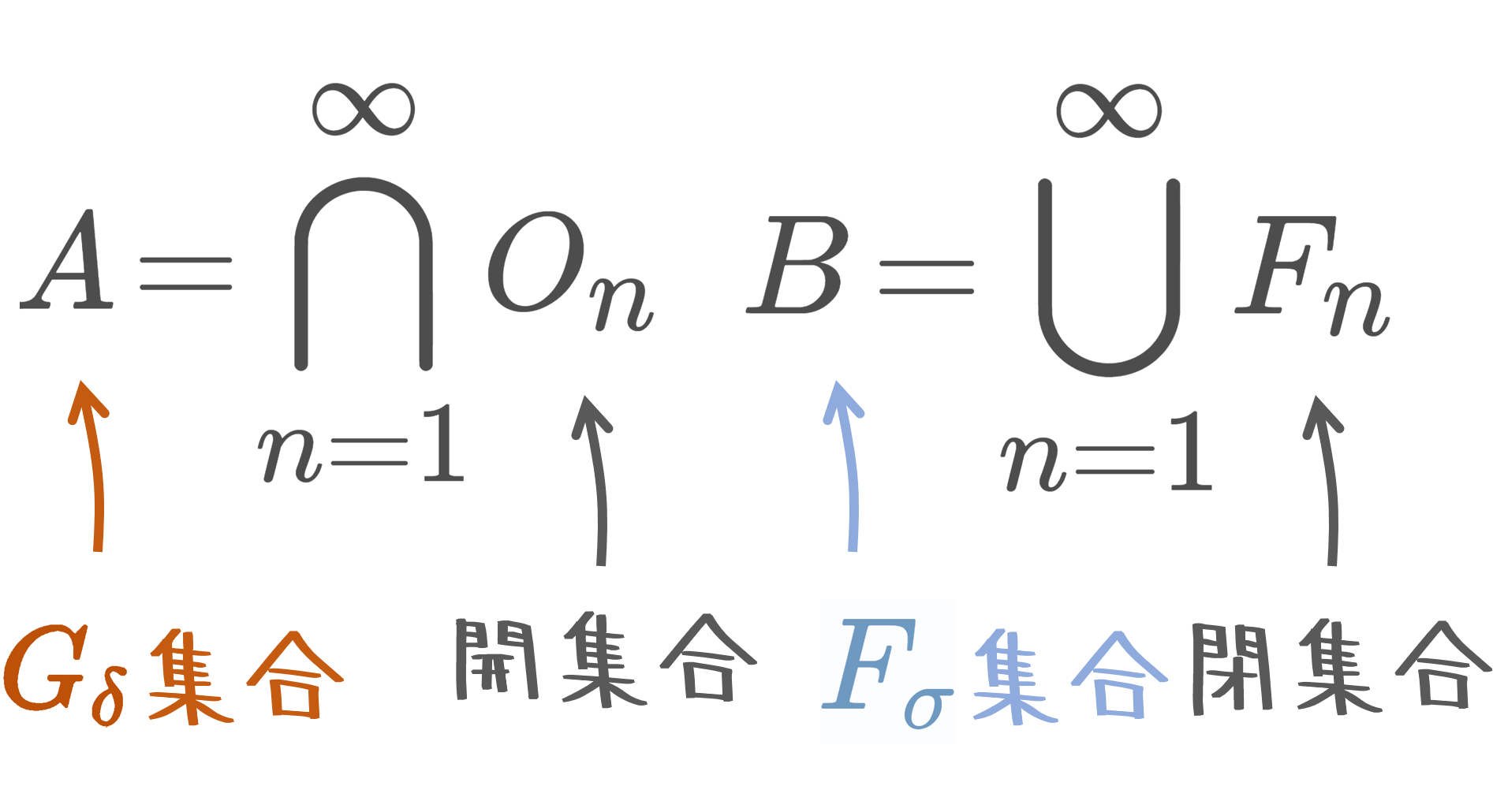リンデレーフ空間(リンデレフ空間)とは,任意の開被覆が可算部分被覆をもつような位相空間のことです。コンパクトが「任意の開被覆が有限部分被覆をもつ」だったので,「有限」の部分を「可算」に弱めたのがリンデレーフだといえます。
リンデレーフ空間と,さらに強い意味の遺伝的リンデレーフ空間について,その定義と性質・具体例を紹介しましょう。
リンデレーフ空間・遺伝的リンデレーフ空間

定義(リンデレーフ空間・遺伝的リンデレーフ空間)
(X,\mathcal{O}) を位相空間とする。
X の任意の開被覆 \mathcal{C} に対し,可算部分被覆 \mathcal{C}_0\subset \mathcal{C} が存在するとき, (X,\mathcal{O}) はリンデレーフ空間 (リンデレフ空間; Lindelöf space) であるという。
さらに,任意の部分空間がリンデレーフとなるような位相空間 (X,\mathcal{O}) を遺伝的リンデレーフ空間 (hereditarily Lindelöf space)または強リンデレーフ空間 (strongly Lindelöf space)という。
任意の開被覆が,有限部分被覆をもつのが,コンパクト (compact) の定義ですから,それを弱めたのがリンデレーフ (Lindelöf) の定義です。特に,コンパクトならばリンデレーフです。
「開被覆」や「部分被覆」という言葉の意味が分からない場合は,まずはコンパクトの記事を見てください。コンパクトの記事中で解説しています。
リンデレーフ空間の性質
定理(リンデレーフ空間の性質)
- リンデレーフ部分空間の可算和はまたリンデレーフである
- リンデレーフ空間の閉部分集合はリンデレーフである
- リンデレーフ空間の連続写像の像もまたリンデレーフである
- σコンパクト空間はリンデレーフである。また,リンデレーフかつ局所コンパクトな空間はσコンパクトである。ただし,局所コンパクトとは,任意の点がコンパクトな近傍を持つことをいう
- 第二可算公理をみたす空間は可分かつ遺伝的リンデレーフである。また,距離空間においては,第二可算公理をみたすこと・可分であること・リンデレーフであることが同値になる
- リンデレーフ空間の直積空間は,(有限個の直積であっても)リンデレーフとは限らない
- リンデレーフであることと,可算交叉性をもつ閉集合族が交叉することは同値である
ただし後半は,位相空間 (X,\mathcal{O}) の部分閉集合族 \mathcal{D} に対し,任意の可算部分集合 \mathcal{D}_0\subset \mathcal{D} で \bigcap_{D\in\mathcal{D}_0} D\ne\emptyset が成り立つなら, \bigcap_{D\in\mathcal{D}} D\ne \emptyset が成り立つことをいう - リンデレーフ空間がコンパクトであることと,可算コンパクトであることは同値である
2.について,閉部分集合であることがポイントで,閉でないときはリンデレーフとは言えません。閉でなくてもリンデレーフが言えるのが,遺伝的リンデレーフ空間です。
1, 2, 3, 7.の証明は,コンパクトのときとほぼ同じです。コンパクトのときの証明における「有限」の部分を「可算」に書き換えるだけです。よって,省略します。コンパクトのときの証明は,コンパクト空間とコンパクト集合について詳しくを参照してください。
4.の証明は,σコンパクト空間の定義・性質・具体例を詳しくにあります。σコンパクトとは,コンパクト集合の可算和で表される空間のことです。
5.について,第二可算公理をみたす空間の部分空間は,また第二可算公理をみたしますから,「第二可算ならばリンデレーフ」が言えれば,「第二可算ならば遺伝的リンデレーフ」も示せたことになります。5.については,第二可算公理と第二可算な位相空間の例・性質で証明しています。
6.については,コンパクト空間の直積が常にコンパクトであるというチコノフの定理 (Tychonoff’s theorem)とは対照的です。ゾルゲンフライ直線とゾルゲンフライ平面が良い例です。【位相空間】ゾルゲンフライ平面の定義と性質を参照してください。後の例5.でも紹介します。
8.を示しましょう。可算コンパクト (countably compact) とは,「任意の可算開被覆が有限部分被覆をもつ」ことをいいます。コンパクトならば可算コンパクトであることはいいので,その逆を考えます。 \{U_\lambda\} を任意の開被覆とすると,リンデレーフ性より,可算部分被覆が存在します。すると,可算コンパクト性により,さらに有限部分被覆が存在することになり,コンパクトだと言えました。
リンデレーフ空間の具体例
例3(離散位相).
離散空間 (X,2^X) がリンデレーフである必要十分条件は, X が高々可算集合であることである。このとき,遺伝的リンデレーフである。
また,任意の有限集合・可算集合は位相に依らず遺伝的リンデレーフである。
例4(補可算位相).
X を非可算集合とし,
\mathcal{O}_c=\{\emptyset \}\cup \left\{O\subset X\middle|\begin{gathered} X\setminus O \text{ is at most} \\ \text{countable}\end{gathered}\right\}
を,補集合が高々可算集合である部分集合全体(と \{\emptyset\} との和集合)とすると, (X,\mathcal{O}_c) は位相空間になる。この位相を補可算位相 (cocountable topology, countable complement topology) という。
(X,\mathcal{O}_c) はコンパクトでも局所コンパクトでもない。σコンパクトでもない。第二可算公理もみたさない。しかし,遺伝的リンデレーフではある。
まず,リンデレーフ空間であることを示しましょう。 \{U_\lambda\}\subset\mathcal{O}_c を X の開被覆とすると, X\setminus U_\lambda は可算集合なので, \{x_1, x_2,\ldots\} =X\setminus U_\lambda とできます。各点 x_i の被覆 U_i をとってくれば, \{U_\lambda, U_1, U_2, \ldots\} は可算部分被覆になるため,リンデレーフです。
また,部分空間 A\subset X が非可算であるときは同じ議論によりリンデレーフだし,可算集合のときは離散空間になりますが, それもまたリンデレーフです。任意の部分空間がリンデレーフなので, (X,\mathcal{O}_c) は遺伝的リンデレーフといえます。
その他の性質について,詳しくは以下で解説しています。
例5(ゾルゲンフライ直線・ゾルゲンフライ平面).
実数全体の集合 \R に対し,
\mathcal{B}_l=\{ [a,b)\subset \R\mid a<b\}
を開基とする位相 \mathcal{O}_l を下限位相 (lower limit topology, right half-open interval topology) といい,位相空間 (\R, \mathcal{O}_l) をゾルゲンフライ直線 (Sorgenfrey line) という。
(\R,\mathcal{O}_l) はコンパクトでも局所コンパクトでもない。σコンパクトでもない。第二可算でもない。しかし,遺伝的リンデレーフではある。
また,その直積 (\R,\mathcal{O}_l)\times (\R,\mathcal{O}_l) はリンデレーフでもない。これを,ゾルゲンフライ平面 (Sorgenfrey plane) という。
ゾルゲンフライ直線がリンデレーフであることを示すのは少々大変です。リンデレーフであることは,以下で証明しています。以下の記事内における証明は,そのまま部分空間に適用しても大丈夫なので,遺伝的リンデレーフであることも言えます。
ゾルゲンフライ平面については,以下で解説しています。
例6(除外点位相).
X を空でない集合とし, p\in X とする。
\mathcal{O}_{\neg p} =\{X\}\cup \{ O\subset X\mid p\notin O\}
を, p を含まない部分集合全体の集合(と全体集合の和集合)とすると,(X,\mathcal{O}_{\neg p}) は位相空間となる。この位相を除外点位相 (excluded point topology) という。
(X,\mathcal{O}_{\neg p}) はコンパクトなので,リンデレーフであるが, X が非可算集合のとき,遺伝的リンデレーフではない。
X の開被覆には,絶対に X が含まれていないといけないので,コンパクトになります。一方で X が非可算集合のとき,部分空間 X\setminus \{p\} は非可算な離散空間になるため,リンデレーフではありません。
除外点位相のその他の性質は,以下で解説しています。
コンパクト性に関する諸概念
コンパクト性に関連する概念をまとめておきましょう。
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| 強局所コンパクト (stronlyg locally compact) | 任意の点がコンパクトな閉近傍をもつ |
| 相対コンパクト (relatively compact) | 閉包がコンパクトな部分集合 |
| 可算コンパクト (countably compact) | 任意の可算開被覆が有限部分被覆をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 極限点コンパクト (limit point compact) | 任意の無限部分集合が集積点をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち,各点ごとに有限個の集合でしか覆われていない)開細分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち,各点ごとに有限個の集合でしか覆われていない近傍をもつような)開細分被覆をもつ |