【対数グラフ】片対数グラフ・両対数グラフとその意味

グラフを描くにあたって，しばしば用いられる，片方の軸が対数に対応する目盛である「片対数グラフ」と，両方の軸が対数に対応する目盛である「両対数グラフ」について紹介し，このグラフ上で直線になるような関数はどのようなものか解説します。

【対数グラフ】片対数グラフ・両対数グラフとは

定義（片対数グラフ・両対数グラフ）

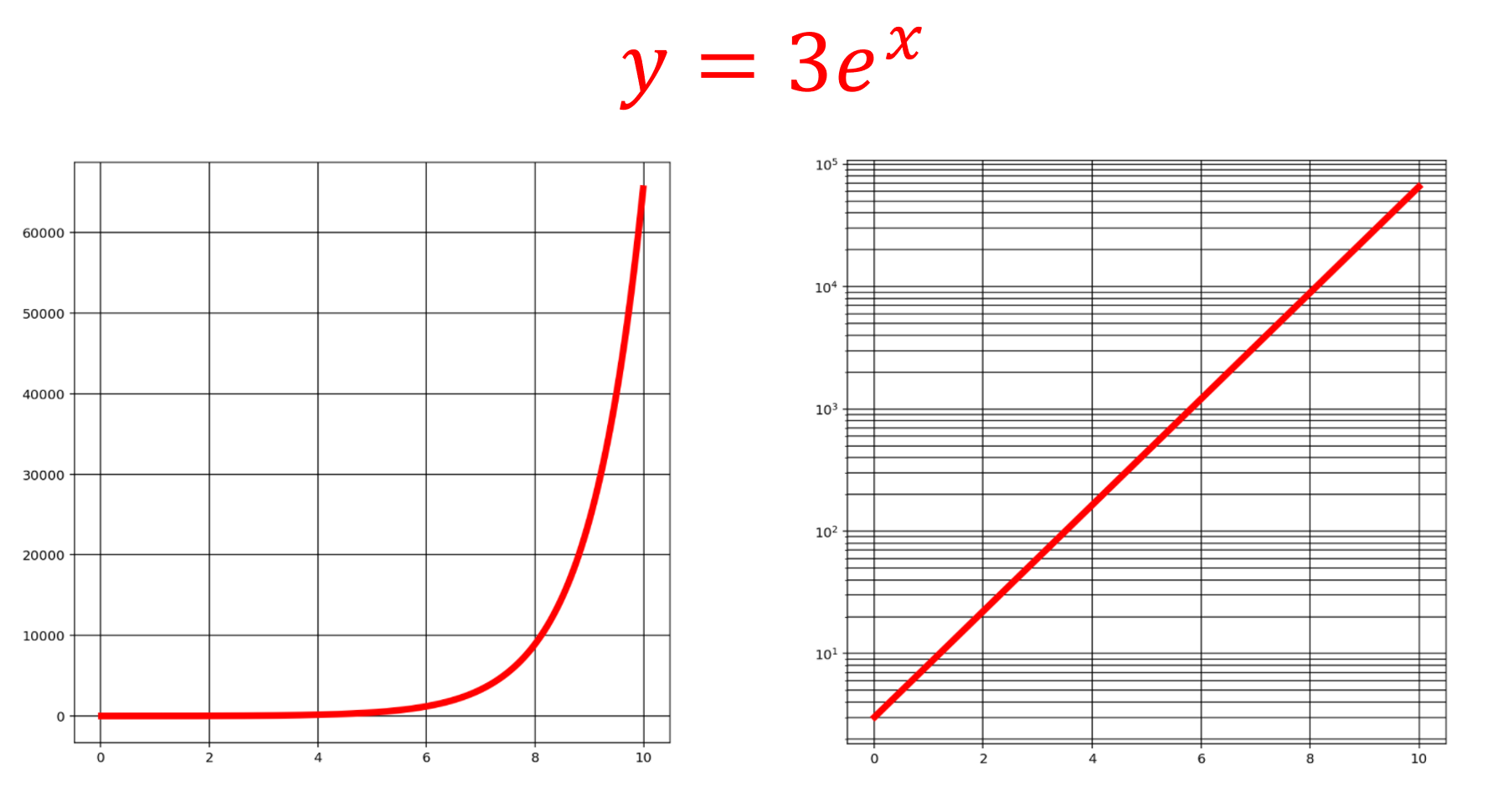
片方の軸が $\log_{10}$ スケールである，以下のようなグラフを片対数グラフ (semi-log plot) という。

両方の軸が $\log_{10}$ スケールである，以下のようなグラフを両対数グラフ (log-log plot) という。

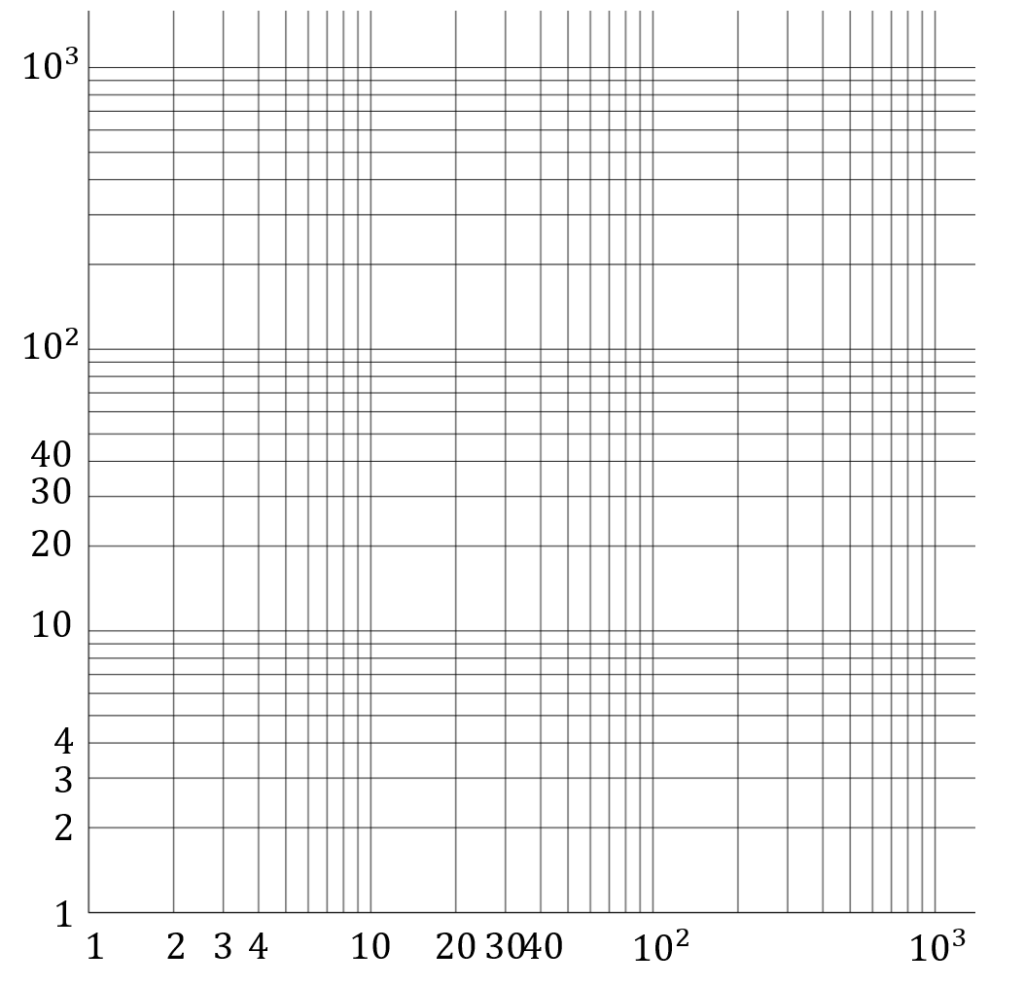
普通の目盛の方は，等間隔に並んでいますが，対数目盛の方は， $\log_{10} y$ が等間隔になるように目盛が並んでいます。( $x$ 軸の方が対数目盛でも構いません。)

従って，対数目盛においては，等間隔に目盛を $1$ ずつ進めていくと，等倍されていきます。

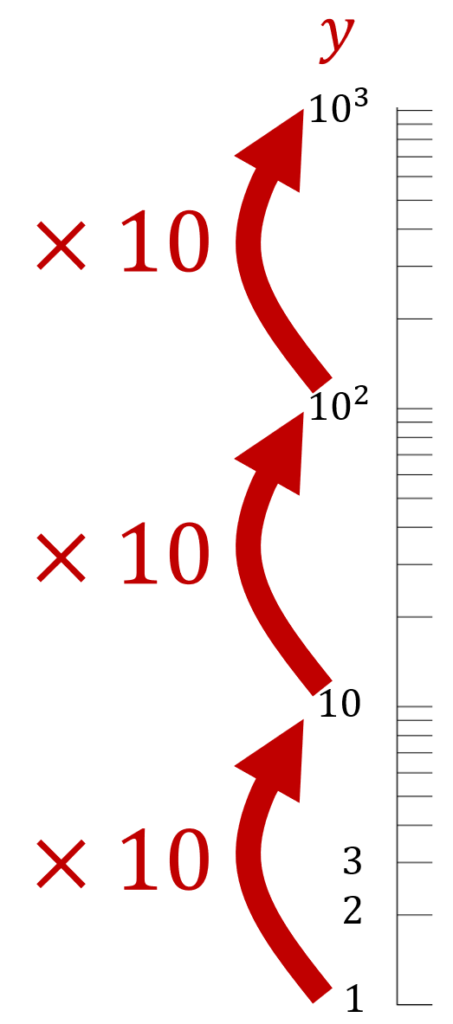
なお，対数目盛の方は， $0$ を取ることができません。下のように， $0$ に限りなく近づけることはできますが， $0$ に到達することはできませんね。

今回，片対数グラフ・両対数グラフは「統計学」のカテゴリーに入れましたが，物理や化学でもよく使われます。

対数グラフは何のためにあるのでしょうか。散布図をかいて，それを近似したい場面を考えましょう。

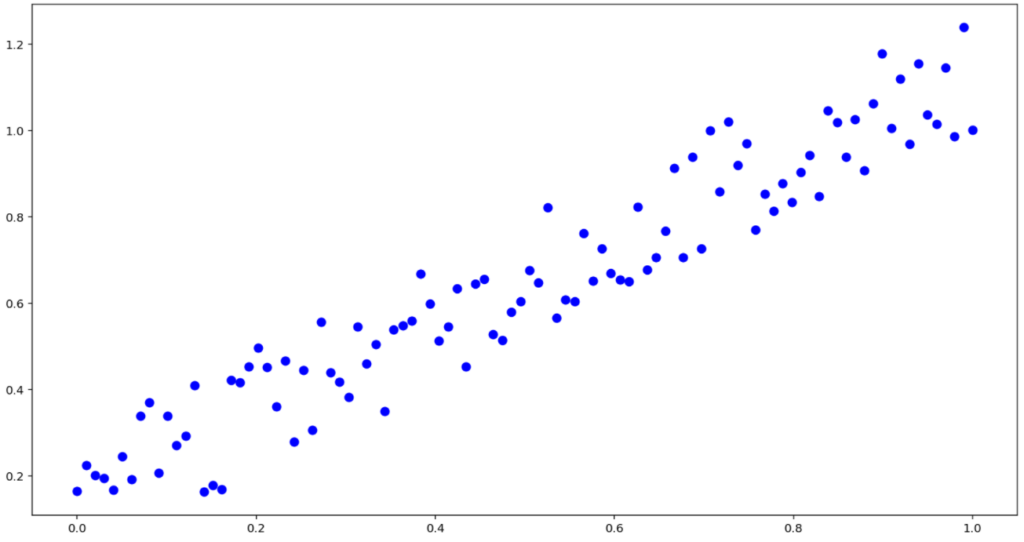
近似するには，直線を用いるのが最も分かりやすいでしょう。

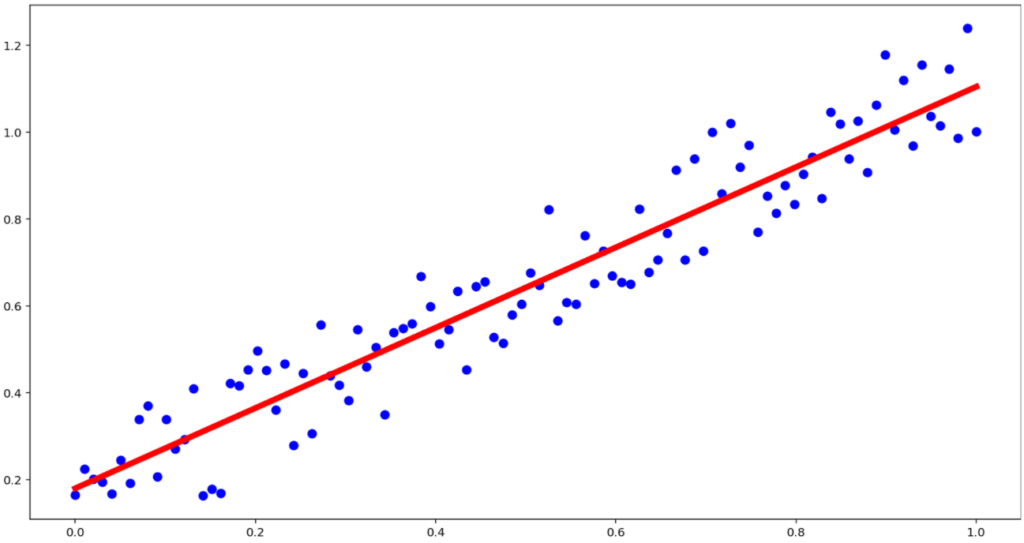
このように，「直線で近似する」という操作は，近似において基本的です。片対数グラフ・両対数グラフ上の散布図でも，直線で近似したいという思いがあります。

これは逆に，もともと直線でないものを，対数目盛を用いることで，直線近似可能になるようにする，という見方も可能です。

それでは，どのような関数が，片対数グラフ・両対数グラフで直線になるのか考えましょう。

定理（片対数グラフ・両対数グラフにおける直線の意味）

$y$ 軸が $\log_{10}$ スケールである片対数グラフにおける直線は，指数関数を表す。すなわち，片対数グラフの軸を $X,Y$ とすると，

\color{red} Y=AX+B \iff y = ce^{ax}.

ただし， $a = A\log 10 ,\; c =10^B$ とした。

両対数グラフにおける直線は，べき乗関数を表す。すなわち，両対数グラフの軸を $X,Y$ とすると，

\color{red} Y=AX+B\iff y= c x^A.

ただし， $c=10^B$ とした。

確認していきましょう。

片対数グラフの軸を $X, Y$ とし，元のグラフの変量を $x,y$ とすると， $X=x,\; Y=\log_{10}y$ ですから，

\begin{aligned}Y=AX+B &\iff \log_{10}y = Ax+B \\ &\iff 10^{ \log_{10}y } = 10^{Ax+B} \\ &\iff y = 10^B 10^{Ax} \end{aligned}

となります。 $a = A\log 10 ,\; c =10^B$ と定めることで， $y=ce^{ax}$ になり，確かに指数関数になりますね。

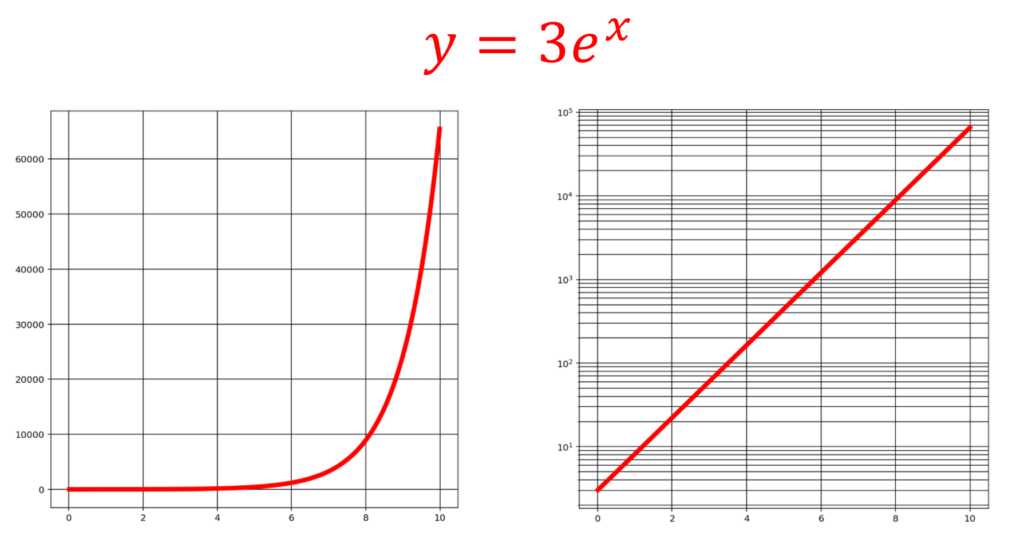
指数関数で近似したいものを片対数グラフで直線近似することで，指数関数で近似した際のパラメータ $a,c$ を求めることができるわけです。

両対数グラフの軸を $X, Y$ とし，元のグラフの変量を $x,y$ とすると， $X=\log_{10}x, \;Y=\log_{10}y$ ですから，

\begin{aligned}Y=AX+B &\iff \log_{10}y = A\log_{10}x+B \\ &\iff 10^{ \log_{10}y } = 10^{A\log_{10}x+B} \\ &\iff y = 10^B x^{A} \end{aligned}

となります。 $c =10^B$ と定めることで， $y=cx^A$ になり，確かにべき乗関数になりますね。

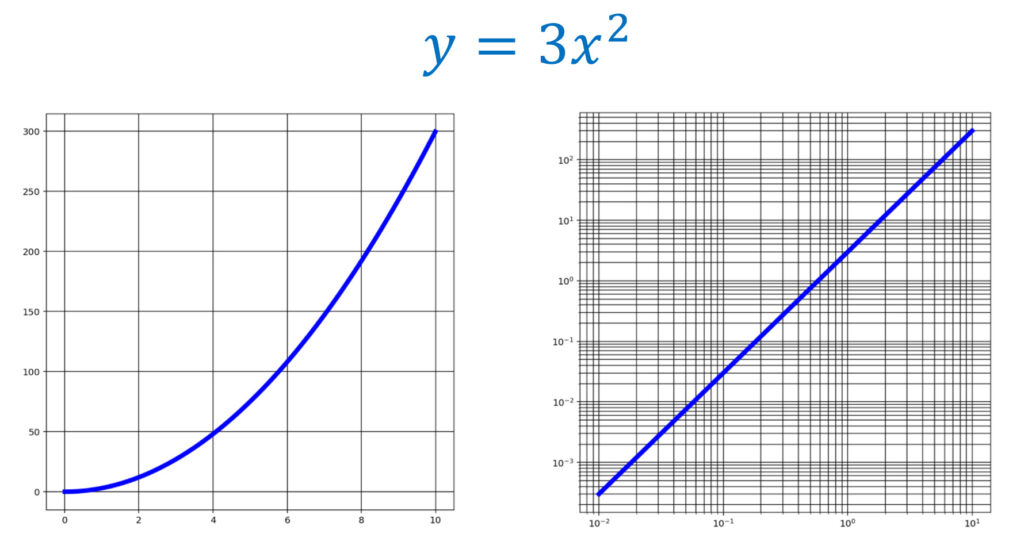
べき乗関数で近似したいものを両対数グラフで直線近似することで，べき乗関数で近似した際のパラメータ $A,c$ を求めることができるわけです。

以上を簡単にまとめておきましょう。

	片対数グラフ	両対数グラフ
特徴	片方の軸のみ $\log_{10}$ スケール	両方の軸が $\log_{10}$ スケール
直線になる曲線	$y= ce^{x}$ (指数関数)	$y=cx^a$ (べき乗関数)

対数グラフを使いこなしていきましょう。

以下のサイトで，自由な形式の対数グラフを作ることができます。