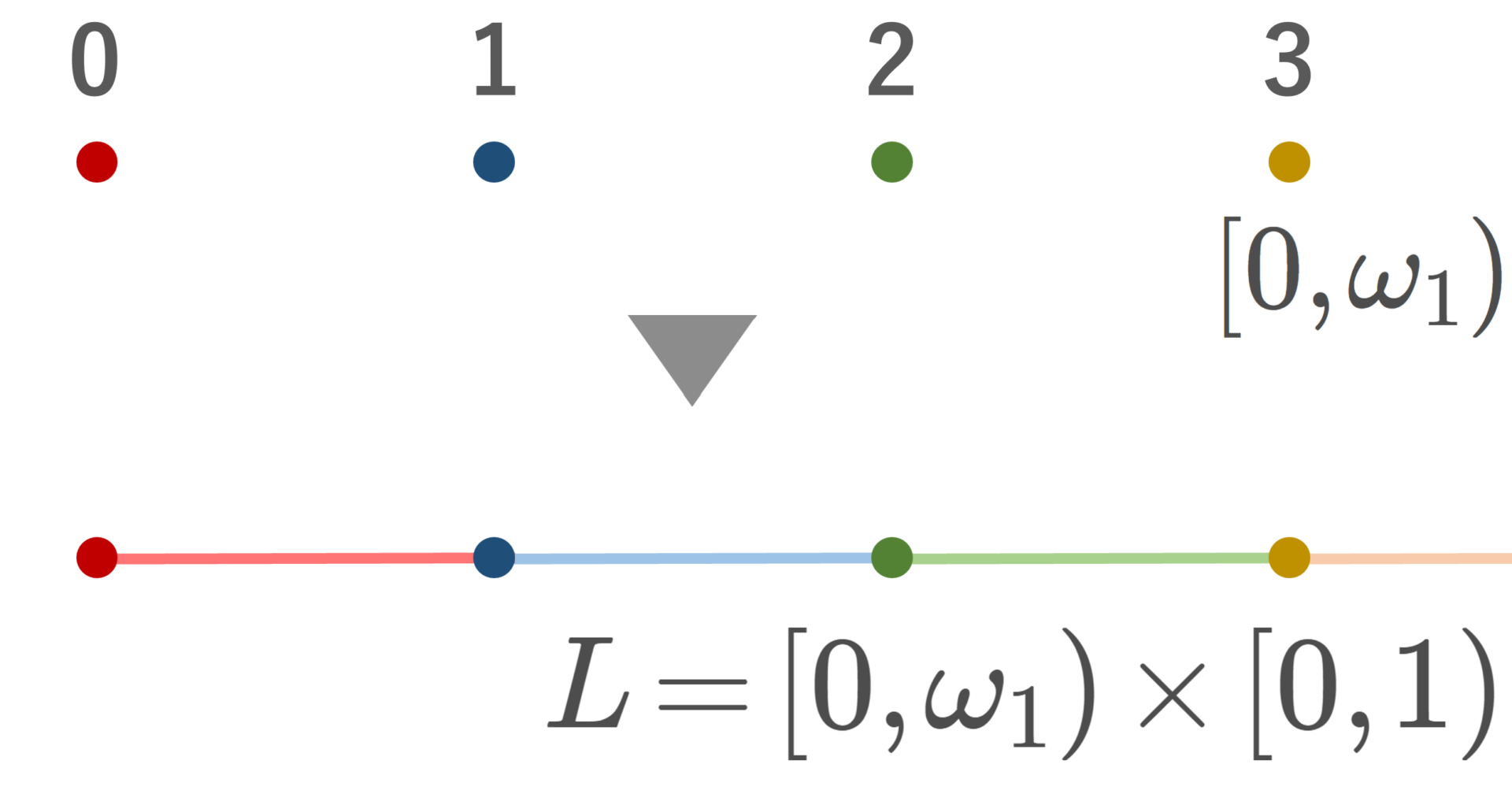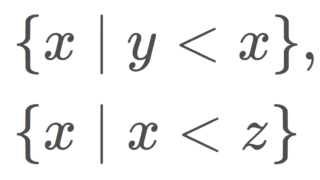長い直線とは,局所的には直線と同相ですが,直線よりはるかに長い直線で,順序数の間を連続的に埋める形で定義されます。
長い直線について,その位相的性質を調べましょう。順序数に関する知識はある程度既知とします。
長い直線(アレキサンドロフ直線)の定義
長い直線の理解には,順序数の知識が必要です。以下で確認しておきましょう。
本記事では, \omega_1 を最小の非可算順序数とし, \omega_1=[0,\omega_1)=\{0,1,2,\ldots\} とかき, \omega_1+1=[0,\omega_1]=\{0,1,2,\ldots, \omega_1\} とかきます。
定義(長い直線・アレキサンドロフ直線)
L= [0,\omega_1)\times [0,1) において,辞書式順序による順序位相を入れた位相空間を考える。これを長い直線 (long line) またはアレキサンドロフ直線 (Alexandroff line) という,
また, L に最大元を加えた L^* =L\cup \{\omega_1\} を拡張された長い直線 (extended long line) という。
今回, [0,\omega_1)\times [0,1) に入れる位相は直積位相ではなく,辞書式順序による順序位相です。 [0,\omega_1)=\{0,1,2,\ldots\} は局所的に離散的ですが,その間を [0,1) で埋めるイメージです。
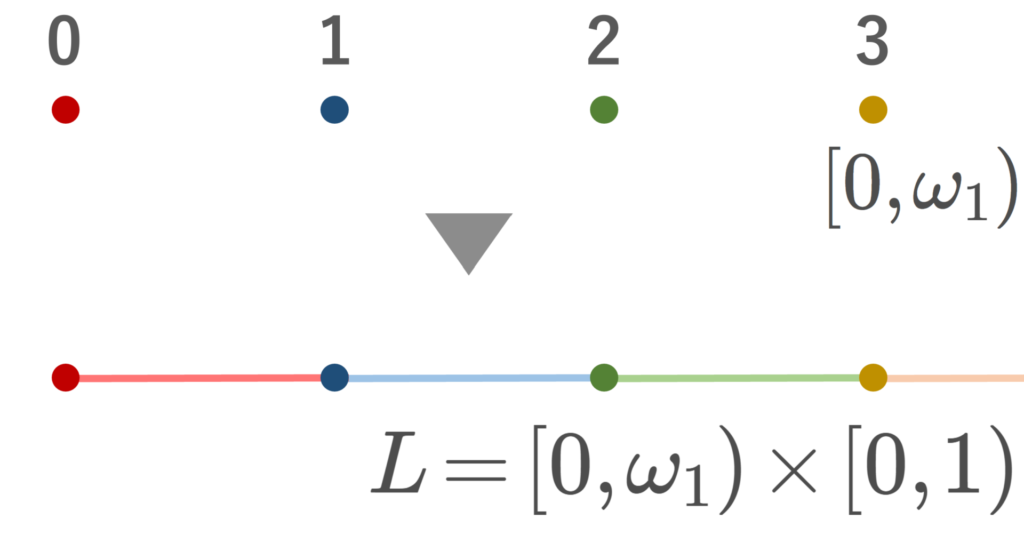
[0,\omega_1) が拡張された整数部分, [0,1) の方が小数部分のイメージです。
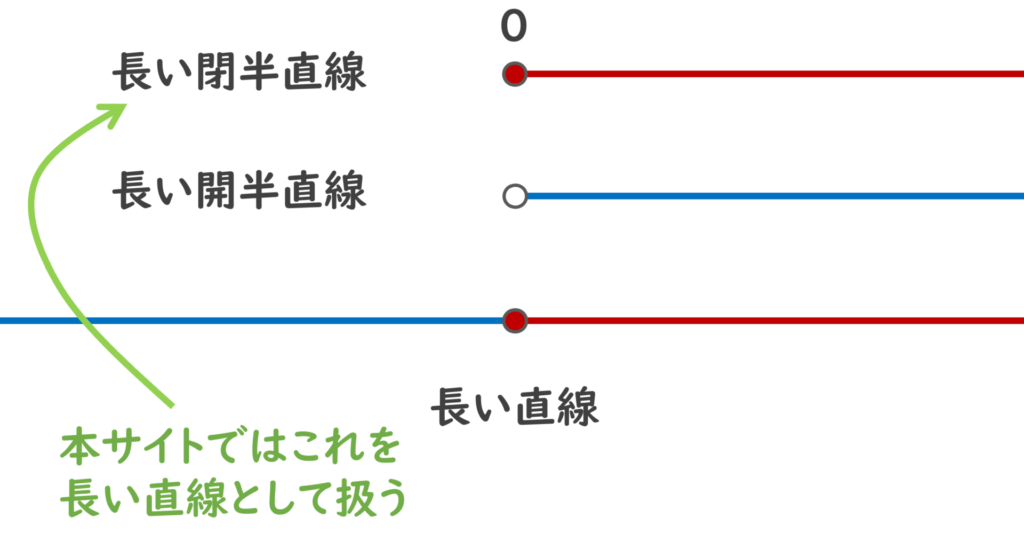
厳密には, L は長い閉半直線というべきかもしれません。また, L\setminus \{(0,0)\} を長い開半直線とし,長い閉半直線と長い開半直線を下のように逆方向につなげたものが,本来の意味の「長い直線」でしょう。しかし,本記事では文献[1]に合わせて,長い閉半直線を長い直線として扱います。
以下では,長い直線を「長い数直線」だと思って, x = (\alpha, r)\in [0,\omega_1)\times [0,1)=L は x=\alpha+r と考え,また x,y\in L に対し, x+y\in L みたいな表記も用います。
また,x,y\in L に対し, L における区間の表記も用います。たとえば, (x,y)=\{ r\in L\mid x<r<y\} です。この表記を用いれば, L=[0,\omega_1) や L^*=[0,\omega_1] ですが,順序数の集合として離散的な \omega_1=[0,\omega_1)=\{0,1,2,\ldots\} や \omega_1+1= [0,\omega_1]=\{0,1,2,\ldots, \omega_1\} とは異なり,間が詰まっている連続的なものです。文脈で判断してください。
\omega を最小の可算順序数とします。このとき,\omega=[0,\omega)\subset L は実数における部分集合 [0,\infty)\subset \R そのもの,すなわち通常の(閉半)直線とみることができます。 \omega_1 は,\omega よりはるかに大きいもの(集合)ですから,「長い直線」 L=[0,\omega_1) とは,通常の直線よりはるかに長い直線です。
長い直線(アレキサンドロフ直線)の性質
可算公理・分離公理・コンパクト性・連結性の順に解説しましょう。
長い直線と可算公理
L が第一可算であること以外は,順序数 \omega_1=[0,\omega_1)=\{0,1,2,\ldots\}, \,\omega_1+1=[0,\omega_1]=\{0,1,2,\ldots, \omega_1\} の可算公理の証明とほぼ同様に従うので,順序位相の定義と順序数における順序位相の性質をみてください。
L が第一可算である証明
x\in L\setminus\{0\} とする。このとき,( x が極限順序数であろうと, x-\varepsilon を考えることができる場合であろうと,どちらの場合であっても)狭義単調増加点列 (x_n)\subset L で,x_1<x_2<\cdots< x_n<\cdots \to x となるものが取れる。このときの \{ (x_n, x+1/n)\} は, x の可算な基本近傍系である。また,0\in L のまわりも基本近傍系 \{ [0, 1/n)\} が取れるので同じ。
証明終
長い直線と分離公理
| T_0,T_1, T_2, T_3, T_4, T_5 空間 | |
|---|---|
| L | 〇 |
| L^* | 〇 |
一般に,全順序集合における順序位相は,上の全ての分離公理をみたすことが知られています。証明は省略します。
長い直線とコンパクト性
証明については,順序数 [0,\omega_1)=\{0,1,2,\ldots\}, [0,\omega_1]=\{0,1,2,\ldots, \omega_1\} のコンパクト性の証明とほぼ同様です。順序位相の定義と順序数における順序位相の性質をみてください。
長い直線と連結性
| 連結・局所連結 | 弧状連結・弧連結 局所弧状連結・局所弧連結 | |
|---|---|---|
| L | 〇 | 〇 |
| L^* | 〇 | × |
定義は以下の通りです。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な空でない開集合 U,V で, U\cup V=X となっているものは存在しない |
| 局所連結 (locally connected) | 各点で連結な基本近傍系をもつ |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について,ある連続写像 f\colon [0,1]\to X で, f(0)=x, f(1)=y となるものが存在する |
| 局所弧状連結 (locally path connected) | 各点で弧状連結な基本近傍系をもつ |
| 弧連結 (arc connected) | 上の f として,埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる(※単に全単射なものが取れるとすることもある。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値) |
| 局所弧連結 (locally arc connected) | 各点で弧連結な基本近傍系をもつ |
順序数 [0,\omega_1)=\{0,1,2,\ldots\}, [0,\omega_1]=\{0,1,2,\ldots, \omega_1\} は「飛び飛びの数」なので完全不連結ですが,「間を埋めた」 L や L^* では性質が異なります。証明しましょう。
最初の方に定義しましたが,\omega は最小の可算順序数です。
証明
L について
弧連結であることを示せれば,弧状連結・連結は自動的に従うので,弧連結を示す。
まず,正の整数 n\ge 1 に対し, [0, n\omega]\cong\! [0,1] (\cong\! は同相(位相同型)の意味) を示す。これは例えば f\colon [0,n\omega]\to [0,1] を
f(x)=\begin{dcases}\frac{k+1-e^{k\omega-x}}{n} & k\omega\le x<(k+1)\omega, \\ 1& x=n\omega\end{dcases}
とすればよい。実際, [0,\omega]\stackrel{f_1}{\cong} \! [0,a_1],\, [\omega, 2\omega]\stackrel{f_2}{\cong}\! [a_1 , a_2],\ldots として, f_1(\omega)=f_2(\omega)=a_1, \, f_2(2\omega)=f_3(2\omega)=a_2,\ldots となるものが構成できれば良い(繋ぎ合わせ)。
x,y\in L を x<y とする。区間 [x,y]\subset L に含まれている極限順序数の個数は高々可算個である。有限個のときは,前半の証明と同様である。可算個のときを考える。
簡単のため, x,y も極限順序数とする(そうでなくても x と, x 以上の最小の極限順序数までとを繋ぎ合わせ,同様に y 側の端も繋ぎ合わせればよい)。 [x,y] 間にある極限順序数を番号付けて,\Gamma_1, \Gamma_2, \ldots とする。番号付けは \Gamma_1<\Gamma_2<\cdots になるとは限らない(できないかもしれない)ことに注意する。このとき,極限順序数 \gamma\in \{\Gamma_1, \Gamma_2, \ldots\} に対し,
a_\gamma = \sum_{n;\, \Gamma_n < \gamma} \frac{1}{2^n}\in [0,1]
と定めると, \gamma\mapsto a_\gamma は順序を保つ写像である。ただし, \sum_{n;\, \Gamma_n < \gamma} は, {\Gamma_n < \gamma} をみたす n について和を取ることを指す(無限和のこともある)。このとき,極限順序数 \gamma, \gamma' に対し,L\supset [\gamma, \gamma']\cong\! [a_{\gamma_1}, a_{\gamma'}]\subset [0,1] とできる。その繋ぎ合わせによって, [x,y]\cong\! [0,1] がわかる。
局所弧連結も同じ。
L^* について
もし, [0,\omega_1]\cong\! [0,1] とすると, [0,1] は,互いに素な閉区間の非可算個の和集合を部分集合に含まなければならないが, [0,1] における各閉部分区間には有理数が必ず含まれており,有理数は可算集合なので矛盾している。よって, L^* は弧連結でない。同様に \omega_1 の近傍は弧連結でないので,局所弧連結でもない。
L^* はハウスドルフ空間( T_2 空間)であり,ハウスドルフ空間では弧状連結と弧連結は同値であるから,L^* は弧状連結でもない。局所弧状連結でもない。
一方で, L\subset L^* は弧連結なので連結である。 \overline{L}=L^* であることと,連結集合の閉包は連結なので,L^* も連結である。同様に局所連結でもある。
証明終