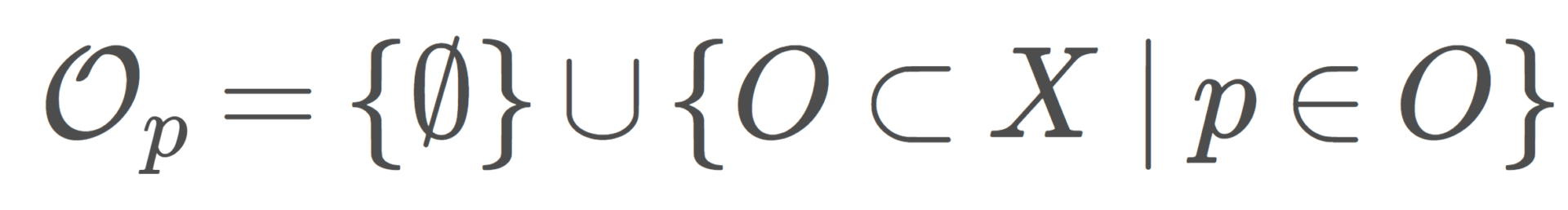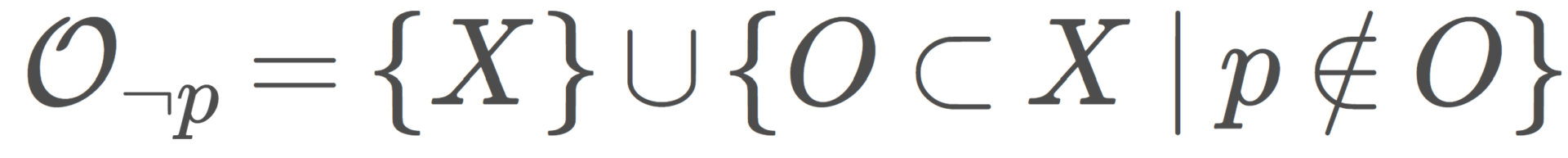特定点位相の定義と性質について詳しく

特定点位相とは，ある特定の点 $p$ を含む部分集合全体を開集合系にするような位相空間で，連結性はもちますが，コンパクトとは言えない空間です。

また，可分ですが部分空間が可分でない例や，コンパクトですが相対コンパクトでないような例を作るのにも用いられます。

特定点位相の定義と性質を掘り下げましょう。

特定点位相の定義
特定点位相の性質
関連する記事
参考

特定点位相の定義

定義（特定点位相）

$X$ を空でない集合とし， $p\in X$ とする。

\Large \color{red}\mathcal{O}_p =\{\emptyset\}\cup \{ O\subset X\mid p\in O\}

を， $p$ を含む部分集合全体の集合（と空集合の和集合）とすると， $(X,\mathcal{O}_p)$ は位相空間となる。この位相を特定点位相 (particular point topology) という。

特定の点 $p$ を含む集合が開集合族になるので，特定点位相と呼ばれるんですね。

ここで， $X$ が1点集合であるときは，特に面白くないです。また， $X$ が2点集合のときは，シェルピンスキー空間 (Sierpinski space) と呼ばれます。シェルピンスキー空間は，【位相空間】シェルピンスキー空間の定義と性質でも解説しています。ここからは， $X$ が

2点集合（シェルピンスキー空間）
3点以上の有限集合
可算集合
非可算集合

に分けて，性質を解説しましょう。

特定点位相の性質

可算性・分離性・コンパクト性・連結性に分けて性質を解説しますが，最初に全てまとめておきます。

$X$ の濃度	2点 (シェルピンスキー空間)	3点以上の有限集合	可算集合	非可算集合
第一可算	〇	〇	〇	〇
第二可算	〇	〇	〇	×
可分	〇	〇	〇	〇部分空間 $X\setminus \{p\}$ は × (可分空間の部分空間が可分でない例)
$T_0$ 空間	〇	〇	〇	〇
$T_1, T_2, T_3$ 空間	×	×	×	×
$T_4, T_5$ 空間	〇	×	×	×
コンパクト	〇	〇	×	×
点列コンパクト	〇	〇	×	×
局所コンパクト (各点がコンパクトな近傍をもつ)	〇	〇	〇	〇
強局所コンパクト (各点がコンパクトな閉近傍をもつ)	〇	〇	×	× $\{p\}$ はコンパクトだが相対コンパクトでない例(可算集合でも同じ)
連結	〇	〇	〇	〇
弧状連結	〇	〇	〇	〇
弧連結	×	×	×	×
hyperconnected	〇	〇	〇	〇
ultraconnected	〇	×	×	×

順番に考えます。

1. 特定点位相と可算公理

定理1（特定点位相と可算公理）

$(X,\mathcal{O}_p)$ を特定点位相が入った位相空間とする。このとき，

$X$ は第一可算である。
$X$ が高々可算集合であるとき第二可算であり，非可算集合のときは第二可算でない。
$X$ は可分である。

定理1の証明

1.について，各点 $x\in X\setminus \{p\}$ に対し， $\mathcal{B}_x = \bigl\{\{x, p\}\bigr\}$ は $x$ の基本近傍系である。また， $\mathcal{B}_p=\bigl\{\{ p\}\bigr\}$ は $p$ の基本近傍系である。よって， $X$ は第一可算である。

2.について，

\mathcal{B}=\bigl\{\{p\}\bigr\} \cup\bigl\{ \{x, p\}\mid x\in X\setminus \{p\}\bigr\}

とすると，これは $(X,\mathcal{O}_p)$ の開基であり，逆に全ての開基は $\mathcal{B}$ を含む。よって， $X$ が高々可算なら第二可算であるし，非可算なら第二可算でない。

3.について， $\overline{\{p\}}=X$ であるから，可分である。

証明終

補足ですが， $X$ は可分である一方，その部分空間 $X\setminus\{p\}$ は離散位相空間のため， $X$ が非可算なら可分ではありません。これは，可分である空間の部分空間が必ずしも可分でないことの例になっています。

2. 特定点位相と分離公理

定理2（特定点位相と分離公理）

$X$ を2点以上の集合とし， $(X,\mathcal{O}_p)$ を特定点位相が入った位相空間とする。このとき，

$X$ は $T_0$ 空間である。
$X$ は $T_1, T_2, T_3$ 空間でない。
$X$ が2点集合(シェルピンスキー空間)のとき， $T_4, T_5$ 空間であるが，そうでないときは， $T_4. T_5$ 空間でない。

本記事では， $T_0$ から $T_5$ は以下のように定義しています。この定義は文献によって変わりますから，注意してください。

名称	定義
$T_0$ コルモゴロフ空間 (Kolmogorov space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ または $x\notin O_y,\, y\in O_y$ となる開集合 $O_y$ の少なくとも一方が取れる
$T_1$	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ と $x\notin O_y, \,y\in O_y$ となる開集合 $O_y$ の両方が取れる
$T_2$ ハウスドルフ空間 (Hausdorff space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset$ となる開集合 $O_x, O_y$ が取れる
$T_3$	任意の閉集合 $F$ と任意の点 $x\in X\setminus F$ に対して， $F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset$ となる開集合 $O_F, O_x$ が取れる
$T_4$	任意の2つの互いに素な空でない閉集合 $F,G\subset X$ に対して， $F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset$ となる開集合 $O_F, O_G$ が取れる
$T_5$	$\overline{A}\cap B=A\cap \overline{B}=\emptyset$ をみたす任意の2つの空でない集合 $A,B\subset X$ に対して， $A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset$ となる開集合 $O_A, O_B$ が取れる

定理2の証明

1.について， $x, y\in X$ を異なる2点とする。どちらも $p$ でないとすると， $\{x, p\}$ は $x$ は含むが $y$ は含まない開集合である。また， $x=p$ なら， $\{p\}$ が $x=p$ を含むが $y$ を含まない開集合なので， $T_0$ 分離公理をみたす。

2.について， $x\in X\setminus \{p\}$ とする。空でない開集合は常に $p$ を含むので， $x$ を含むが $p$ を含まない開集合は存在しない。よって， $T_1,T_2$ でない。 $\{x\}$ は閉集合なので，同様に $T_3$ でもない。

3.について， $X$ が2点集合のときは，そもそも上記 $T_4$ の定義をみたすような $F,G$ や， $T_5$ の定義をみたすような $A,B$ が取れない。よって， $T_4, T_5$ であるといえる(空虚な真)。

$X$ が 3点以上の集合のときは， $x, y\in X\setminus \{p\}$ を異なる2点とすると， $\{x\}, \{y\}$ は閉集合であり， $\{x\}\subset O_x, \, \{y\}\subset O_y$ となる開集合 $O_x, O_y$ は $p\in O_x\cap O_y$ となってしまい，右辺は空集合にならないので， $T_4, T_5$ でない。

証明終

3. 特定点位相とコンパクト性

定理3（特定点位相とコンパクト性）

$X$ を2点以上の集合とし， $(X,\mathcal{O}_p)$ を特定点位相が入った位相空間とする。このとき，

$X$ が有限集合のときはコンパクトであるが，無限集合のときはコンパクトでない。
$X$ が有限集合のときは点列コンパクト(点列が常に収束部分列を持つ)であるが，無限集合のときは点列コンパクトでない。
$X$ は局所コンパクト(各点がコンパクトな近傍をもつ)である。
$X$ が有限集合のときは，強局所コンパクト(各点がコンパクトな閉近傍をもつ)であるが，無限集合のときは強局所コンパクトでない。

定理3の証明

1.について，有限集合がコンパクトであることは明らか。 $X$ が無限集合のときは，

\mathcal{C}=\bigl\{\{ x, p\}\mid x\in X\bigr\}

は開被覆であるが，有限部分被覆が存在しないので，コンパクトでない。

2.について，有限集合が点列コンパクトであることは明らか。 $X$ が無限集合のときは， $\{x_n\}\subset X$ を，任意の2点が異なる点列とすると，これは収束しないので点列コンパクトでない。

3.について， $x\in X$ に対し， $\{x, p\}$ は $X$ のコンパクトな開近傍なので，局所コンパクトである( $x=p$ のときは， $\{x, p\}=\{p\}$ と考える)。

4.について， $x\in X$ に対し， $x$ の任意の近傍は $p$ を含む。 $p$ を含む閉集合は $X$ しかないので， $x$ の閉近傍は $X$ しかない。1.より， $X$ が有限集合のときは強局所コンパクトで，無限集合のときはそうではない。

証明終

$\{p\}$ は1点集合なのでコンパクトですが，その閉集合 $\overline{\{p\}}=X$ は， $X$ が無限集合のときはコンパクトではありません。 $\{p\}$ は，コンパクトだが相対コンパクトでないものの例になっています。

4. 特定点位相と連結性

定理4（特定点位相と連結性）

$X$ を2点以上の集合とし， $(X,\mathcal{O}_p)$ を特定点位相が入った位相空間とする。このとき，

$X$ は連結である。
$X$ は弧状連結である。
$X$ は弧連結でない。
$X$ は hyperconnected である。
$X$ は2点集合(シェルピンスキー空間)のとき，ultraconnected であり，3点以上の集合のときは ultraconnected でない。

まず定義を確認しておきましょう。

名称	定義
連結 (connected)	2つの互いに素な開集合 $U,V$ で， $U\cup V=X$ となっているものは存在しない
弧状連結 (path connected)	任意の異なる2点 $x,y\in X$ について，ある連続写像 $f\colon [0,1]\to X$ で， $f(0)=x, f(1)=y$ となるものが存在する
弧連結 (arc connected)	上の $f$ として，埋め込みすなわち $f\colon [0,1]\to f([0,1])$ が同相となっているものが常に取れる（※単に全単射なものが取れるとすることもある。 $X$ がハウスドルフ ( $T_2$ )なら弧状連結と弧連結は同値）
hyperconnected	任意の空でない2つの開集合が常に共通部分を持つ
ultraconnected	任意の空でない2つの閉集合が常に共通部分を持つ

定義から，4,5.はほぼ明らかで，これより，1.も言えます。2.と3.のみ示しましょう。

定理4の証明

2.について， $x\in X\setminus \{p\}$ に対し，

f(t)=\begin{cases} p & 0\le t<1, \\ x & t=1\end{cases}

とすると， $f$ は連続である。また，異なる2点 $x,y\in X\setminus \{p\}$ に対し，

g(t)=\begin{cases} x & t=0, \\ p& 0<t<1,\\ y& t=1\end{cases}

とすると， $g$ は連続である。よって，弧状連結である。

3.について， $X$ が高々可算集合のときは，全単射 $f\colon [0,1]\to X$ が存在しないので，弧連結でない。

$X$ が非可算集合とする。全単射かつ連続な $f\colon [0,1]\to X$ が存在したとすると， $[0,1]$ はコンパクトより， $f([0,1])$ はコンパクトである。定理3.1より， $f([0,1])$ は有限集合になるが， $f$ が全単射であることに矛盾する。したがって， $X$ は弧連結でない。