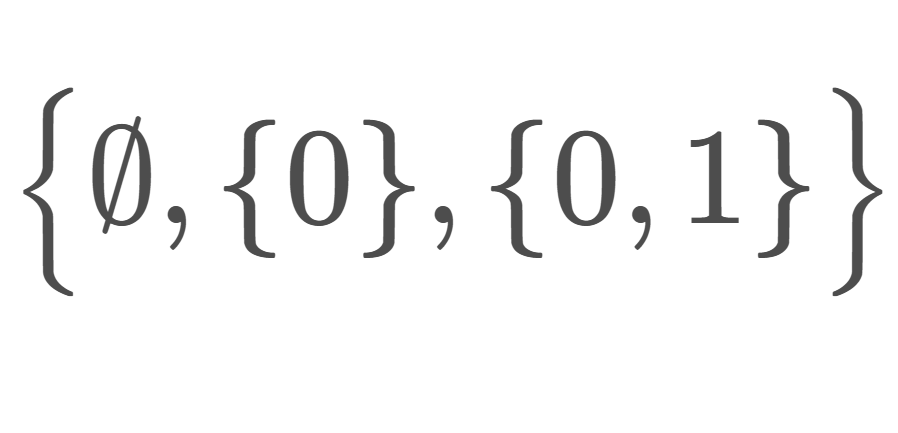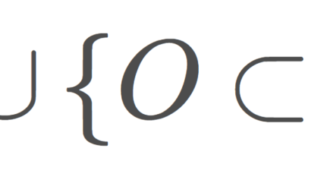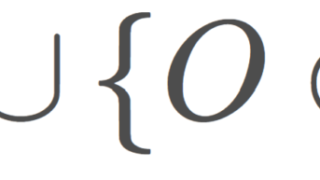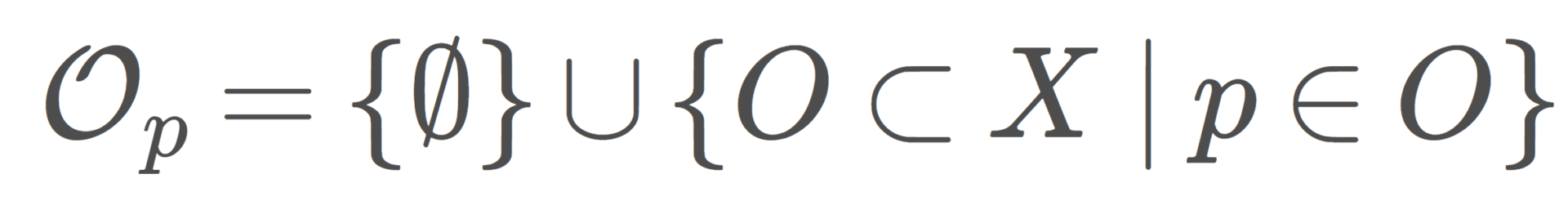シェルピンスキー空間とは，2点集合 \{0,1\} に，密着位相でも離散位相でもない開集合族 \bigl\{ \emptyset, \{0\}, \{0,1\}\bigr\} を入れた位相空間で，非常に基本的な位相空間の一つです。
シェルピンスキー空間は， T_0 空間であるが， T_1 空間でない例としても登場します。シェルピンスキー空間の定義・性質について紹介しましょう。
シェルピンスキー空間の定義
定義（シェルピンスキー空間）
2点集合 S=\{0,1\} について，その上の開集合族を
\color{red} \Large \mathcal{O}=\Bigl\{ \emptyset, \{0\}, \{0,1\}\Bigr\}
としたときの位相空間 (S,\mathcal{O}) をシェルピンスキー空間 (Sierpinski space) という。
シェルピンスキー空間は，2点集合に入る密着位相でも離散位相でもない位相です。開集合の補集合が閉集合なので，シェルピンスキー空間の閉集合族は
\large \mathcal{F}=\Bigl\{ \emptyset, \{1\}, \{0,1\}\Bigr\}
となります。開集合族が \mathcal{O}'=\bigl\{ \emptyset, \{1\}, \{0,1\}\bigr\} で，閉集合族が \mathcal{F}'=\bigl\{ \emptyset, \{0\}, \{0,1\}\bigr\} とすることもありますが，同じことです。
シェルピンスキー空間の性質
- 可算公理
- 分離公理
- コンパクト性
- 連結性
の順に性質を確認しましょう。
1. 可算公理
これは，そもそもシェルピンスキー空間 S=\{0,1\} が有限集合であることから直ちに従います。
2. 分離公理
定理2（シェルピンスキー空間と分離公理）
シェルピンスキー空間 (S,\mathcal{O}) は，
- T_0 空間である。
- T_1, T_2, T_3 空間ではない。
- T_4, T_5 空間である。
本記事では， T_0 から T_5 は以下のように定義しています。この定義は文献によって変わりますから，注意してください。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ空間 (Kolmogorov space) | 任意の異なる2点 x,y\in X に対して， x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して， x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ空間 (Hausdorff space) | 任意の異なる2点 x,y\in X に対して， x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F に対して， F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| T_4 | 任意の2つの互いに素な空でない閉集合 F,G\subset X に対して， F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの空でない集合 A,B\subset X に対して， A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
定理2が正しいことは，全て定義から確認可能です。 T_4, T_5 空間である理由は，そもそも「任意の2つの互いに素な空でない閉集合 F,G\subset X」や，「 \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの空でない集合」を取れないからです(空虚な真)。
3. コンパクト性
有限集合なので，どちらも明らかです。点列には，無限個の 0 または無限個の 1 が出現するため，部分列で 0 値定数列か， 1 値定数列をもちます。
もし，ある点列において，無限個の 0 と無限個の 1 の両方が出現するとき，この点列は 1 に収束するが， 0 には収束しません。一方で， 0,1 の両方が集積点となります。面白いですね。
4. 連結性
定理4（シェルピンスキー空間と分離公理）
シェルピンスキー空間 (S,\mathcal{O}) は，
- 連結 (connected) である。
- 弧状連結 (path connected) である。
- 弧連結 (arc connected) ではない。
- hyperconnected かつ ultraconnected である。
定義を確認しておきましょう。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な開集合 U,V で， U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について，ある連続写像 f\colon [0,1]\to X で， f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として，埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる（※ 単に f として全単射なものが取れるとすることもある） |
| hyperconnected | 任意の空でない2つの開集合が常に共通部分を持つ |
| ultraconnected | 任意の空でない2つの閉集合が常に共通部分を持つ |
定理4の1.と4.は定義から明らかです。3.も全単射 f\colon [0,1]\to \{0,1\} は存在しないので明らかです。2.の弧状連結について確認しましょう。 f\colon [0,1]\to \{0,1\} を
f(t)=\begin{cases} 0 & 0\le t< 1,\\ 1 & t=1 \end{cases}
とすると，これは連続で， 0 と 1 のパスになっているため，弧状連結が示せました。
