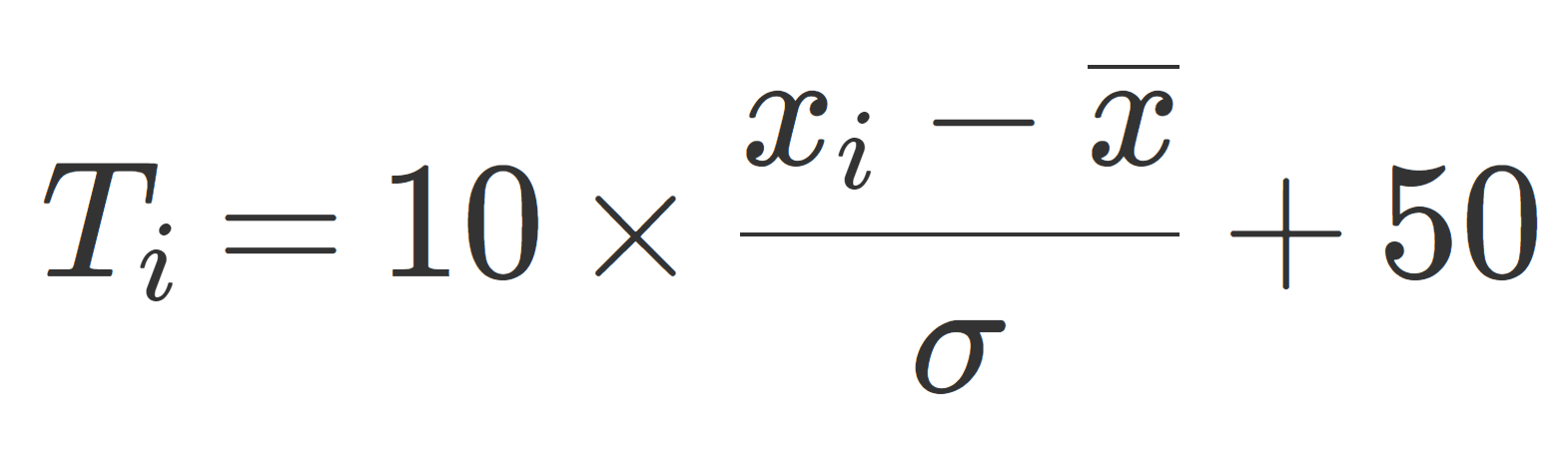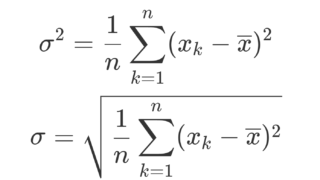よく,テストで点数と一緒に「偏差値」という数値が載っていることがあるでしょう。偏差値とは,母集団の相対的なランクを表すツールで,模試の成績によく用いられます。
偏差値について,その定義と,大体の数値の目安,偏差値のよくある勘違いを紹介します。
偏差値の定義
定義(偏差値)
データ x_1,x_2,\dots, x_n に対し,その平均値・標準偏差をそれぞれ \overline{x}, \sigma とする。このとき,
\Large \color{red} T_i=10\times\frac{ x_i-\overline{x}}{\sigma} +50
をデータ x_i に対する偏差値 (T-score) という。
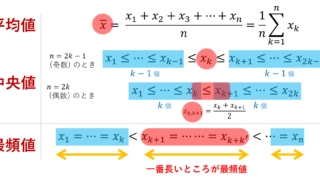
平均値 \overline{x}・標準偏差 \sigma の定義はそれぞれ
\begin{aligned}\overline{x}&=\frac{1}{n} \sum_{k=1}^n x_i ,\quad \sigma = \sqrt{\frac{1}{n}\sum_{k=1}^n (x_k-\overline{x})^2} \end{aligned}
です。
データが正規分布 N(\overline{x},\sigma^2) に従うと仮定しましょう。このとき,T_i=10\times\frac{ x_i-\overline{x}}{\sigma} +50 は平均 50,標準偏差 10 の正規分布 N(50,10^2) に従います。偏差値は,正規分布の標準化のような話だということです。
テストの点数データを考えるとき,一緒に偏差値を考えることが多いです。テストの点数は,テストの難易度によって変動がありますが,偏差値はその母集団の相対的な位置を表すため,難易度による変動は受けにくいと考えられます。
偏差値と大体の位置
データ x_1,x_2,\dots, x_n が正規分布に従うと仮定しましょう。正規分布とは,以下のような釣り鐘型の分布のことです。
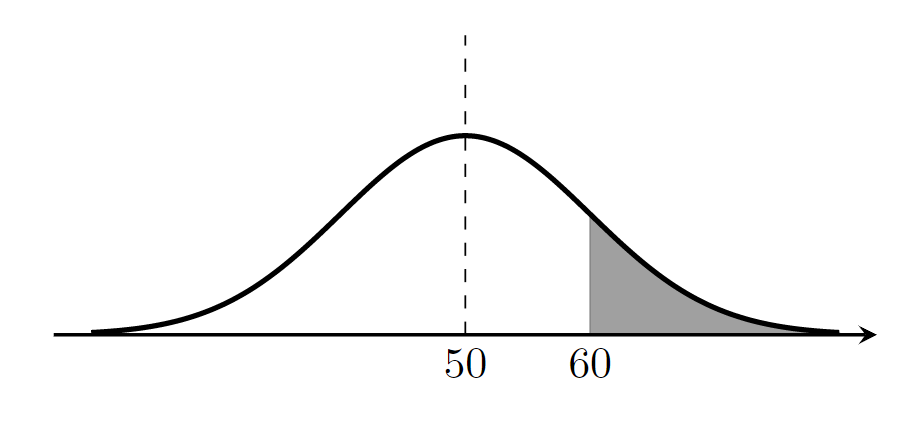
たとえば,偏差値60であれば,上の灰色の部分の面積は,全体の面積の15.866%を占めていることが分かります。よって,偏差値60は上位15.866%に入っているといえるわけです。
上位から何パーセントのところにいるかの大体の指標は以下の通りになります。たとえば,上位1%とは,100人に1人ということです。
| 偏差値 | 上位何%か | 偏差値 | 上位何%か |
|---|---|---|---|
| 100 | 0.0000287% | 50 | 50.000% |
| 99 | 0.0000479% | 49 | 53.983% |
| 98 | 0.0000793% | 48 | 57.926% |
| 97 | 0.000130% | 47 | 61.791% |
| 96 | 0.000211% | 46 | 65.542% |
| 95 | 0.000340% | 45 | 69.146% |
| 94 | 0.000541% | 44 | 72.575% |
| 93 | 0.000854% | 43 | 75.804% |
| 92 | 0.00133% | 42 | 78.814% |
| 91 | 0.00207% | 41 | 81.594% |
| 90 | 0.00317% | 40 | 84.134% |
| 89 | 0.00481% | 39 | 86.433% |
| 88 | 0.00723% | 38 | 88.493% |
| 87 | 0.0108% | 37 | 90.320% |
| 86 | 0.0160% | 36 | 91.924% |
| 85 | 0.0233% | 35 | 93.319% |
| 84 | 0.0337% | 34 | 94.520% |
| 83 | 0.0483% | 33 | 95.543% |
| 82 | 0.0687% | 32 | 96.407% |
| 81 | 0.0968% | 31 | 97.128% |
| 80 | 0.135% | 30 | 97.725% |
| 79 | 0.187% | 29 | 98.214% |
| 78 | 0.256% | 28 | 98.610% |
| 77 | 0.347% | 27 | 98.928% |
| 76 | 0.466% | 26 | 99.180% |
| 75 | 0.621% | 25 | 99.379% |
| 74 | 0.820% | 24 | 99.534% |
| 73 | 1.072% | 23 | 99.653% |
| 72 | 1.390% | 22 | 99.744% |
| 71 | 1.786% | 21 | 99.813% |
| 70 | 2.275% | 20 | 99.865% |
| 69 | 2.872% | 19 | 99.903% |
| 68 | 3.593% | 18 | 99.931% |
| 67 | 4.457% | 17 | 99.952% |
| 66 | 5.480% | 16 | 99.966% |
| 65 | 6.681% | 15 | 99.977% |
| 64 | 8.076% | 14 | 99.984% |
| 63 | 9.680% | 13 | 99.989% |
| 62 | 11.507% | 12 | 99.993% |
| 61 | 13.567% | 11 | 99.995% |
| 60 | 15.866% | 10 | 99.997% |
| 59 | 18.406% | 9 | 99.998% |
| 58 | 21.855% | 8 | 99.998665% |
| 57 | 24.196% | 7 | 99.999146% |
| 56 | 27.425% | 6 | 99.999549% |
| 55 | 30.854% | 5 | 99.999660% |
| 54 | 34.458% | 4 | 99.999789% |
| 53 | 38.209% | 3 | 99.999870% |
| 52 | 42.074% | 2 | 99.999921% |
| 51 | 46.017% | 1 | 99.999952% |
偏差値に関する注意事項
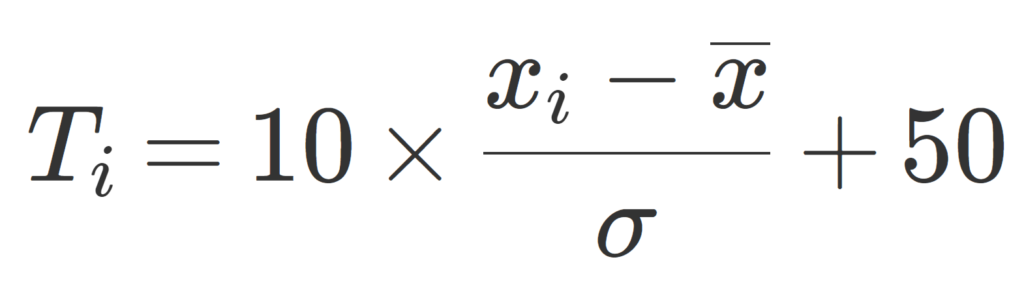
偏差値に関して,よく勘違いされることを解説しておきます。
偏差値が 50 だからと言って,ちょうど上位 50\% というわけではない。
定義の式より,偏差値 50 とは,平均と同じ値であるということです。一方で「上位 50\%」とは,中央値であることを指します。平均値と中央値は異なりますから,「偏差値 50 はちょうど真ん中」は間違えているわけです。
偏差値は負の値になったり, 100 を超えることもある。
偏差値は 50 がちょうど平均値になります。このことから,偏差値は 0 から 100 までの 100 点満点だと勘違いするかもしれません。というか,ミスリーディングな形をしていますね。しかし,偏差値は負の値になったり, 100 を超えることもあります。
たとえば,あるテストで 100 点が1人, 0 点が99人だったとしましょう。このとき, 0 点の人の偏差値は 49.0, 100 点の人の偏差値は \color{red}\boldsymbol{149.5} になります。
逆に, 100 点が99人, 0 点が1人だとすると, 100 点の人の偏差値は 51.0, 0 点の人の偏差値は \color{red}\boldsymbol{-49.5} になります。
本来偏差値は,このような正規分布に従わないようなものに適用すべきではありませんが,このようなことも起きるんですね。