位相空間論における T_1 空間,あるいはフレシェ空間であるとは, T_1-分離公理と呼ばれるものを満たす空間です。分離公理 (separation axioms) とは,各点が位相的にどのくらい「離れている」かを測る指標です。
T_1 空間について,その定義と具体例を T_0 空間(コルモゴロフ空間)や T_2 空間(ハウスドルフ空間)を織り交ぜながら,掘り下げましょう。
T1空間の定義と同値な性質
まず T_1 空間の定義を述べ,それから同値な性質を紹介しましょう。
T1空間の定義
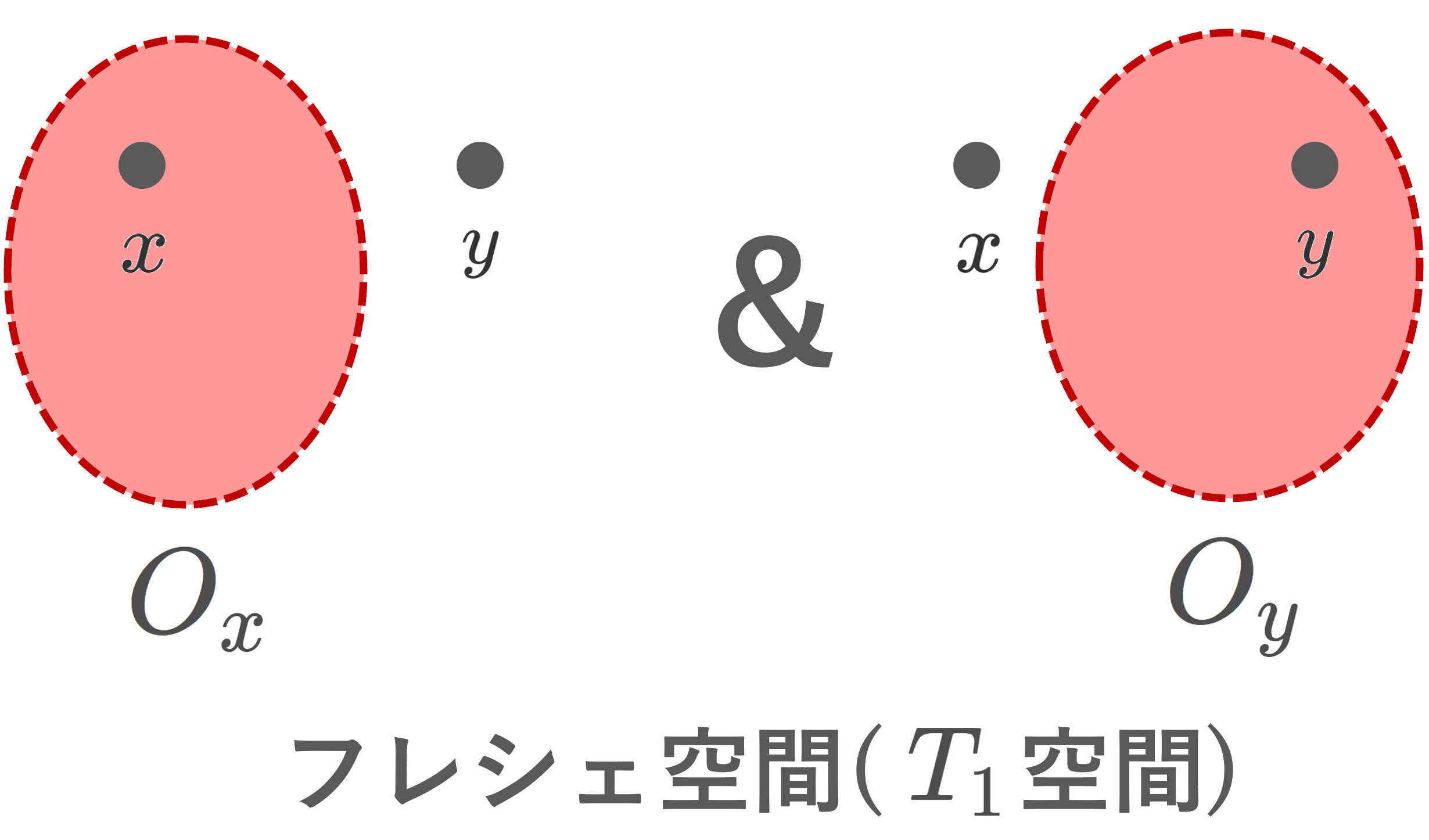
定義( T_1 空間(フレシェ空間))
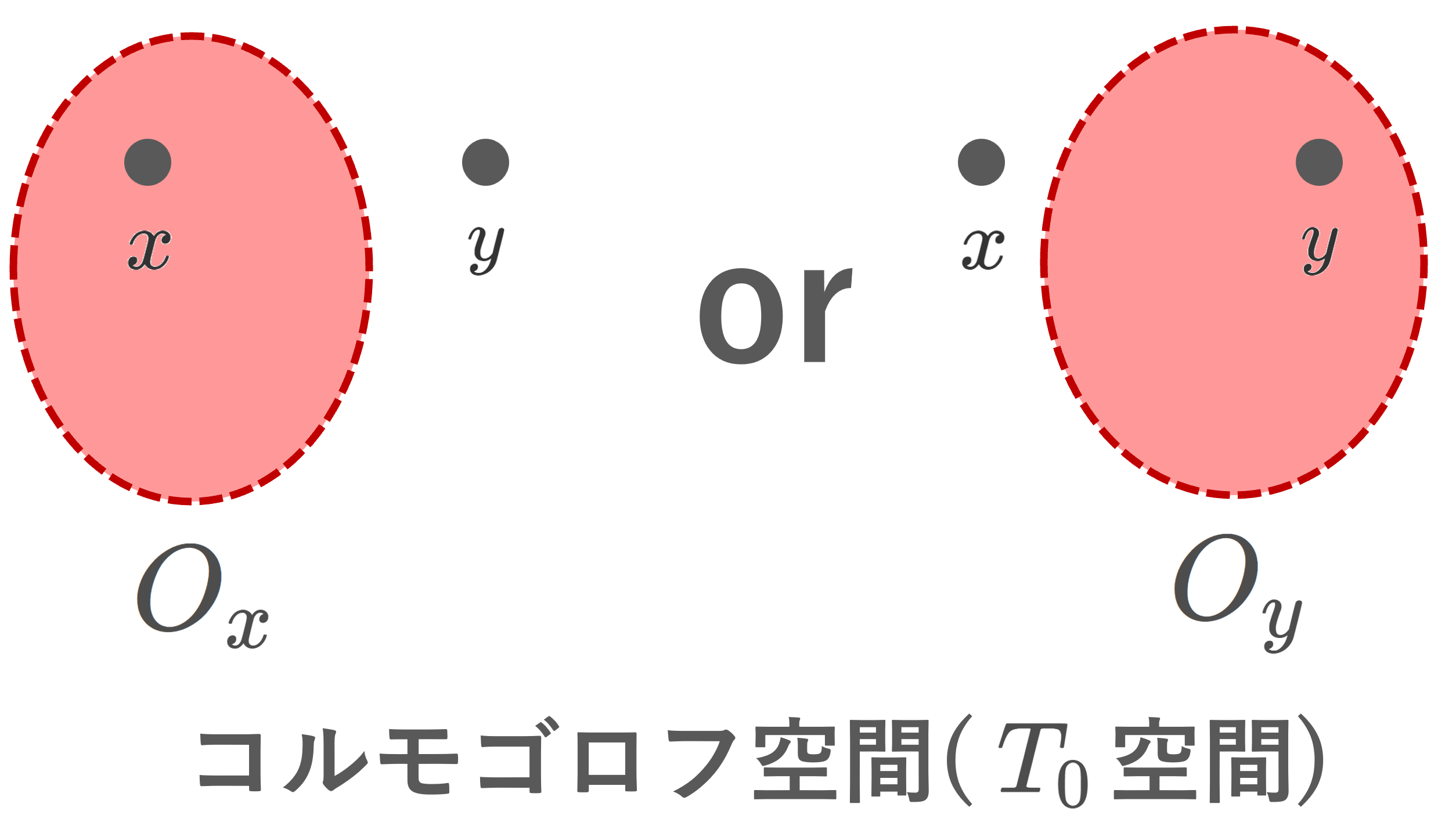
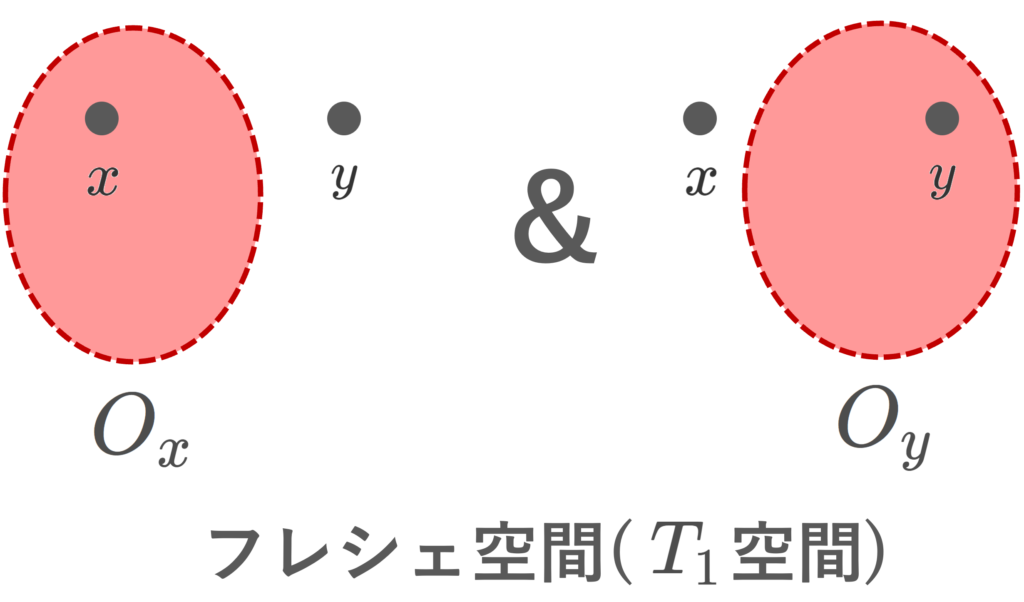
(X,\mathcal{O}) を位相空間とする。任意の異なる点 x, y\in X に対し,
x\in O_x かつ y \notin O_x となる O_x\in\mathcal{O}
x\notin O_y かつ y \in O_y となる O_y\in\mathcal{O}
の両方が存在するとき, (X,\mathcal{O}) は T_1 空間 ( T_1 space) またはフレシェ空間 (Fréchet space) であるという。
フレシェ空間という言い方は,関数解析学で別の意味で使うことがあるので, T_1 空間と言った方が勘違いがありません。
定義において,
x\in O_x かつ y \notin O_x となる O_x\in\mathcal{O}
x\notin O_y かつ y \in O_y となる O_y\in\mathcal{O}
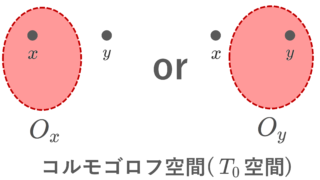
のうち,少なくとも一方が成立するような空間を T_0 空間 ( T_0 space) またはコルモゴロフ空間 (Kolmogorov space) といいます(→【位相空間】コルモゴロフ空間(T0空間)の定義と具体例)。

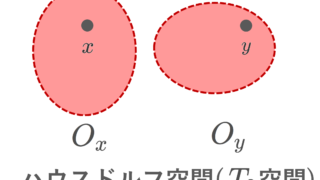
また, T_1 空間であって,かつ O_x\cap O_y=\emptyset とできるとき, T_2 空間 ( T_2 space) またはハウスドルフ空間 (Hausdorff space) といいます(→ハウスドルフ空間(T2空間)の定義・具体例・性質を詳しく)。
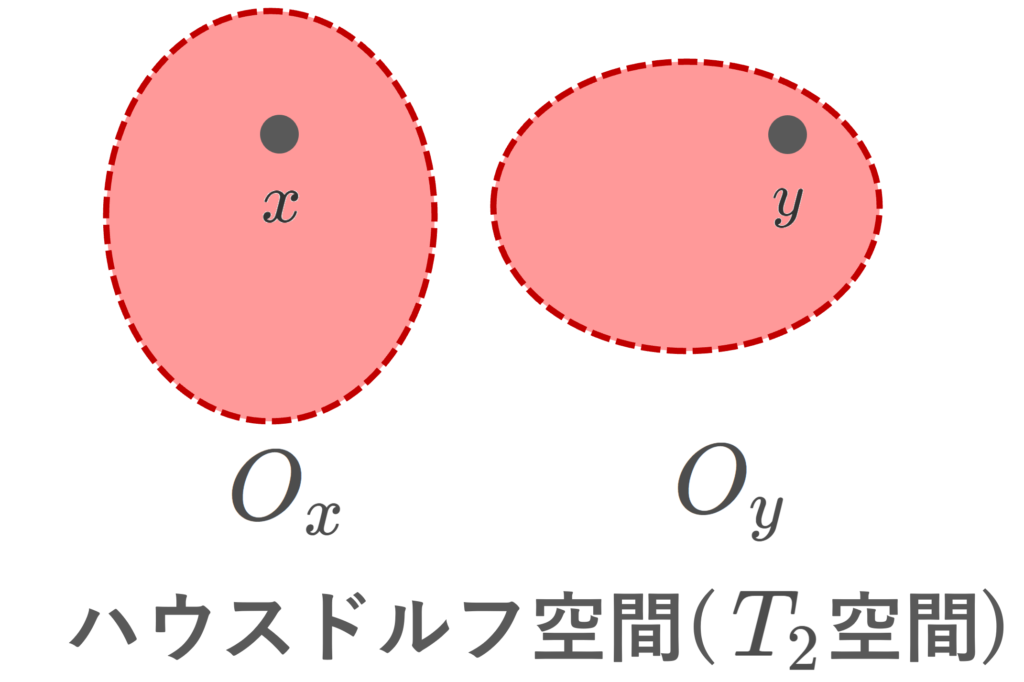
定義より明らかに T_2\implies T_1\implies T_0 です。
それ以外の分離公理もまとめておきます。定義は文献[1]に依っています。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ | 任意の異なる2点 x,y\in X が開集合で分離される, すなわち x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_{2 \frac {1}{2}} 完全ハウスドルフ | 任意の異なる2点 x,y\in X が閉近傍で分離される, すなわち x\in O_x, \, y\in O_y,\, \overline{O_x}\cap \overline{O_y}=\emptyset となる開集合 O_x, O_y が取れる |
| ウリゾーン | 任意の異なる2点 x,y\in X が連続関数で分離される, すなわち連続関数 f\colon X\to [0,1] で, f(x)=0,\, f(y)=1 となるものが取れる ※ ウリゾーンと T_{2\frac{1}{2}}(完全ハウスドルフ)の定義を逆にすることがある |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F が開集合で分離される, すなわち F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| 正則 (regular) | T_0 かつ T_3( \iff T_2 かつ T_3) ※ 正則と T_3 の定義を逆にすることがある |
| T_{3 \frac{1}{2}} 完全正則・チコノフ | 任意の閉集合 F と任意の点 x\in X\setminus F が連続関数で分離される, すなわち連続関数 f\colon X\to [0,1] で, f|_F=0,\, f(x)=1 となるものが取れる |
| T_4 | 任意の2つの互いに素な閉集合 F,G\subset X が開集合で分離される, すなわち F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| perfectly T_4 | T_4 かつ任意の閉集合が G_\delta 集合である |
| 正規 (normal) | T_1 かつ T_4( \iff T_2 かつ T_4\iff T_3 かつ T_4) ※ 正規と T_4 の定義を逆にすることがある |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの集合 A,B\subset X が開集合で分離される, すなわち A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
| completely 正規 | T_1 かつ T_5( \iff T_2 かつ T_5\iff T_3 かつ T_5) ※ completely 正規と T_5 の定義を逆にすることがある |
| T_6 perfectly 正規 | T_1 かつperfectly T_4 |
T1空間と同値な性質
T_1 空間であることと同値な性質を紹介しましょう。
定理1( T_1 空間と同値な性質)
(X,\mathcal{O}) を2点以上の点を持つ位相空間とするとき,以下は同値である。
これにより,たとえば2.を T_1 空間の定義にすることもあります。なお,2.より, T_1 かつ T_4 ならば T_3 も成立します。
1.\implies 2.\implies 3. \implies 4. \implies 1.の順に示します。
証明
1. \implies2.について
T_1 であることから, x\ne a に対し, x\notin O_a,\, a\in O_a となる開集合 O_a\in\mathcal{O} が存在する。
X\setminus \{x\}=\bigcup_{a\in X\setminus \{x\} }O_a
とかけるから, X\setminus \{x\} は開集合すなわち \{x\} は閉集合である。
2. \implies3.について
A\subset X に対し,
\bigcap_{b\in X\setminus A} (X\setminus \{b\}) =A
であり,2.より X\setminus \{b\} は A を含む開集合であるから,上式は A を含む開集合全体の共通部分集合を含む。すなわち
となるから,3.が示された。
3. \implies4.について
x\in X とする。3.で A=\{x\} とすると,
\bigcap_{x\in O\in\mathcal{O}} O=\{x\}
であり, x\in O\in\mathcal{O} をみたす O は O\in\mathcal{N}(x) となるので,
となるため,4.が示された。
4. \implies1.について
x,y\in X を異なる2点とする。3.より,ある N\in\mathcal{N}(x) が存在して, x\in N, \, y\notin N とできる。 N は x の近傍なので, x\in O\subset N となる開集合 O\in\mathcal{O} が取れて,この O は x\in O,\, y\notin O をみたす。
x と y の役割を入れ替えて同じ議論をすると, y\in O, \, x\notin O となる開集合 O\in\mathcal{O} の存在も言えるので, T_1 である。
証明終
T1空間の具体例とそうでない例
具体例を見ていきましょう。 T_0 空間(コルモゴロフ空間)や T_2 空間(ハウスドルフ空間)も絡めて見ていきます。
例1(密着空間・離散空間).
X を2元以上の集合とする。
(X, \{\emptyset, X\}) を密着空間とするとき,これは T_0 でも T_1 でも T_2 でもない。
(X, 2^X) を離散空間とするとき,これは T_0, T_1, T_2 である。
密着空間は開集合によって点が分離できず,離散空間は1点集合自身が開集合であるため,全ての点が開集合によって分離できます。
例2( \R).
実数の集合 \R に通常の位相を入れた空間はハウスドルフ空間( T_2 空間)であるため, T_1, T_0 でもある。
T_2\implies T_1\implies T_0 なので言えますね。
例3(距離空間).
距離空間はハウスドルフ空間( T_2 空間)であるため, T_1, T_0 でもある。
もっといろいろな例を挙げましょう。
例4.
X=\{a,b,c\},\,\mathcal{O}=\{\emptyset, \{a\}, \{a,b\} ,X \} とすると,(X,\mathcal{O}) は位相空間である。
この空間は, T_0 であるが T_1 ではない。
a と b は, a\in\{a\},\, b\notin \{a\} とできる, a と c は, a\in\{a\},\, c\notin \{a\} とできる, b と c は, b\in\{a,b\},\,c\notin \{a,b\} とできるので, T_0 です。
一方で, a\notin O,\, b\in O となる O\in \mathcal{O} はないので, T_1 ではありません。
例5(特定点位相).
X を2元以上の集合とし, x\in X とする。
\mathcal{O}=\{ O\subset X\mid x\in O\}\cup\{\emptyset\}
とすると, (X,\mathcal{O}) は位相空間である。この空間は T_0 であるが, T_1 ではない。
x を元に持つ集合全体(と \emptyset )を開集合族とする位相空間です。たとえば, x\ne a とすると, x\in \{x\},\,a\notin \{x\} だし, a\ne b をともに x と異なるとすると, a\in \{x,a\},\, b\notin \{x,a\} とできるので, T_0 です。
一方で, x\ne a に対し, x\notin O,\, a\in O となる O\in\mathcal{O} は存在しないので, T_1 ではありません。
特定点位相については,以下で掘り下げています。
例6(除外点位相).
X を2元以上の集合とし, x\in X とする。
\mathcal{O}=\{ O\subset X\mid x\notin O\}\cup\{X\}
とすると, (X,\mathcal{O}) は位相空間である。この空間は T_0 であるが, T_1 ではない。
さっきと逆で, x を元に持たない集合全体(と X)を開集合族とする位相空間です。 T_0 であることは確認してみてください。 x\ne a に対し, x\in O,\, a\notin O となる O\in\mathcal{O} は存在しないので, T_1 ではありません。
除外点位相は以下でも解説しています。
例7.
\mathcal{O}=\{ (0, x)\subset \R \mid 0<x\le 1\}\cup\{\emptyset\}
とすると, ((0,1), \mathcal{O}) は位相空間である。この空間は T_0 であるが, T_1 ではない。
0<x<y\le 1 に対し, x\in O,\, y\notin O となる O\in\mathcal{O} は存在しますが,逆に x\notin O,\, y\in O となる O\in\mathcal{O} は存在しませんね。
例8(補有限位相).
X を無限集合とし,
\mathcal{O}=\{ O\subset X\mid X\setminus O \text{ is finite}\}\cup\{\emptyset\}
を,補集合が有限集合である部分集合全体とすると, (X,\mathcal{O}) は位相空間である。この空間は T_1 であるが, T_2 ではない。
x,y\in X を,異なる2点とします。 X\setminus \{x\}, X\setminus \{y\} はどちらも開集合で,それぞれ x,y の一方を含み,もう一方を含まないので, T_1 の定義を満たしています。
一方で, T_2 と仮定すると,開集合 O_x, O_y\in\mathcal{O} を, x\in O_x,\, y\in \mathcal{O}_y,\, O_x\cap O_y=\emptyset となるように取れます。ここで, (X\setminus O_x)\cup(X\setminus O_y) = X ですから, X\setminus O_x,X\setminus O_y の少なくとも一方は無限集合になります。これは,補集合が有限集合であることに矛盾していますね。
補有限位相は,以下でも解説しています。
例9.
通常の位相が入った \R と,離散空間 \{ 0,1\} の積空間である,2つの数直線 \widehat{X}=\R\times \{0,1\} に対し,同値関係
(t, 0)\sim (t,1) \quad t<0
による商空間 X=\widehat{X}/\sim を考えると,この空間は T_1 であるが, T_2 ではない。
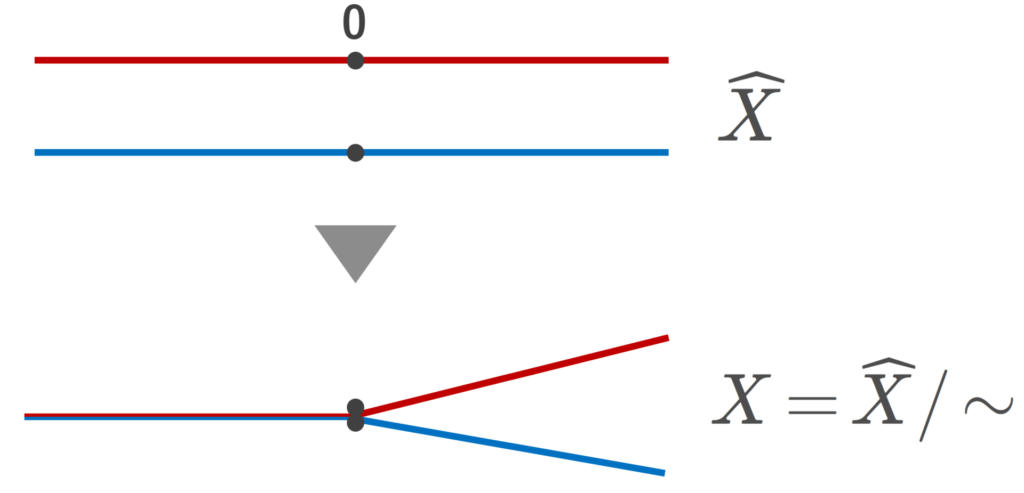
(0,0)\in X を含む開集合と (0,1)\in X を含む開集合は必ず共通部分を持ってしまうので, T_2 ではありません。
T1空間の性質
ある位相空間が T_0, T_1, T_2 なら,その部分空間も T_0, T_1, T_2 だし,直積空間もそうです。
定理2(分離公理と部分空間・直積)
1.については, T_2 の場合に,相対位相と部分位相空間の定義・具体例5つ・性質5つの中で証明しています。2.も T_2 の場合に直積位相とは~定義・具体例・性質~の中で証明しています。