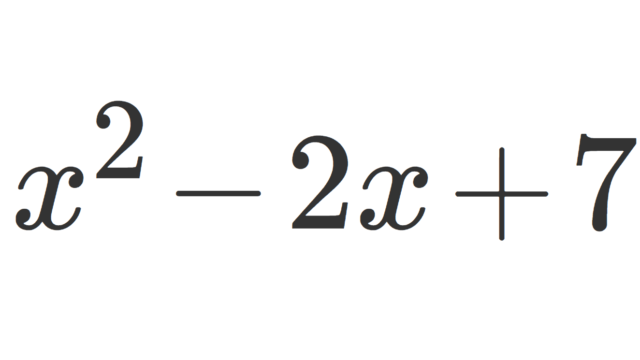 群・環・体
群・環・体 モニック多項式とは~定義・例・性質~
モニック多項式 (monic polynomial) とは,最高次係数が1である一変数多項式のことを言います。モニック多項式について,簡単に定義・例・性質を紹介しましょう。
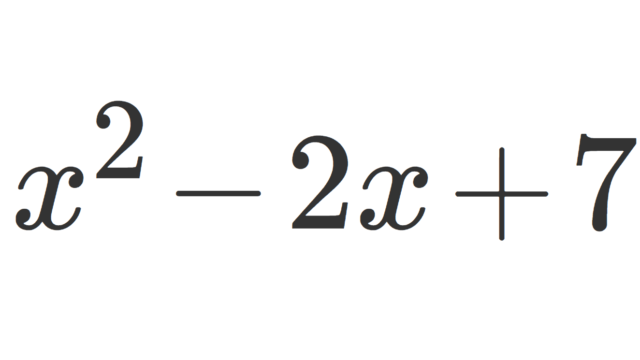 群・環・体
群・環・体  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他 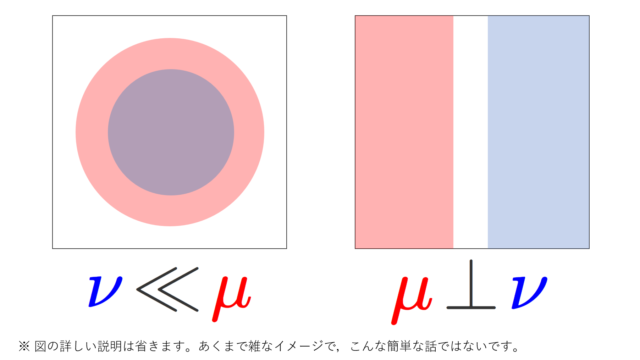 測度論
測度論 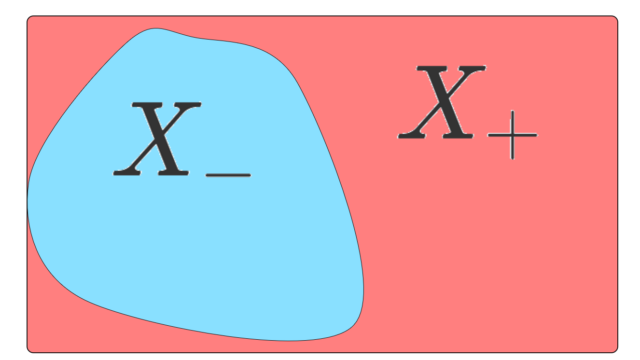 測度論
測度論 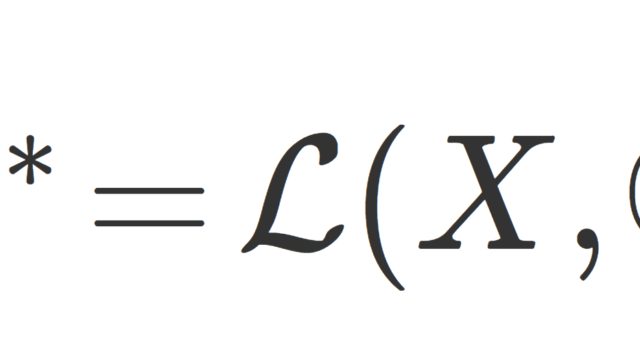 関数解析学
関数解析学 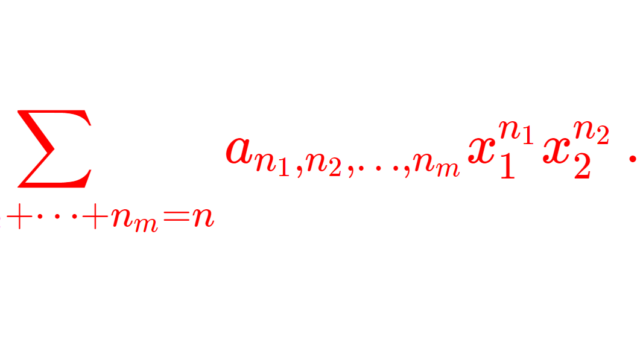 群・環・体
群・環・体 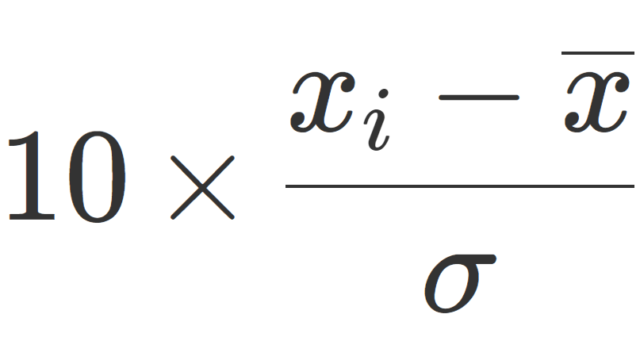 統計学
統計学 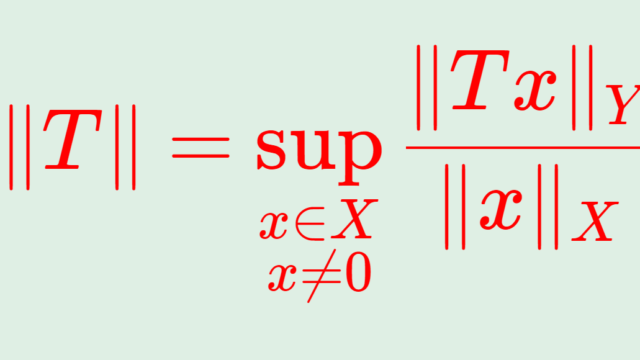 関数解析学
関数解析学 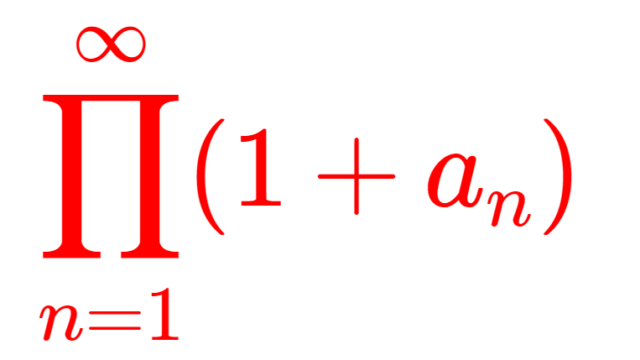 解析学(大学)その他
解析学(大学)その他