 集合と位相
集合と位相 ハウスドルフ空間(T2空間)の定義・具体例・性質を詳しく
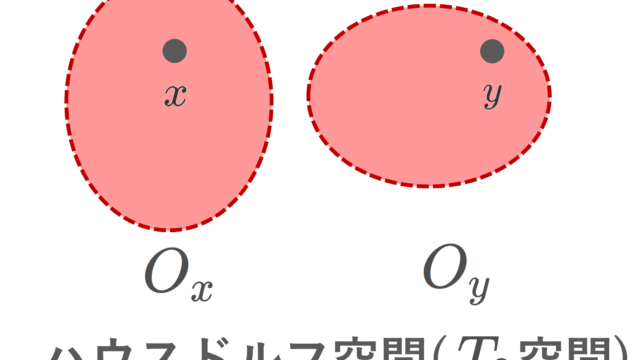
ハウスドルフ空間(T2空間)とは,任意の異なる2点が,開集合によって分離される空間のことをいいます。言い換えると,2点の開近傍で,共通部分をもたないものを取ってこれるということです。ハウスドルフ空間は,距離空間や位相多様体・関数解析における弱位相など,位相空間の応用上,最も成り立つ性質の一つと言えます。ハウスドルフ空間についての定義・具体例・性質を詳しく紹介しましょう。
 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 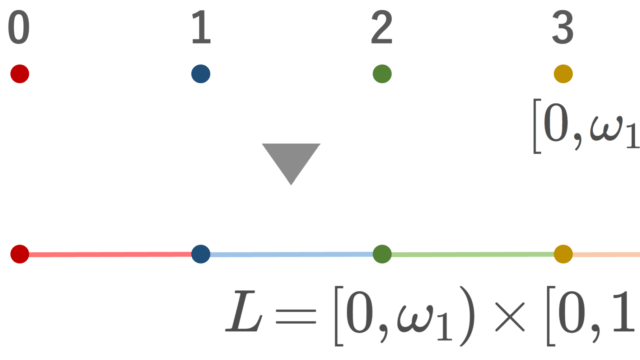 集合と位相
集合と位相 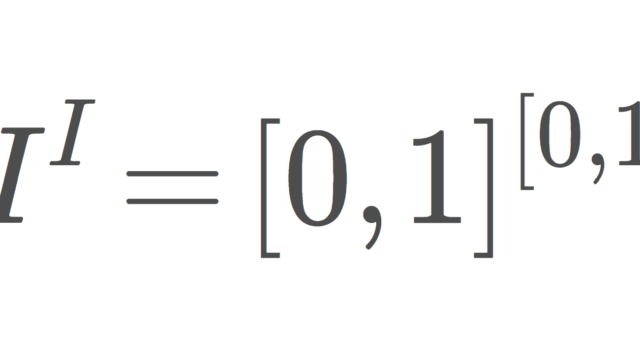 集合と位相
集合と位相 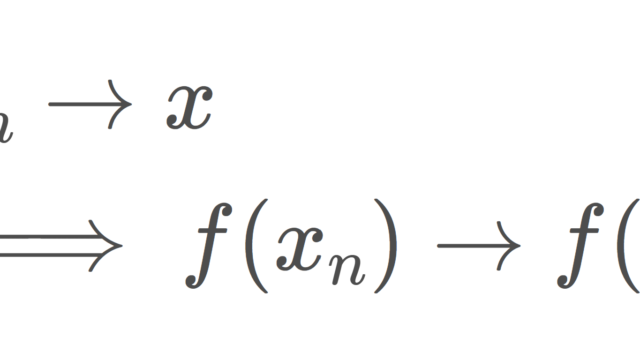 集合と位相
集合と位相