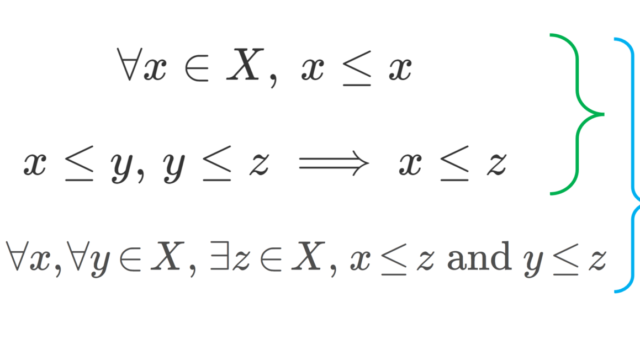 集合と位相
集合と位相 有向集合の定義と具体例6つ
有向集合とは,任意の2元に上界があるような前順序集合のことをいいます。位相空間におけるネット(有向点族)を定義する際の添え字としても用いられます。有向集合について,詳しく見ていきましょう。
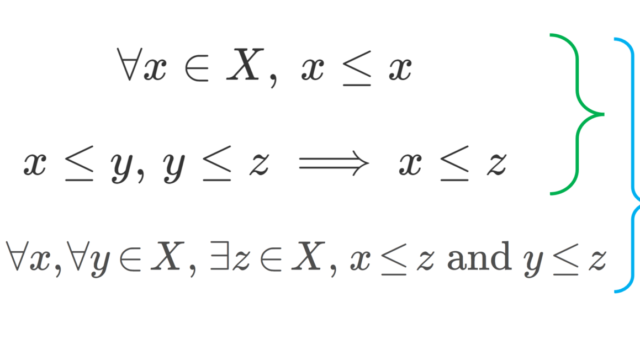 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 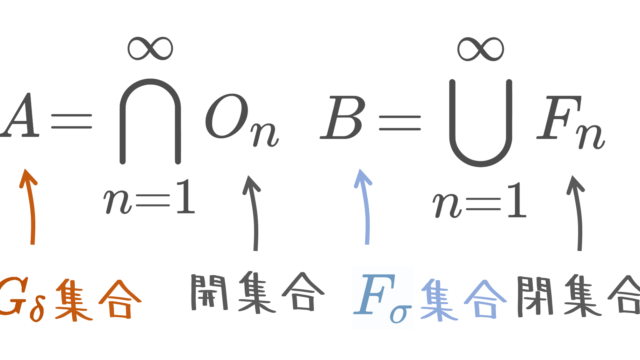 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 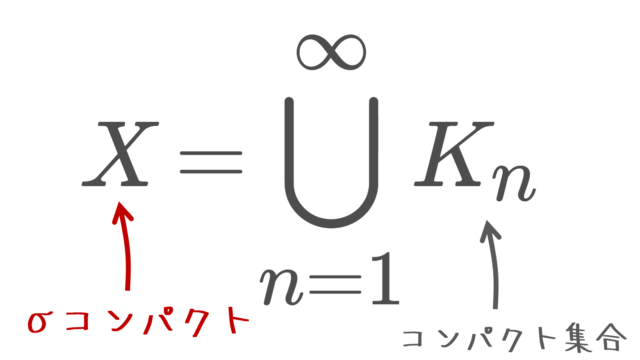 集合と位相
集合と位相