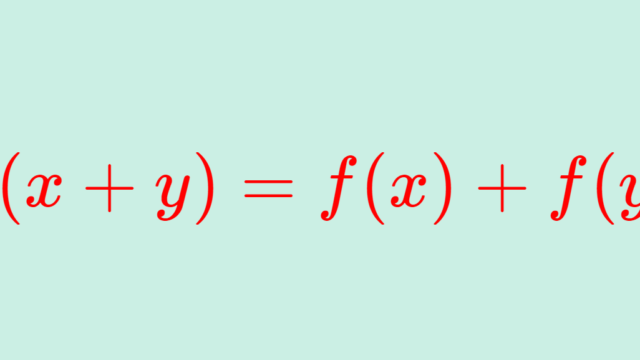 解析学(大学)その他
解析学(大学)その他 【f(x+y)=f(x)+f(y)】コーシーの関数方程式について詳しく
コーシーの関数方程式 (Cauchy's functional equation) とは,f(x+y)=f(x)+f(y)となる関数方程式のことを言います。これの解fを求め,さらにその関連である関数方程式の解を求めましょう。
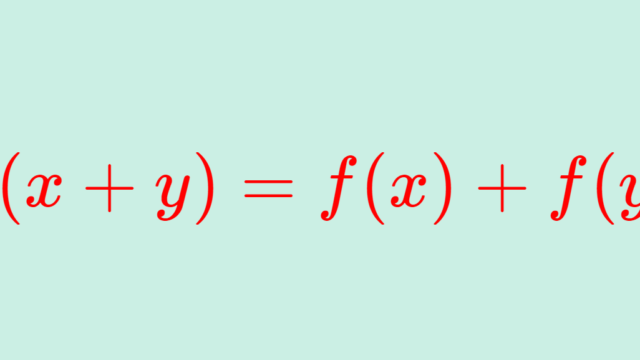 解析学(大学)その他
解析学(大学)その他  線形代数学
線形代数学  線形代数学
線形代数学 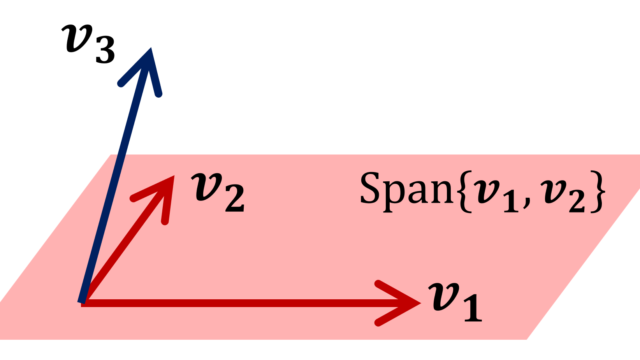 線形代数学
線形代数学 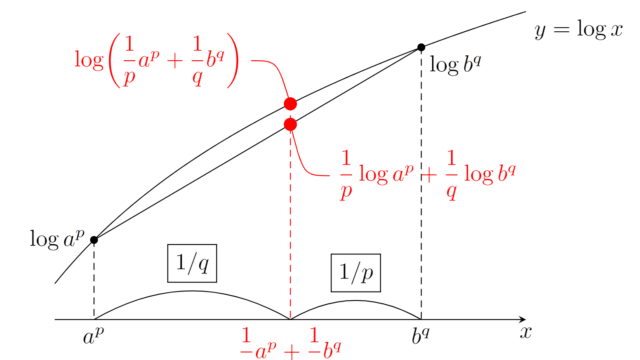 解析学(大学)その他
解析学(大学)その他 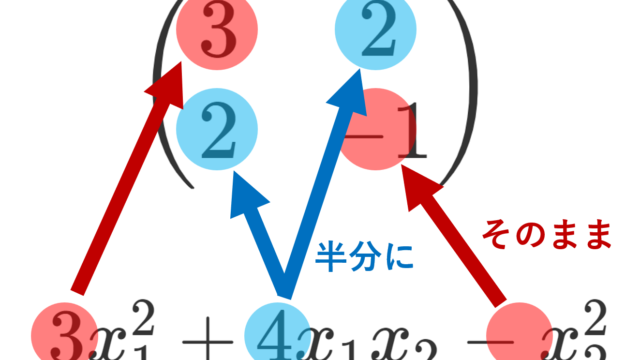 線形代数学
線形代数学 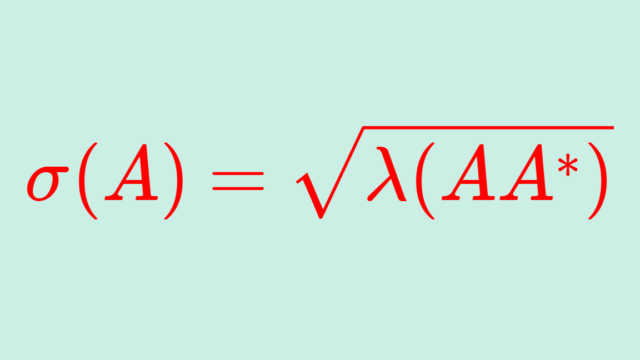 線形代数学
線形代数学  線形代数学
線形代数学 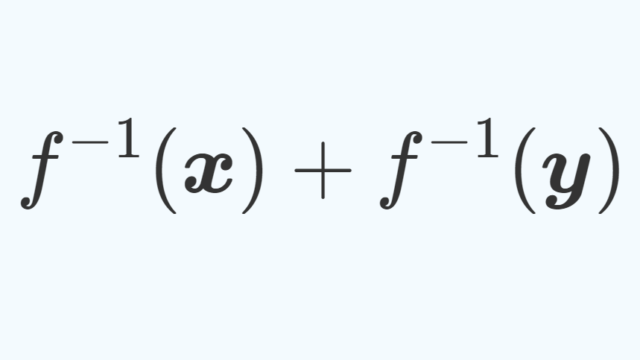 線形代数学
線形代数学 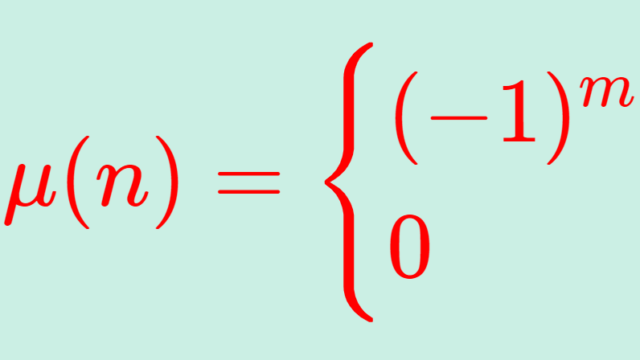 数論
数論