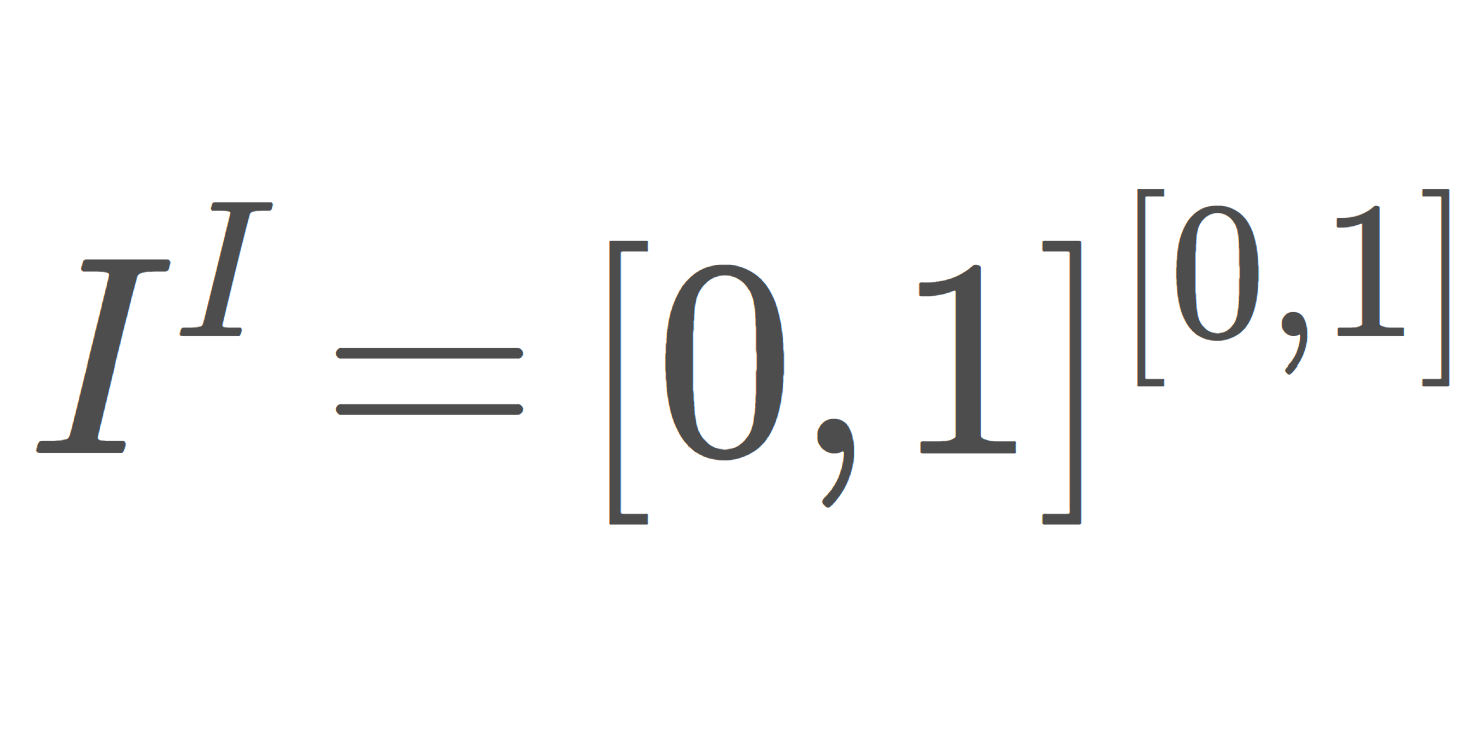I^I の位相的性質～コンパクトだが点列コンパクトでない例～

$I=[0,1]$ を単位区間とします。このとき， $I^I$ とは，関数 $f\colon I\to I$ 全体の集合を指します。 $I^I$ における直積位相を考えると，これはコンパクトだが点列コンパクトでない位相空間の代表例です。 $I^I$ の位相的性質を解説しましょう。

I^I の位相
I^I の位相的性質
関連する記事
参考

I^I の位相

$I=[0,1]$ を単位区間とし，通常の位相が入っているとします。このとき，直積集合の定義から，

\large\color{red} I^I =\prod_{i\in I} I = \{ f\mid f\colon I\to I \}

すなわち， $I^I$ は関数 $f\colon I\to I$ 全体の集合を指します。

$I^I$ に入る直積位相を考えましょう。 $i\in I$ とし， $\color{red}\large { p_i} \colon I^I\ni f\mapsto f(i)\in I$ を自然な射影とします。直積位相の定義と性質より，次のことが分かります。

$I^I$ における直積位相

$I^I$ における直積位相は， $k\ge 1,\; i_1, \ldots, i_k \in I$ とし，さらに $U_1,\ldots, U_k \subset I$ を開集合としたときの

\begin{aligned} B&=p^{-1}_1(U_1)\cap \cdots \cap p^{-1}_k (U_k) \\ &= \{f\colon I\to I\mid f(i_1)\in U_1,\ldots, f(i_k)\in U_k\} \end{aligned}

の形の集合たちの集まり $\mathcal{B}$ を開基とする位相である。すなわち，任意の開集合 $U\subset I^I$ と任意の $x\in U$ に対し， $x\in B\subset U$ となる $B\in \mathcal{B}$ が存在する。

$I^I$ の直積位相は，各点収束の位相である。すなわち，点列 (またはネット(有向点族)) $(f_n)\subset I^I$ が $f_n\to f$ in $I^I$ となる必要十分条件は，各 $i\in I$ に対し， $f_n(i)\to f(i)$ in $I$ となることである。

すべて以下の記事で解説しています。

ポイントは， $I^I$ における開集合上の点 $f$ は，有限個の点 $i_1, \ldots, i_k$ しか行き先を制限されていないということです。それ以外の点 $i\in I\setminus \{i_1, \ldots, i_k\}$ では， $0$ から $1$ までのどんな値を取ってもかまいません。

I^I の位相的性質

可算公理・分離公理・コンパクト性・連結性を順番に紹介しましょう。

I^I と可算公理

第一可算	第二可算	可分
×	×	〇

第一可算でないことが示せれば，第二可算でもないです。

証明

第一可算でないこと

仮に第一可算とし， $f\in I^I$ のまわりの可算な基本近傍系を $\{B_n\}$ とする。直積位相の定義より，各 $n$ について，有限個の $i\in I$ を除いて $p_i (B_n) =I$ のはずである。有限集合の可算個の和集合が高々可算集合であることと， $I$ が非可算集合であることから，任意の $n\ge 1$ に対して $p_{i'}(B_n)=I$ となる $i'\in I$ が存在する。

$f(i')\in U_{i'}\subsetneq I$ となる開集合 $U_{i'}$ をとると， $p_{i'}^{-1}(U_{i'})$ は $f$ の開近傍となる。しかし， $f\in B_n \subset p_{i'}^{-1}(U_{i'})$ となる $n\ge 1$ は存在しないので，矛盾である。ゆえに第一可算でない。

可分であること

$[0,1]$ は可分であり，可分空間の高々連続体濃度個の直積は可分であるので，示された。

証明終

I^I と分離公理

$T_0, T_1, T_2$ (ハウスドルフ空間)	$T_3$	$T_4$	$T_5$
〇	〇	〇	×

本記事では， $T_0$ から $T_5$ は以下のように定義しています。この定義は文献によって変わりますから，注意してください。

名称	定義
$T_0$ コルモゴロフ空間 (Kolmogorov space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ または $x\notin O_y,\, y\in O_y$ となる開集合 $O_y$ の少なくとも一方が取れる
$T_1$	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ と $x\notin O_y, \,y\in O_y$ となる開集合 $O_y$ の両方が取れる
$T_2$ ハウスドルフ空間 (Hausdorff space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset$ となる開集合 $O_x, O_y$ が取れる
$T_3$	任意の閉集合 $F$ と任意の点 $x\in X\setminus F$ に対して， $F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset$ となる開集合 $O_F, O_x$ が取れる
$T_4$	任意の2つの互いに素な空でない閉集合 $F,G\subset X$ に対して， $F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset$ となる開集合 $O_F, O_G$ が取れる
$T_5$	$\overline{A}\cap B=A\cap \overline{B}=\emptyset$ をみたす任意の2つの空でない集合 $A,B\subset X$ に対して， $A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset$ となる開集合 $O_A, O_B$ が取れる。これは，任意の部分空間が $T_4$ になることと同値

証明

$T_0,T_1,T_2,T_3$ 空間であること

$I=[0,1]$ は $T_0,T_1,T_2,T_3$ 空間であり， $T_0,T_1,T_2,T_3$ 空間の直積はまた $T_0,T_1,T_2,T_3$ 空間なのでわかる。

$T_4$ 空間であること

後で述べるが， $I^I$ はコンパクトであり，コンパクトハウスドルフ空間（コンパクト $T_2$ 空間）は $T_4$ であるから，示された。

$T_5$ 空間でないこと

$A=\{ 1/n\mid n\ge 1\}$ とすると， $A\cong \!\mathbb{Z}$ (離散位相) である（ $\cong\!$ は同相(位相同型)の意味）であるため， $A^I\cong \!\mathbb{Z}^I$ である。

詳細は省略するが， $\mathbb{Z}^I$ は $T_4$ でないため， $A^I\subset I^I$ は $T_4$ でない部分集合である。よって， $I^I$ は $T_5$ でない。

証明終

$\mathbb{Z}^I$ が $T_4$ でないことは省略しますが，たとえば， $A_m$ を各 $n\in \mathbb{Z}\setminus \{m\}$ に対し， $f(i)=n$ となる $i\in I$ が高々1個しかない $f\colon I\to \mathbb{Z}$ 全体の集合とすると， $A_0\cap A_1=\emptyset$ で， $A_0, A_1$ はどちらも閉集合ですが， $A_0, A_1$ を開集合で分離することはできません。

I^I とコンパクト性

コンパクト	点列コンパクト
〇	×

冒頭にも述べましたが， $I^I$ はコンパクトだが点列コンパクトでないものの代表例です。本ページのメインテーマです。点列コンパクトとは，任意の点列が収束部分点列をもつことを言います。

コンパクトであることは， $I=[0,1]$ がコンパクトであることと，チコノフの定理 (Tychonoff’s theorem) により直ちにわかります。点列コンパクトでないことを示しましょう。

点列コンパクトでない証明

点列コンパクトであると仮定する。このとき， $(f_n)\subset I^I$ を， $f_n(i) =$ ( $i$ を2進展開したときの小数第 $n$ 位の数) と定める。ただし， $1.0000\cdots_{(2)} = 0.1111\cdots_{(2)}$ などについては左辺を採用する。

もし，収束部分列 $(f_{n_k})\subset (f_n)$ が存在すると仮定する。直積位相 $I^I$ は各点収束位相であったことに注意する。 $\alpha \in I$ を，2進展開したときの小数第 $n_{2k}$ 位 ( $k\ge 1$ ) を $1$ ，それ以外が $0$ となる数とすると，数列 $\{ f_{n_k}(\alpha)\}\subset I$ は $0,1,0,1,0,1\ldots$ という風になり， $I$ 上で収束しない。これは矛盾である。よって示された。

証明終

$I^I$ はコンパクトなので，可算コンパクトです。よって，任意の点列が集積点をもつので，上の証明で現れる $(f_n)$ も集積点 $f \in I^I$ をもちます。言い換えると， $f$ の任意の開近傍 $U\subset I^I$ に対して， $f_n\in U$ となる $n$ が無数に存在します。

よってこれは，点列が集積点をもつからといって，そこに収束する部分列をもつとは限らない例にもなっています。また，ネット(有向点族)の知識があれば， $f$ に収束する $(f_n)$ の部分ネットがあるはずです。よって，点列が収束部分列をもたないが，収束部分ネットをもつ例にもなっています。収束部分ネットの構成は，一般に「ネットが集積点をもてば，そこに収束する部分ネットが存在する」証明から分かりますが，これについてはまた別の機会に紹介しましょう。

なお，実際に集積点 $f$ が何であるかは，選択公理を用いて，たとえばコンパクト空間とコンパクト集合について詳しくの定理4の1. $\implies$ 2.の証明から存在が分かりますが，明示的にかけるかは調べた限りわかりませんでした。