集合 A の凸包とは,A を含む最小の凸集合を指します。これについて,定義と具体例と性質を述べましょう。
凸包とは
定義(凸包)
A\subset\mathbb{R}^n に対し, A を含む最小の凸集合を凸包 (convex hull) という。本記事ではこれを \color{red} \operatorname{Conv}(A) とかくことにする。
A\subset\mathbb{R}^n としましたが, A\subset V で, V を \mathbb{R} 上ベクトル空間としても構いません。
一応凸集合の定義を確認しておきましょう。
C\subset \mathbb{R}^n が凸集合 (convex set) であるとは,
\begin{aligned}&\boldsymbol{x_1},\boldsymbol{x_2}\in C\\&\implies (1-\theta)\boldsymbol{x_1}+\theta \boldsymbol{x_2} \in C \; (0\le\theta\le 1) \end{aligned}
が成り立つことを言う。
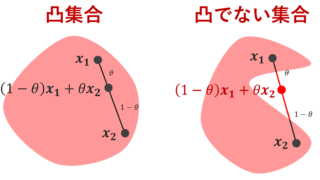
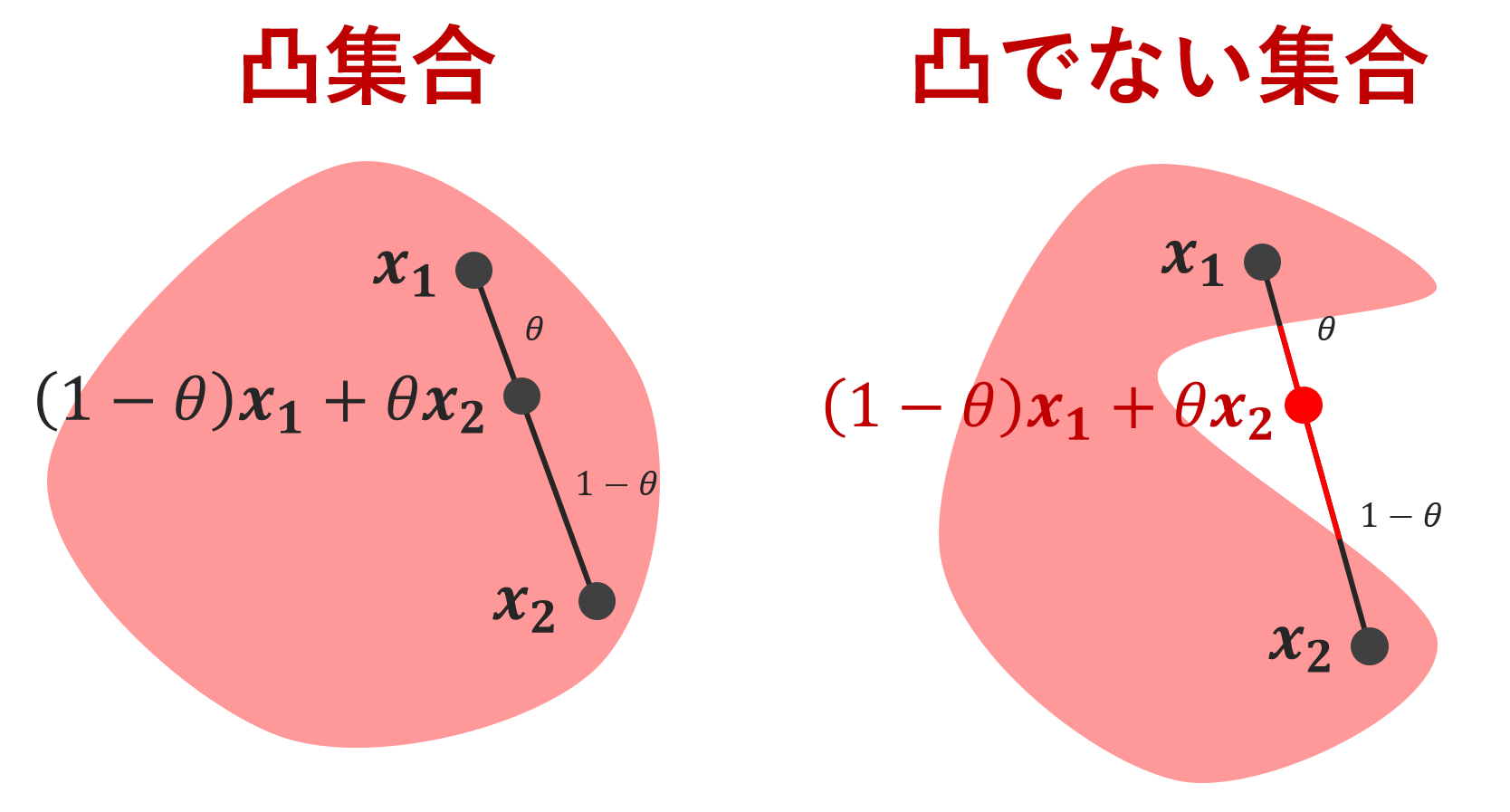
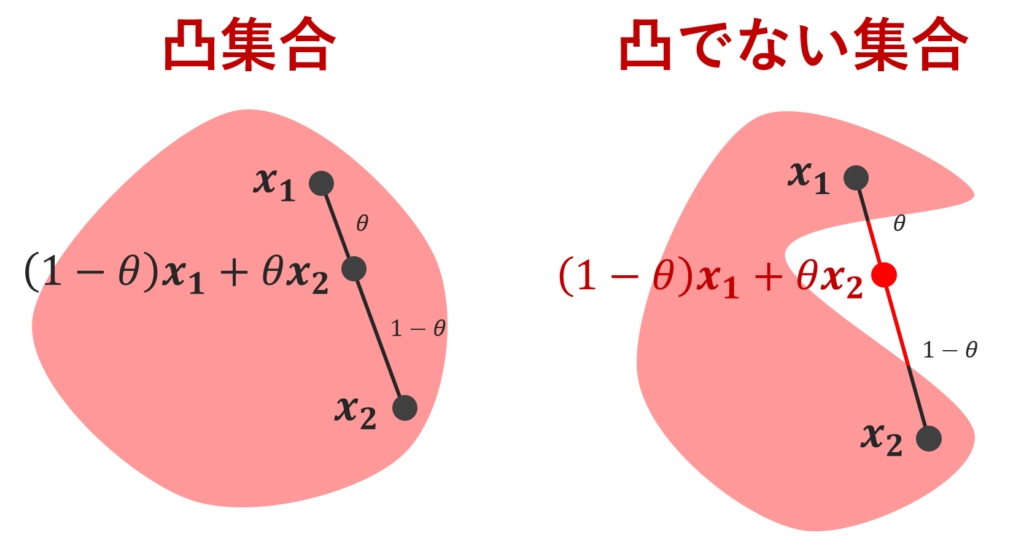
凸集合とそうでない集合の例は,以下の絵が分かりやすいでしょう。
詳しくは,以下の記事で解説しています。
凸包の具体例
以下では, 2 次元の集合における,元の図形と,その凸包の具体例を挙げましょう。

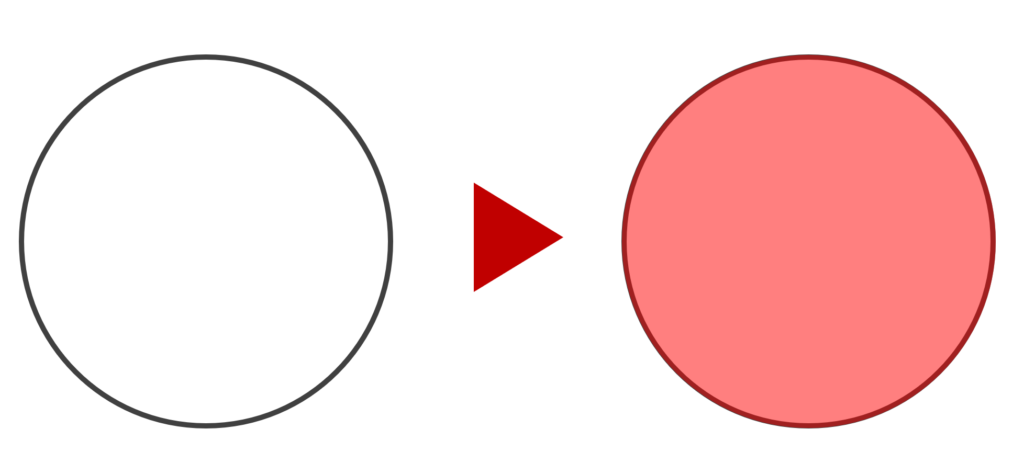

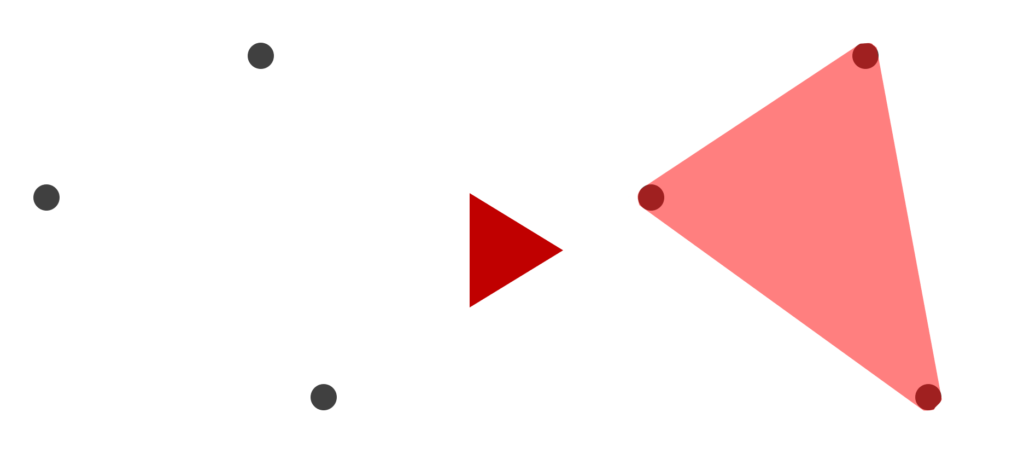
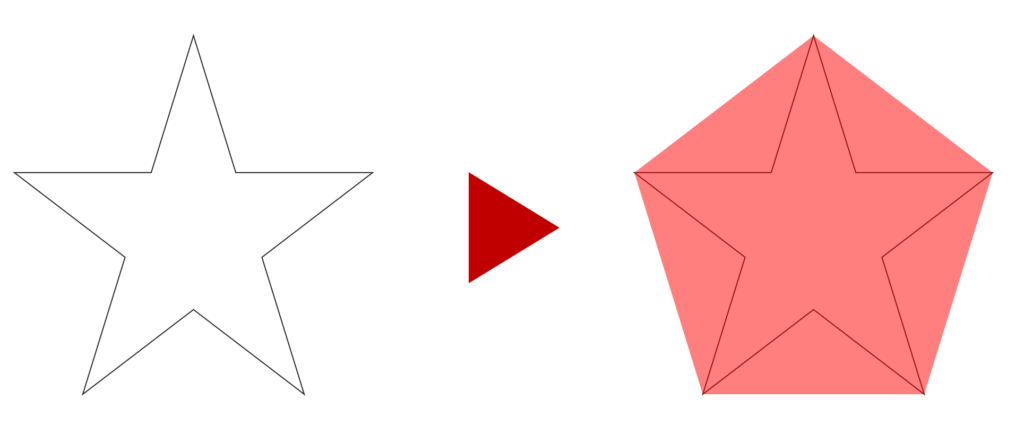
凸包の性質
凸包の簡単な性質を挙げましょう。
定理(凸包の性質)
A,B\subset \mathbb{R}^n とする。
- \operatorname{Conv}(A) は, A を含むすべての凸集合の共通部分である。
- A\subset B \implies \operatorname{Conv}(A)\subset \operatorname{Conv}(B).
- \operatorname{Conv}(\operatorname{Conv}(A))=\operatorname{Conv}(A).
A,B\subset\mathbb{R}^n としましたが, A,B\subset V で, V を \mathbb{R} 上ベクトル空間としても構いません。
どの証明も簡単ですから,証明しておきましょう。
証明
1.について
A を含むすべての凸集合の共通部分はまた凸集合になる。よってこれは A を含む最小の凸集合である。
2.について
A\subset \operatorname{Conv}(B) かつ \operatorname{Conv}(B) は凸より,\operatorname{Conv}(A)\subset \operatorname{Conv}(B).
3.について
定義より, \operatorname{Conv}(A)\subset \operatorname{Conv}(\operatorname{Conv}(A)).
\operatorname{Conv}(A)\subset \operatorname{Conv}(A) かつ右辺は凸より, \operatorname{Conv}(\operatorname{Conv}(A))\subset \operatorname{Conv}(A).
証明終