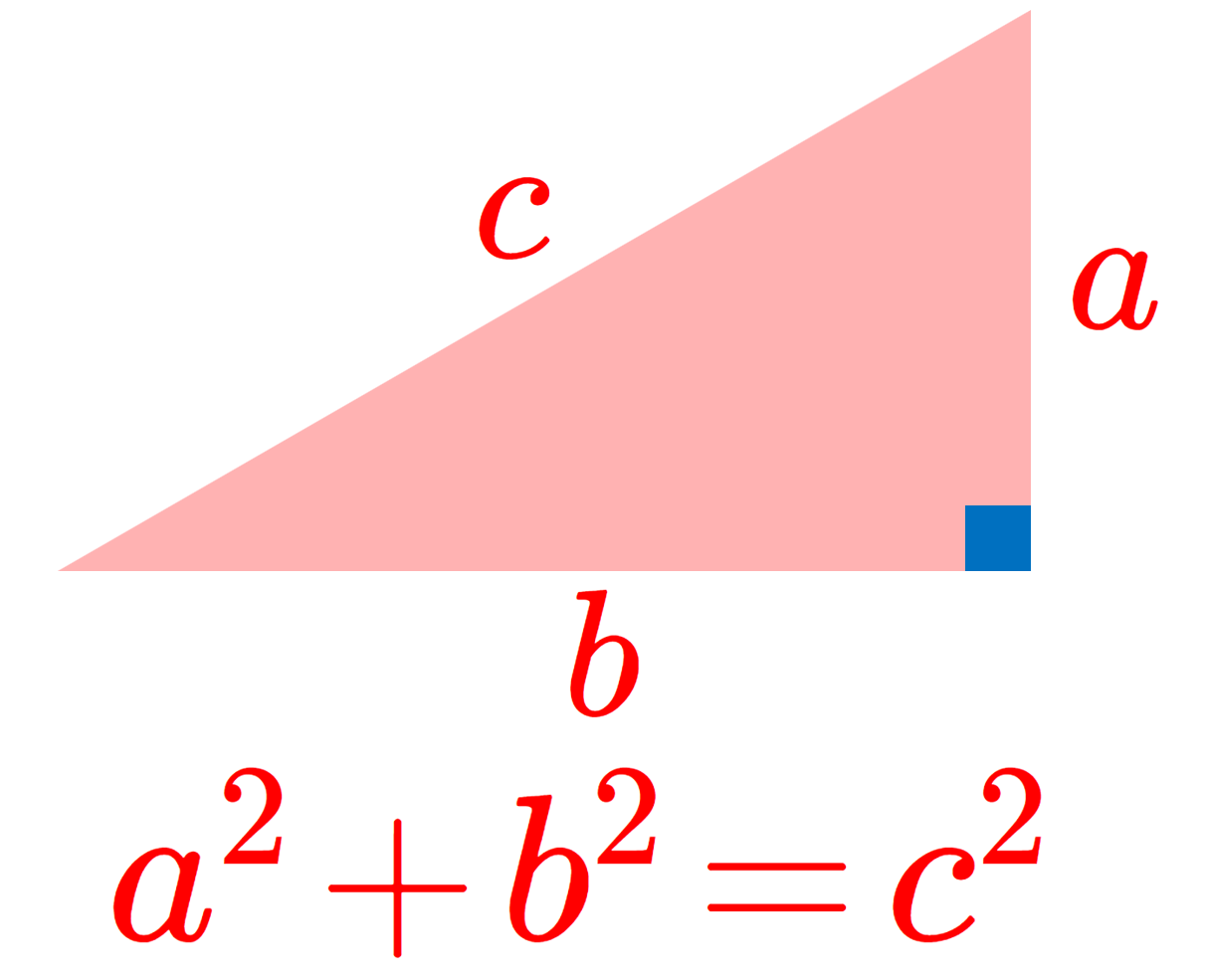a^2+b^2=c^2 をみたすような正の整数 (a,b,c) をピタゴラス数といいます。特に, a,b,c の3数の最大公約数が 1 であるピタゴラス数 (a,b,c) を原始ピタゴラス数といいます。
原始ピタゴラス数は(いい感じの条件を課すと)
a= m^2-n^2,\quad b= 2mn, \quad c= m^2+n^2
(m,n は正の整数)とかけることが知られています。これについて掘り下げていきましょう。
ピタゴラス数・原始ピタゴラス数
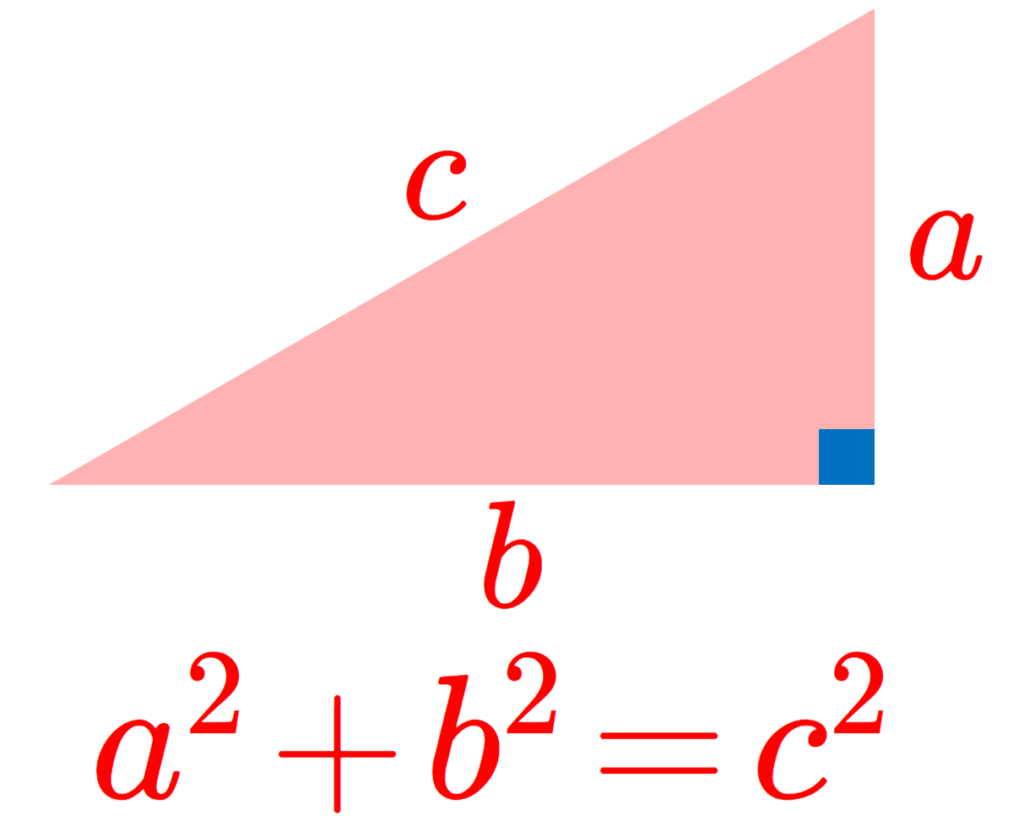
ピタゴラス数・原始ピタゴラス数の定義
定義(ピタゴラス数・原始ピタゴラス数)
\color{red}\boldsymbol{a^2+b^2=c^2} となる正の整数の組 (a,b,c) をピタゴラス数 (Pythagorean triple) という。特に \operatorname{gcd}(a,b,c)=1 のとき,原始ピタゴラス数 (primitive Pythagorean triple) という。
(a,b,c) をピタゴラス数とするとき,正の整数 k に対して, (ka,kb,kc) もピタゴラス数になります。これは本質的には同じもので,面白くないです。よって,最大公約数が 1 のみのものを考え,それを「原始ピタゴラス数」というわけです。
各辺の長さが整数の直角三角形はピタゴラス数ですね。
原始ピタゴラス数の例
原始ピタゴラス数の例を述べておきましょう。
\begin{gathered}(3,4,5), (5,12,13), (8,15,17), (7,24,25), \\ (20,21,29), (9,40,41), (12,35,37), \\(11,60,61), (28,45,53) , (33, 56,65), \cdots \end{gathered}よりたくさんの例を知りたい場合は,ピタゴラス数一覧【10000以下全て1593個】を参照してください。
ピタゴラス数の性質
- 原始ピタゴラス数を 3,4,5 で割った余りに関する話
- 原始ピタゴラス数の解(求め方)
について順番に述べましょう。
ピタゴラス数とmod
定理1(ピタゴラス数と {}\bmod{})
(a,b,c) を a^2+b^2=c^2 をみたす原始ピタゴラス数とする。このとき,
- a,b のいずれか一方のみ 3 の倍数になる。
- a,b のいずれか一方のみ 4 の倍数になる。
- a,b,c のいずれか一つのみ 5 の倍数になる。
これらより,ピタゴラス数の積 abc は必ず 60 の倍数になることも分かりますね。
略証
a,b,c の3つの数の最大公約数が 1 であることに注意する。
{}\bmod 3 で考えると,x が整数のとき, x^2\equiv 0,1 \pmod 3 である。 a^2, b^2 が {}\bmod 3 で 0,1 と合同な場合4通りを場合分けしてすべて考えると,題意が示される。
{}\bmod 4 で考えると,x が整数のとき, x^2\equiv 0,1 \pmod 4 である。 a^2, b^2 が {}\bmod 4 で 0,1 と合同な場合4通りを場合分けしてすべて考えると,題意が示される。
{}\bmod 5 で考えると,x が整数のとき, x^2\equiv 0,1,4 \pmod 5 である。 a^2, b^2 が {}\bmod 4 で 0,1,4 と合同な場合9通りを場合分けしてすべて考えると,題意が示される。
証明終
ピタゴラス数の解(求め方)
上の証明と同様にすると, \operatorname{gcd}(a,b,c)=1 が a^2+b^2=c^2 をみたすとき, a,b の片方は奇数で,もう一方が偶数であることが分かります。ここでは,a が奇数で,b を偶数としましょう。また,このとき明らかに c は奇数です。
定理2(ピタゴラス数の表現)
a^2+b^2=c^2 をみたす原始ピタゴラス数 (a,b,c) であって, b が偶数であるものは,
\large \color{red}\begin{aligned} a&= m^2-n^2,\\ b&= 2mn, \\ c&= m^2+n^2 \end{aligned}
とかける。ただし, m>n>0 は整数で, m, n は互いに素, m,n のいずれかは偶数である。
逆に,このようにかける a,b,c は原始ピタゴラス数である。
証明
前半について
a,b,c の3数の最大公約数が 1 であることと, a^2+b^2=c^2 より, a,b,c はどの2つも互いに素である(背理法でスグ分かる)。 b は偶数より, b=2b_1( b_1 は整数)とできる。
a^2+4b_1^2=c^2 より, 4b_1^2=(c+a)(c-a) である。ここで, c-a, c+a 最大公約数は 1 または 2 である(なぜなら, d=\operatorname{gcd}(c+a,c-a) とし, dx=c+a, \, dy=c-a とすると,d(x+y)=2c, \, d(x-y)=2a で, a,c は互いに素なので, d は 2 の約数である)。
また, a,c は共に奇数より, c+a,c-a は共に偶数である。
以上から, (c+a)/2,(c-a)/2 は互いに素な整数で, b_1^2=\dfrac{c+a}{2}\cdot \dfrac{c-a}{2} より,
\frac{c+a}{2}=m^2,\quad \frac{c-a}{2}=n^2
( m, n は互いに素な正の整数)とかける。 (c+a)/2>(c-a)/2 より, m>n>0 である。これを a,c について解くと,
これを a^2+b^2=c^2 に代入すると, b=2mn も得る。 a,c は奇数であり,定理1より b は 4 の倍数なので, m,n のいずれかは偶数である。以上から,示された。
後半について
a=m^2-n^2, \, b=2mn, \, c=m^2+n^2 とすると a^2+b^2=c^2 をみたすことは明らか。 \operatorname{gcd}(a,b,c)=1 を示す。 \operatorname{gcd}(a,b)=1 を示せばよい。 m,n の偶奇が異なるので,明らかに a,b の偶奇も異なる。 よって奇素数 p が a,b をともに割り切ることがないことを示せばよい。よって奇素数 p が a,b の公約数とする。
p が b=2mn を割り切る(これを \color{red} p\mid 2mn とかく)ので, p \mid m または p\mid n である。 p\mid m とする。これと p\mid m^2-n^2 より, p\mid n^2 となって, p\mid n がわかるが,これは m,n が互いに素であることに矛盾する。同様に p\mid n を仮定しても同じである。
証明終
この定理を基に,ピタゴラス数と m,n の関係は以下のようになります。
| a=m^2-n^2 | b=2mn | c=m^2+n^2 | m | n |
|---|---|---|---|---|
| 3 | 4 | 5 | 2 | 1 |
| 5 | 12 | 13 | 3 | 2 |
| 15 | 8 | 17 | 4 | 1 |
| 7 | 24 | 25 | 4 | 3 |
| 21 | 20 | 29 | 5 | 2 |
| 9 | 40 | 41 | 5 | 4 |
| 35 | 12 | 37 | 6 | 1 |
| 11 | 60 | 61 | 6 | 5 |
| 45 | 28 | 53 | 7 | 2 |
| 33 | 56 | 65 | 7 | 4 |
よりたくさんの例を知りたい場合は,ピタゴラス数一覧【10000以下全て1593個】を参照してください。
ピタゴラス数と円・直線
x^2+y^2=1 をみたす有理数 x, y\in\mathbb{Q} を求めよという問題は, x=a/c,\, y=b/c とすることで a^2+b^2=c^2 にできますから,ピタゴラス数の問題だと思えます。実際, 0 以上の整数 m, n ( m^2+n^2>0)を用いて
\color{red}x=\frac{m^2-n^2}{m^2+n^2} ,\quad y=\frac{2mn}{m^2+n^2}
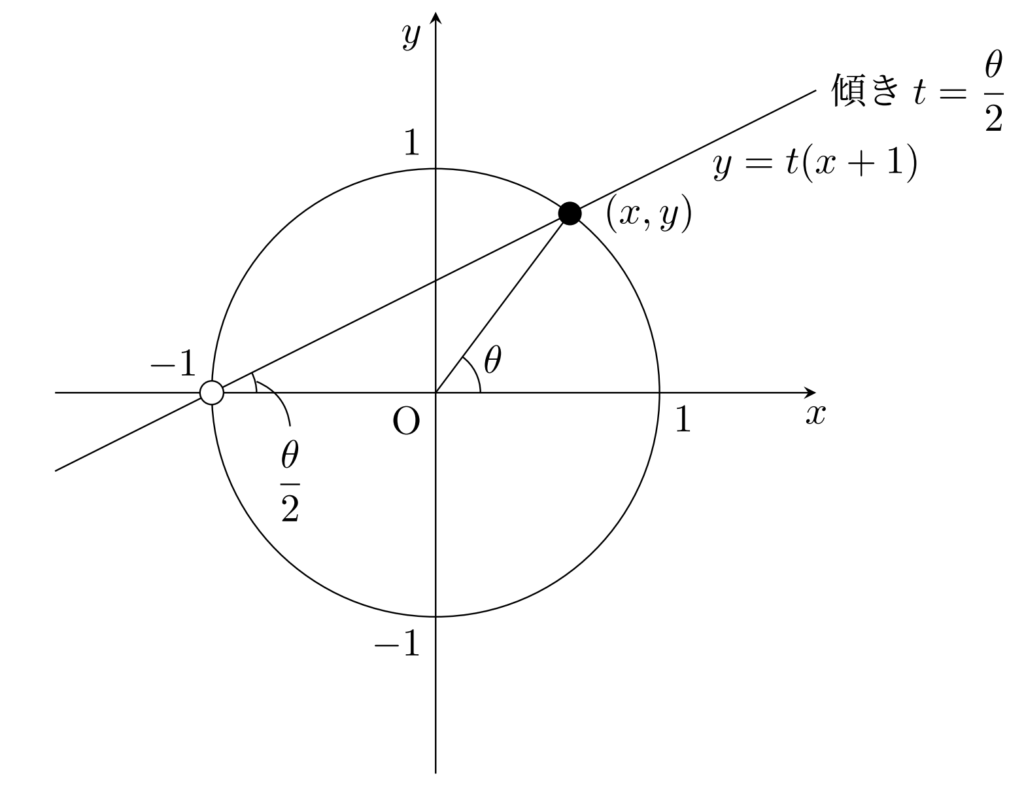
と表せます。これは, m=0 のとき (-1,0) で, m\ne 0 のとき,以下のように (-1,0) を通り傾き n/m の直線と, x^2+y^2=1 の (-1,0) 以外の交点と思えます。
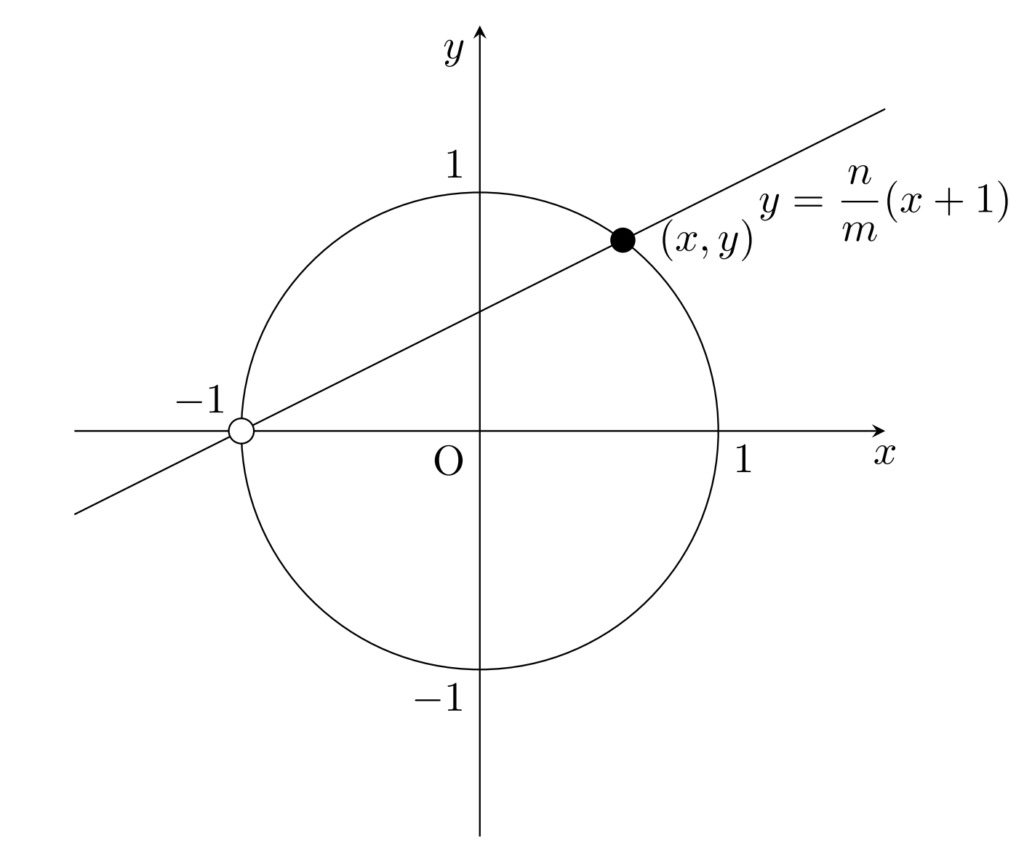
あるいは, t=n/m とすると, x^2+y^2=1\;(x,y\in\mathbb{Q}) の解は
\color{red}(x,y)=(-1,0), \left(\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2}\right) \quad (t\in\mathbb{Q})
とかくことも可能です。これは図を活用して,以下のように簡単に証明することができます。
x^2+y^2=1 の有理数解が直前の赤字の式になる証明
(x,y)=(-1,0), \left(\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2}\right)\; (t\in\mathbb{Q}) は明らかに有理数解である。逆に,有理数の組 (x,y) が x^2+y^2=1 をみたすとする。
x=-1 のとき, y=0 である。 x\ne -1 のとき, t=y/(x+1) とおくと, t\in\mathbb{Q} であり, y=t(x+1) であるが,これは図のように点 (x,y) が直線 y=t(x+1) 上にあることを意味している。
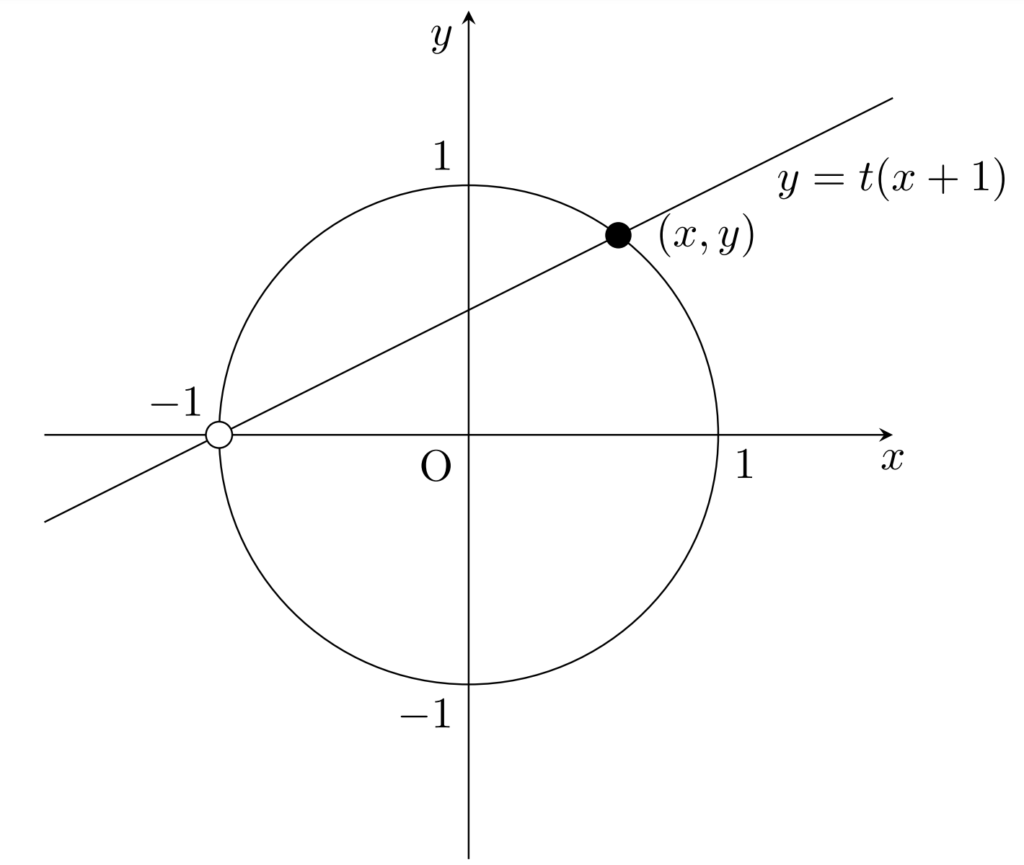
y=t(x+1) と x^2+y^2=1 を連立して解くと,
(x,y)=\left(\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2}\right)
となる。
証明終
さらに, t=\tan(\theta/2) と定めると,
(x,y)=\left(\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2}\right)=(\cos\theta, \sin\theta)
となり,三角関数とも密接に関係していることが分かります。これは,以下の図で説明可能です。