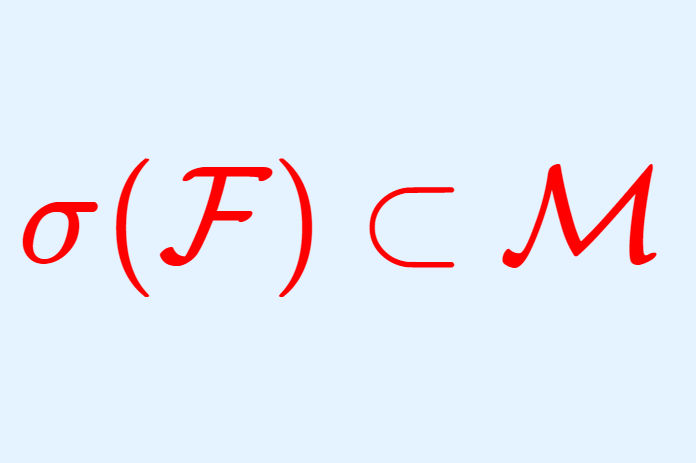集合の部分集合族が「単調族」であるとは,無限個の集合の上昇列や下降列に関して閉じていることを言います。単調族について,その詳しい定義と,有名で大切な単調族定理の証明を行いましょう。
単調族の定義
定義(単調族)
X を空でない集合とし, \emptyset\ne \mathcal{M}\subset 2^X をその部分集合族とする。 \mathcal{M} が
- \color{red} \{A_n \} \subset\mathcal{M},\; A_1 \subset A_2 \subset A_3 \subset \cdots \implies \bigcup_{n = 1}^\infty A_n \in \mathcal{M}
- \color{red} \{A_n\} \subset \mathcal{M},\; A_1\supset A_2\supset A_3 \supset \cdots \implies \bigcap_{n = 1}^\infty A_n \in \mathcal {M}
の両方をみたすとき, \mathcal{M} を単調族 (monotone class) という。
1,2.の条件はそれぞれ
- \color{red}\{A_n\}\subset\mathcal{M},\; A_n \uparrow A\implies A\in\mathcal{M}
- \color{red}\{A_n\}\subset \mathcal{M},\; A_n \downarrow A\implies A\in\mathcal{M}
と書かれることもあります。
たとえば, \mathbb{R} 上の一点集合のみの集合族は単調族です。また,開区間(空集合含む)・閉区間(一点集合含む)・半開区間全体の集合も単調族です。
「 \mathcal{F} がσ-加法族 \implies \mathcal{F} が単調族」は明らかでしょう。また,
\mathscr{M}_{\mathcal{F}}=\{ \mathcal{F}\subset\mathcal{M}\colon \mathcal{M}\text{ is monotone}\}
を,集合族 \mathcal{F} を含む単調族全体の集合としましょう。 2^X\in \mathscr{M}_{\mathcal{F}} なのでこれは空ではありません。このとき,\mathcal{M}_0 = \bigcap_{\mathcal{M}\in\mathscr{M}_{\mathcal{F}}} \mathcal{M} と定めると, \mathcal{M}_0 も単調族になることは容易に確認可能です。これは,\mathcal{F} を含む最小の単調族ですね。
この議論から,ある集合族を含む最小の単調族を考えることが可能です。
単調族定理とその証明
有名な単調族定理を紹介し,証明しましょう。
定理(単調族定理)
X を空でない集合とし,その部分集合族 \mathcal{F}\subset \mathcal{M} について, \mathcal{F} が有限加法族かつ \mathcal{M} が単調族であるとする。このとき,
\large \color{red} \sigma(\mathcal{F})\subset \mathcal{M}
が成立する。ただし, \sigma(\mathcal{F}) とは \mathcal{F} から生成されるσ-加法族を表す。特に,有限加法族を含む最小の単調族はσ‐加法族である。
特に後半部分は大切で,σ-加法族の証明が難しいときに,有限加法族かつ単調族であることを証明すればよいということですね。
有限加法族の定義を復習しておきましょう。有限加法族とは,以下の3つをみたすものです。
- \emptyset\in\mathcal{F}
- A\in\mathcal{F}\implies A^c\in\mathcal{F}
- \{A_k\}_{k=1}^n \subset\mathcal{F}\implies \bigcup_{k=1}^n A_k\in\mathcal{F}
3.の n を \infty に変えると,σ-加法族の定義になります。
証明
\mathcal{F} を含む最小の単調族を \mathcal{M}(\mathcal{F}) と表すことにすると, \mathcal{M}(\mathcal{F}) = \sigma(\mathcal{F}) を示せばよい。σ-加法族なら単調族なので, \mathcal{M}(\mathcal{F}) \subset\sigma(\mathcal{F}) は明らか。よって, \mathcal{M}(\mathcal{F}) がσ-加法族であることを示せばよい。
\emptyset \in\mathcal{M}(\mathcal{F}) は \emptyset\in \mathcal{F} よりすぐわかる。
A\in\mathcal{M}(\mathcal{F})\implies A^c \in\mathcal{M}(\mathcal{F}) について
\mathcal{M}_c = \{ A\in\mathcal{M}(\mathcal{F})\mid A^c\in\mathcal{M}(\mathcal{F})\}
とおくと, \mathcal{M}_c が \mathcal{F} を含む単調族であることは容易。よって \mathcal{M}(\mathcal{F})\subset \mathcal{M}_c なので,示せた。
\{A_n\} \subset\mathcal{M}(\mathcal{F})\implies \bigcup_{n=1}^\infty A_n\in\mathcal{M}(\mathcal{F}) について
A_1, A_2 \in\mathcal{M}(\mathcal{F})\implies A_1\cap A_2 \in\mathcal{M}(\mathcal{F}) を示せば, A\in\mathcal{M}(\mathcal{F})\implies A^c\in\mathcal{M}(\mathcal{F}) であることと,単調族の定義から,直ちに赤字が従うので,これを示す。一般の A\in\mathcal{M}(\mathcal{F}) に対し,
\mathcal{M}_A =\{ M\in\mathcal{M}(\mathcal{F})\mid A\cap M\in\mathcal{M}(\mathcal{F})\}
と定める。まず F\in\mathcal{F} とすると,有限加法族の定義より, \mathcal{F}\subset \mathcal{M}_F であり,また明らかに \mathcal{M}_F は単調族である。よって \mathcal{M}(\mathcal{F})\subset\mathcal{M}_F となる。
次に A\in\mathcal{M}(\mathcal{F}) とすると,直前の議論より \mathcal{F}\subset\mathcal{M}_A であり,また明らかに \mathcal{M}_A は単調族である。よって \mathcal{M}(\mathcal{F})\subset \mathcal{M}_A となる。これは青字を意味する。
証明終
証明は少しテクニカルですね。この証明手法は,測度論ではよく使われます。
関連する記事
単調族定理と同じくらい重要な定理として,ディンキン族定理があります。以下で解説しています。