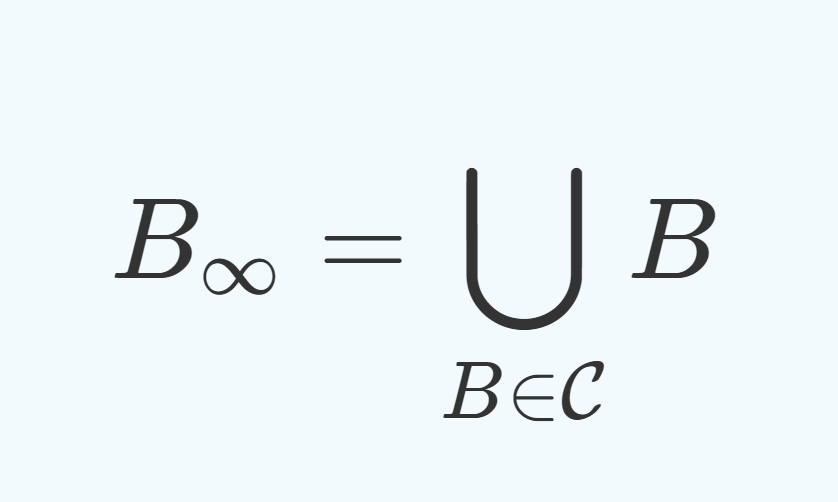\operatorname{Span} S とは集合 S の一次結合(線形結合)によってできるベクトル空間(線形包linear span)を指します。これは, S を含む最小のベクトル空間になります。Spanの定義と具体例を確認していきましょう。
Spanの意味とは【線形結合】
定義(\operatorname{Span})
V を K 上ベクトル空間, S\subset V をその部分集合とする。
\color{red} \operatorname{Span} S = \left\{ \sum_{i=1}^n k_i \boldsymbol{v_i} \middle|\begin{aligned} \boldsymbol{v_1},\dots, \boldsymbol{v_n}\in S,\\ k_1,\dots, k_n \in K, \end{aligned}\; n\ge 1 \right\}
を S の線形包 (linear span) あるいは S で張られたベクトル空間という。
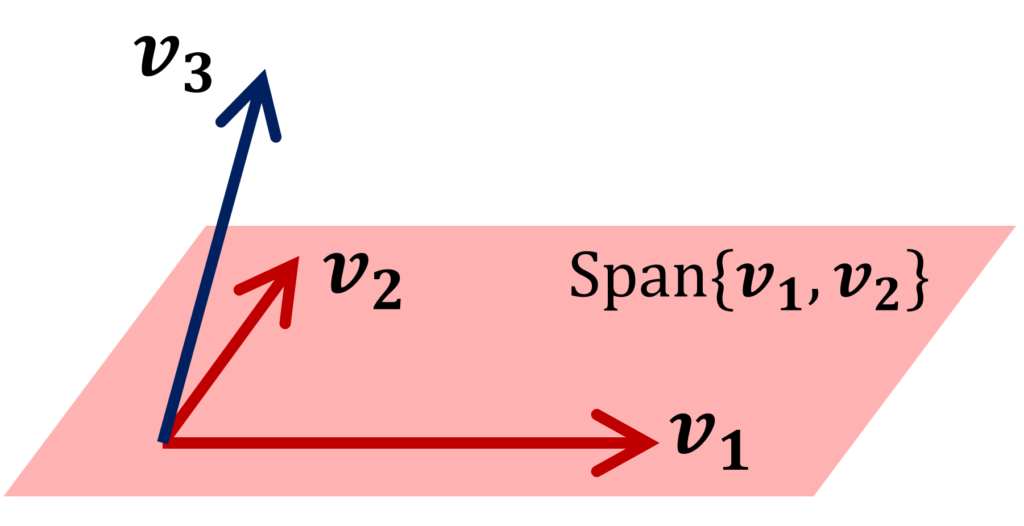
S=\{\boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n}\} (有限集合)のときは単に
\operatorname{Span} S=\{ k_1\boldsymbol{v_1}+\cdots +k_n\boldsymbol{v_n}\mid k_i\in K\}
なだけです。一方で, S が無限集合のときは,その中から有限個を選んだ一次結合(線形結合)全体の集合を指します。
\operatorname{Span} の定義から明らかに S\subset \operatorname{Span} S であり,また \operatorname{Span} S は V の部分ベクトル空間になります。特に, S を含む最小のベクトル空間です。
Spanの具体例
例1.
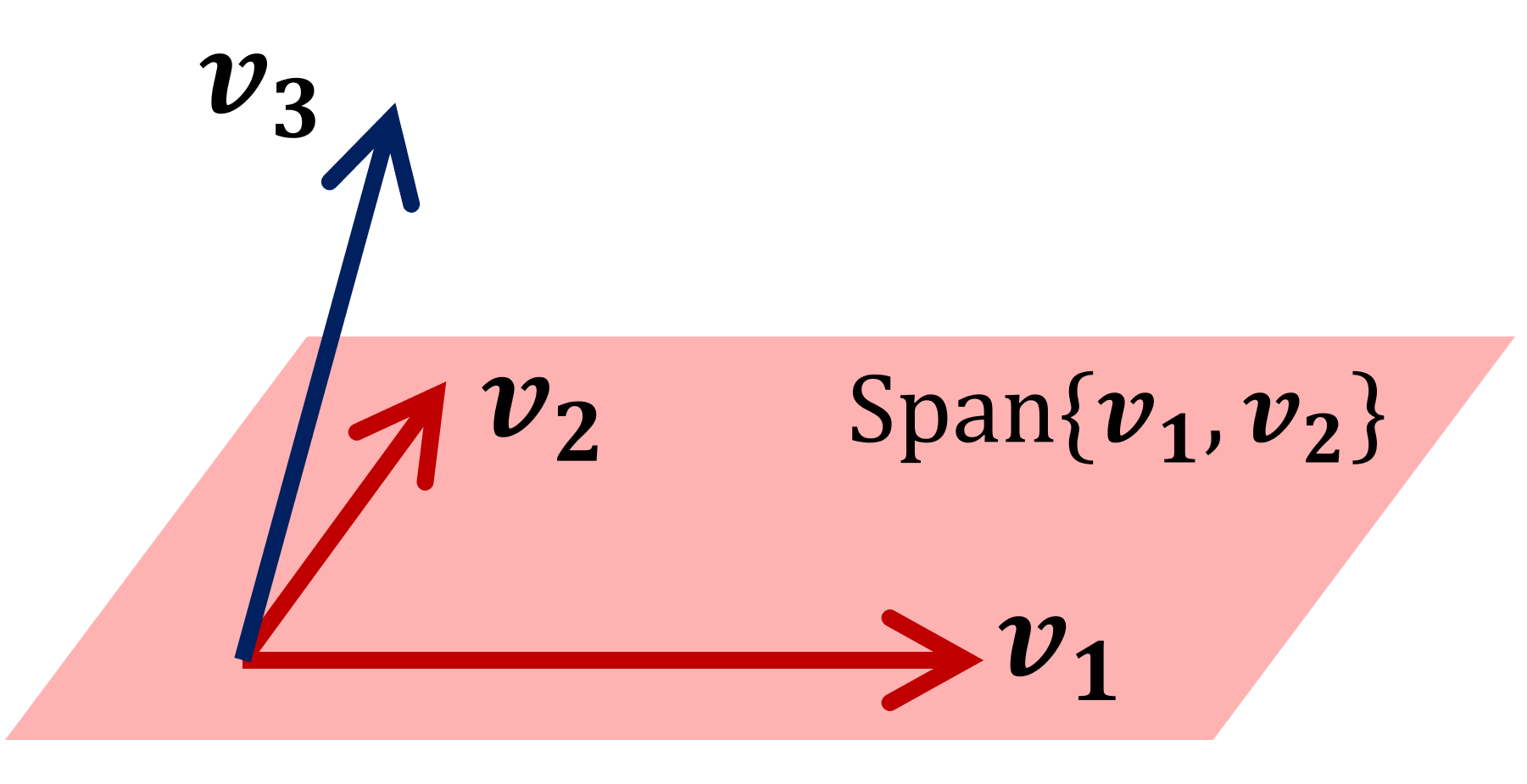
\R^3=\{(x,y,z)\mid x,y,z\in\R\} を \R 上ベクトル空間とする。このとき, \boldsymbol{v_1}=(1,0,0), \boldsymbol{v_2}=(1,1,0) とすると,
\begin{aligned}\operatorname{Span} \{\boldsymbol{v_1}\}&= \{ (x,0,0)\mid x\in\R\}\\ \operatorname{Span} \{\boldsymbol{v_2}\}&= \{ (x,x,0)\mid x\in\R\}\\ \operatorname{Span} \{\boldsymbol{v_1},\boldsymbol{v_2}\}&= \{ (x,y,0)\mid x,y\in\R\} \end{aligned}
である。
分かりやすい例ですね。他にも, \boldsymbol{v_3}=(2,0,0) とすると,
\operatorname{Span} \{ \boldsymbol{v_1},\boldsymbol{v_3}\} = \{(x,0,0)\mid x\in \R\}
になります。
例2.
実数列 (x_n) 全体の集合を \R 上のベクトル空間とみて,
\begin{aligned}\boldsymbol{e_1}&=(1,0,0,\dots) ,\\ \boldsymbol{e_2}&=(0,1,0,\dots),\\ &\vdots \end{aligned}
とする。このとき,
であり,さらに
要するに,有限個の x_i を除いてすべて x_i=0 をみたす実数列 x_i 全体を指す。
後半については特に注意してください。 \operatorname{Span}S の S が無限集合のときは,そこから有限個を選んできたものの一次結合(線形結合)ですから, \operatorname{Span} \{\boldsymbol{e_1},\boldsymbol{e_2},\dots\} は有限個の x_i 以外は全て x_i=0 となる実数列全体となります。
なお,バナッハ空間のような位相が定義されたベクトル空間では,Spanの閉包 \overline{\operatorname{Span} S} を考えることも多いです。