 関数解析学
関数解析学 正規直交系・正規直交基底
正規直交系とは,大きさが1であり,互いに直交するベクトルの集まりを指します。また,正規直交基底(完全正規直交系)とは,正規直交系で,かつ全てのベクトルがそれらを用いて表現可能なことをいいます。正規直交系・正規直交基底について,定義と具体例を見ていきましょう。
 関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学 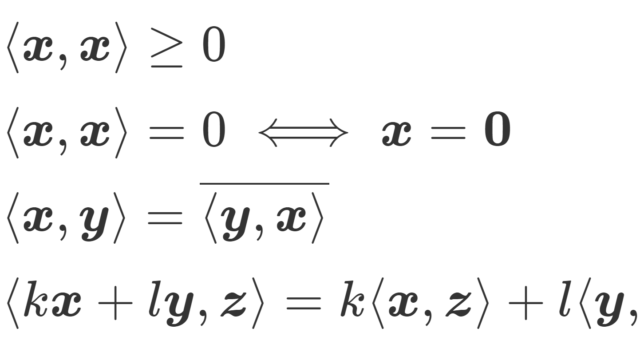 関数解析学
関数解析学 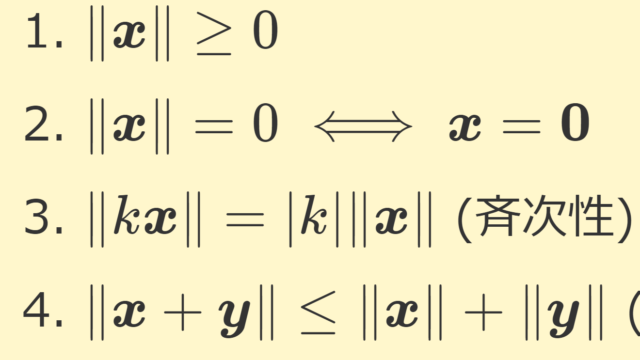 関数解析学
関数解析学 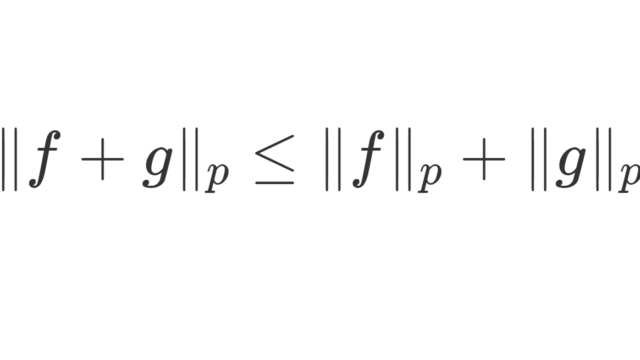 関数解析学
関数解析学 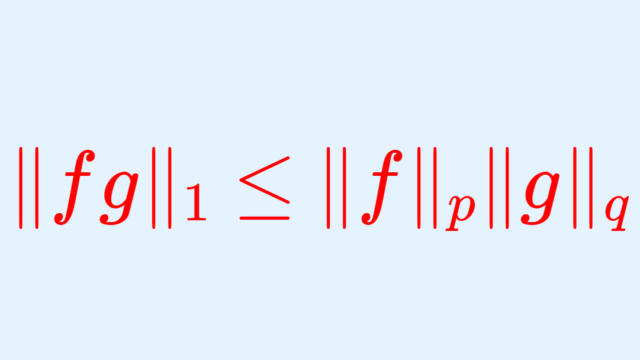 関数解析学
関数解析学