 集合と位相
集合と位相 相対位相と部分位相空間の定義・具体例5つ・性質5つ
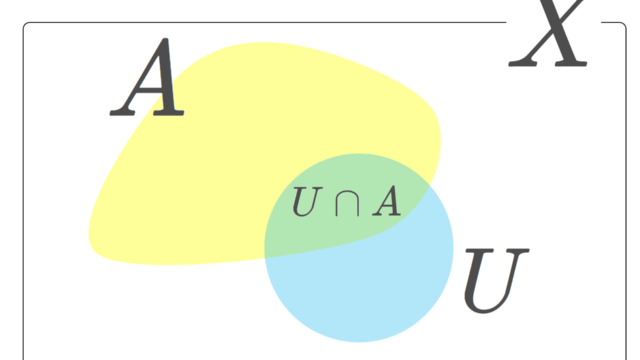
位相空間論における相対位相とは,位相空間の部分集合に入る位相のことです。元の位相と同じ性質を引き継ぐこともあれば,全く異なる性質を持つこともあります。相対位相・部分位相空間について,その定義と具体例・性質とその証明をしていきます。
 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 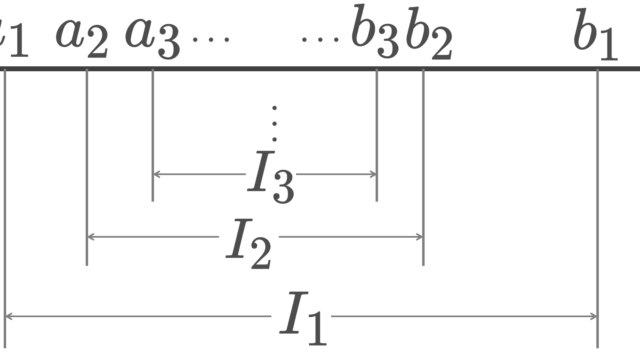 解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他 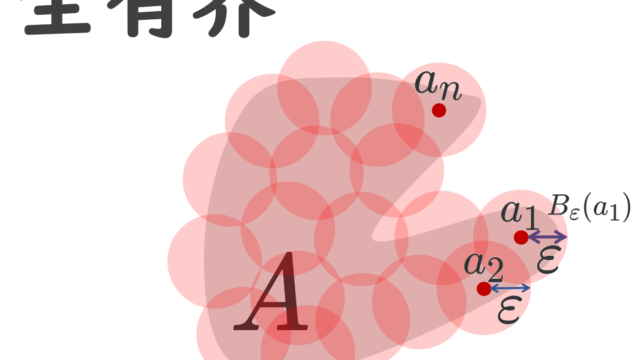 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相