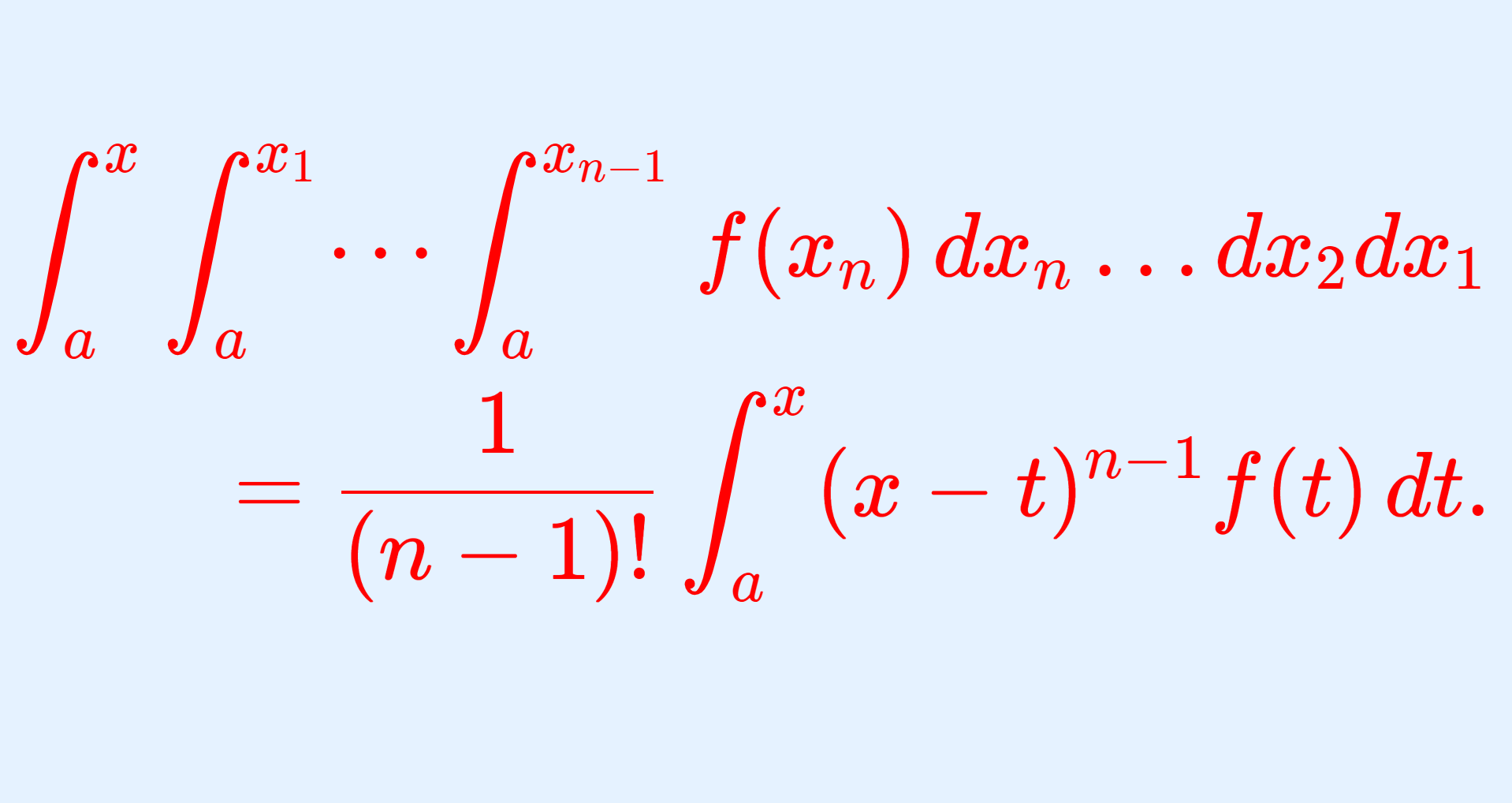反復積分 \displaystyle \int_a^x \int_a^{x_1} \int_a^{x_2}\dots \int_a^{x_{n-1}} f(x_n) \,dx_n\dots dx_3dx_2dx_1 は,1回の積分で書き表すことができます。この定理について紹介し,証明しましょう。
反復積分に関するコーシーの公式
定理(反復積分に関するコーシーの公式)
f \colon \mathbb{R}\to \mathbb{R} を連続関数, a<x とする。このとき,
\color{red}\begin{aligned} \int_a^x \int_a^{x_1} \dots \int_a^{x_{n-1}} f(x_n) \,dx_n\dots dx_2dx_1 \\ = \frac{1}{(n-1)!}\int_a^x (x-t)^{n-1} f(t)\, dt \end{aligned}
が成立する。
驚くべき定理かもしれませんね。これを証明しましょう。
反復積分に関するコーシーの公式の証明
証明
帰納法で示そう。 n=1 のとき,明らかに等式は成立する。
n で成立していると仮定して, n+1 で成立することを示そう。このとき,
\begin{aligned} & \int_a^{x} \int_a^{x_1}\dots \int_a^{x_{n}} f(x_{n+1}) \,dx_{n+1}\dots dx_2dx_1\\ &= \int_a^{x} \frac{1}{(n-1)!}\int_a^{x_1} (x_1-t)^{n-1} f(t)\, dtdx_1. \end{aligned}
フビニの定理より,積分の順序を交換して,
であるから, n+1 でも性質することが分かって,結論を得る。
証明終
積分の順序交換さえ理解できれば,証明はそれほど難しくないかもしれませんね。