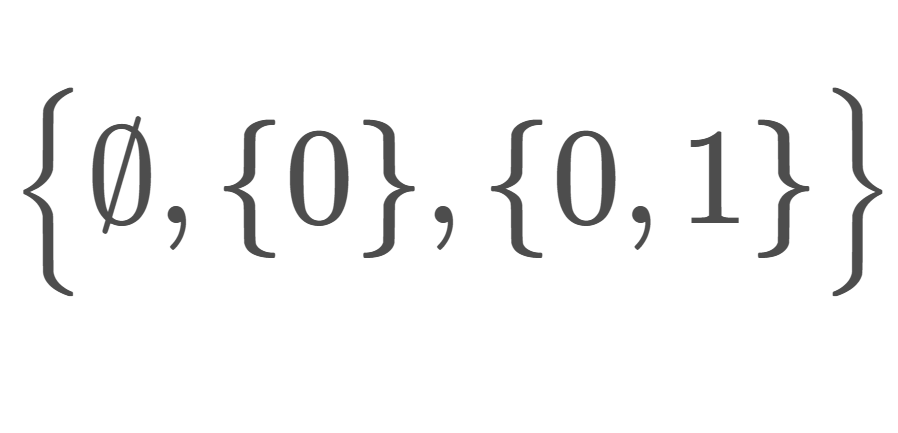補有限位相と補可算位相について掘り下げる

補有限位相とは，補集合が有限集合である部分集合全体を開集合系とする位相で，補可算位相は，補集合が高々可算集合である部分集合全体を開集合系とする位相です。

特に補有限位相は，位相空間論を学ぶ際によく取り上げられる具体例の一つで， $T_1$ 空間だがハウスドルフ空間でないなど，初学者にとって教育的な意味をもつ例です。

補有限位相と補可算位相について，その定義と性質を証明付きでまとめましょう。

補有限位相・補可算位相の定義
1. 補有限位相の性質
2. 補可算位相の性質
参考

補有限位相・補可算位相の定義

定義（補有限位相・補可算位相）

$X$ を空でない集合とする。

\mathcal{O}_f=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\}

を，補集合が有限集合である部分集合全体（と $\{\emptyset\}$ との和集合）とすると， $(X,\mathcal{O}_f)$ は位相空間になる。この位相を補有限位相 (cofinite topology, finite complement topology) という。

\mathcal{O}_c=\{\emptyset \}\cup \left\{O\subset X\middle|\begin{gathered} X\setminus O \text{ is at most} \\ \text{countable}\end{gathered}\right\}

を，補集合が高々可算集合である部分集合全体（と $\{\emptyset\}$ との和集合）とすると， $(X,\mathcal{O}_c)$ は位相空間になる。この位相を補可算位相 (cocountable topology, countable complement topology) という。

補有限位相について， $X$ が有限集合のとき，あるいは補可算位相について， $X$ が高々可算集合のとき，ただの離散空間になるだけです。よって，補有限位相については $X$ は無限集合，すなわち可算または非可算集合とし，補可算位相については $X$ は非可算集合とします。

さて，ここから補有限位相・補可算位相の性質を述べていきますが，先に主な性質を一覧にまとめておきます。

	可算集合上の補有限位相	非可算集合上の補有限位相	非可算集合上の補可算位相
第一可算	〇	×	×
第二可算	〇	×	×
可分	〇	〇	×
$T_0, T_1$ 空間	〇	〇	〇
$T_2, T_3, T_4, T_5$ 空間	×	×	×
コンパクト	〇	〇	×
点列コンパクト	〇	〇	×
リンデレーフ	〇	〇	〇
連結・局所連結	〇	〇	〇
弧状連結	×	〇連続体仮説を認める	×

順番に見ていきましょう。

分離公理は，本サイトでは以下の定義を採用しています。これは文献によって異なります。

名称	定義
$T_0$ コルモゴロフ空間 (Kolmogorov space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ または $x\notin O_y,\, y\in O_y$ となる開集合 $O_y$ の少なくとも一方が取れる
$T_1$	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ と $x\notin O_y, \,y\in O_y$ となる開集合 $O_y$ の両方が取れる
$T_2$ ハウスドルフ空間 (Hausdorff space)	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset$ となる開集合 $O_x, O_y$ が取れる
$T_3$	任意の閉集合 $F$ と任意の点 $x\in X\setminus F$ に対して， $F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset$ となる開集合 $O_F, O_x$ が取れる
$T_4$	任意の2つの互いに素な閉集合 $F,G\subset X$ に対して， $F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset$ となる開集合 $O_F, O_G$ が取れる
$T_5$	$\overline{A}\cap B=A\cap \overline{B}=\emptyset$ をみたす任意の2つの集合 $A,B\subset X$ に対して， $A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset$ となる開集合 $O_A, O_B$ が取れる

1. 補有限位相の性質

定理1（補有限位相の性質）

$X$ は無限集合， $(X,\mathcal{O}_f)$ には補有限位相が入っているとする。このとき，

$X$ が可算ならば，第二可算公理をみたす。したがって，第一可算公理もみたす。非可算ならば，第一可算公理をみたさない，したがって第二可算公理もみたさない。
$X$ は可分である。
$X$ は $T_0,T_1$ 空間であるが，ハウスドルフ空間( $T_2$ 空間)でない。 $T_3,T_4, T_5$ 空間でもない。 $X$ は $T_1$ 分離公理をみたす最小の(最粗の)位相である。
$X$ はコンパクトかつ点列コンパクトである。
$X$ は hyperconnected であるから，連結だし，局所連結でもある。
$X$ が可算ならば，弧状連結ではない。 $X$ が非可算かつ連続体仮説をみたすとすると，弧状連結である。

補有限位相は， $T_1$ 空間であるがハウスドルフ空間( $T_2$ 空間)でない例として重要です。また，非可算集合のときは，第一可算公理をみたさない例としても重要です。

1.1. Xが可算なら第二可算であり，非可算なら第一可算でないこと

証明

まず前半を示す。 $X$ を可算とすると， $X$ の各元を番号付けして， $X= \{x_n\}$ かつ $m\ne n$ ならば $x_m \ne x_n$ とできる。

A_{m,n} =\{x_m\}\cup (X\setminus \{ x_1, x_2, \ldots, x_n\})

と定めると， $\{ A_{m,n}\}_{m,n=1}^\infty$ は $X$ の開基になっている。実際， $O\subset X$ を任意の空でない開集合， $x\in O$ を $O$ の任意の点とする。このとき，ある $m\ge 1$ が存在して， $x=x_m$ とかける。また， $X\setminus O$ は有限集合なので，ある $j\ge 1$ と $n_1, n_2, \ldots, n_j\ge 1$ が存在して，

X\setminus O=\{ x_{n_1}, x_{n_2},\ldots, x_{n_j}\}

とあらわせる。 $n=\max\{ n_1, n_2,\ldots, n_j\}$ とすると，

x\in A_{m, n} \subset O

とかけるので， $\{ A_{m,n}\}_{m,n=1}^\infty$ は $X$ の開基であることが示せた。 $\{ A_{m,n}\}_{m,n=1}^\infty$ は可算個の元からなるので，第二可算である。

次に後半を示す。背理法を用いる。 $X$ を非可算集合とし，第一可算公理をみたすと仮定する。 $x\in X$ とし， $\mathcal{B}_x$ を $x$ の可算な基本近傍系とする。

$x$ のすべての開近傍 $N$ に対して，ある $B\in\mathcal{B}_x$ が存在して， $x\in B\subset N$ とできることと，すべての開近傍の共通部分は $\{x\}$ であることから， $\bigcap_{B\in\mathcal{B}_x} B=\{x\}$ である。両辺補集合を考えると，

\bigcup_{B\in\mathcal{B}_x} X\setminus B =X\setminus\{x\}

である。 $X\setminus B$ は有限集合であり，その可算個の和であるから，左辺は高々可算であるが，右辺は非可算なので，これは矛盾している。よって， $X$ は第一可算でない。

証明終

1.2. Xが可分であること

証明

$X$ が可算集合のときは明らか。 $X$ が非可算であるとする。 $A\subset X$ を可算集合とすると， $\overline{A}=X$ となるから，やはり可分である。

証明終

1.3. X はT0, T1だが，T2, T3, T4, T5でないこと

$T_0$ 空間の定義は【位相空間】コルモゴロフ空間(T0空間)の定義と具体例を， $T_1$ 空間の定義は【位相空間】T1空間の定義・具体例と性質をみてください。

証明

$a,b\in X$ を異なる2点とすると， $X\setminus\{a\}, X\setminus\{b\}$ はどちらも開集合で，前者は $a$ を含まず $b$ を含み，後者はその逆である。よって $T_1$ 空間である。 $T_1\implies T_0$ より(→【位相空間】T1空間の定義・具体例と性質)， $T_0$ 空間でもある。

$X$ の任意の2つの空でない開集合は，必ず共通部分を持つ（すなわち後で出てくる hyperconnected) ので， $T_2,T_3, T_4, T_5$ 空間の定義はみたさない。

また， $T_1$ 空間であることと，1点集合は必ず閉集合になることは同値であり(→【位相空間】T1空間の定義・具体例と性質)，1点集合が閉集合になる最小の位相は補有限位相なので， $X$ は $T_1$ 分離公理をみたす最小の(最粗の)位相である。

証明終

1.4. Xはコンパクトかつ点列コンパクトであること

注意ですが，コンパクトだからといって点列コンパクトとは言えないし，点列コンパクトだからといってコンパクトとは言えません。

証明

まずコンパクトを示す。 $\mathcal{C}$ を開被覆とし， $C\in\mathcal{C}$ を一つ取る。このとき， $X\setminus C$ は有限集合なので， $X\setminus C=\{x_1, \ldots, x_n\}$ とかける。 $x_1\in C_1, \ldots, x_n \in C_n$ となる $C_1, \ldots, C_n \in\mathcal{C}$ を取ると， $\mathcal{C}_0 =\{C, C_1, \ldots, C_n\}$ は有限部分被覆となっているため，コンパクトは示せた。

次に点列コンパクトを示す。 $\{x_n\}\subset X$ を点列とする。 $x\in X$ が存在して， $x_n=x$ となる $n$ が無限個あるとすると， $\{x_n\}$ は $x$ に収束する部分列を明らかに持つので，そのような $x$ は存在しないと仮定する。

このとき， $\{x_n\}$ は任意の点 $x\in X$ に収束するといえる。実際， $x\in O\subset X$ を開集合とすると， $X\setminus O$ は有限集合であり， $\{x_n\}$ の仮定より，ある $N\ge 1$ が存在して， $n\ge N\implies x_n \in O$ とできるからである。したがって，点列コンパクト性が示せた。

証明終

1.5. Xはhyperconnected，連結，局所連結であること

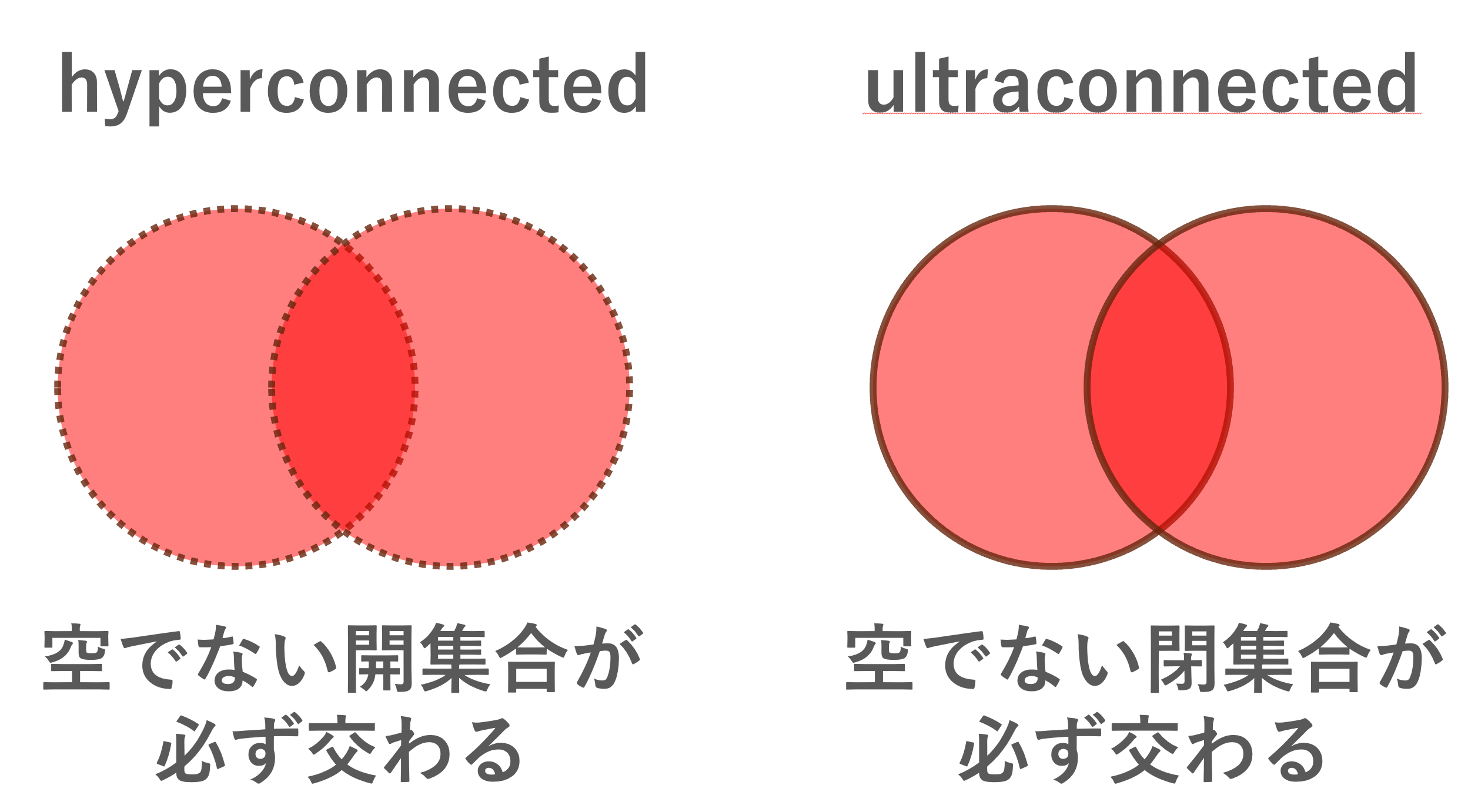
hyperconnected とは，任意の空でない2つの開集合が共通部分をもつことを言いますが，これは明らかです。

hyperconnected なら，連結 (connected) や局所連結 (locally connected) であることは，定義からほぼ明らかです(→hyperconnected(既約位相空間)とultraconnected)。

1.6. Xが可算なら弧状連結ではなく，非可算かつ連続体仮説を認めると弧状連結であること

証明

まず， $X$ が可算集合で，定値写像でない $f\colon [0,1]\to X$ が連続だったとする。このとき， $x\in X$ に対し， $f^{-1}(\{x\})$ は閉集合で，

[0,1] = \bigcup_{x\in X} f^{-1}(\{x\})

は閉集合の2個以上高々可算個の非交和となるが， $[0,1]$ は閉集合の2個以上高々可算個の非交和では表せないことが知られているので，これは矛盾する。よって，弧状連結ではない。同じ理由で，局所弧状連結でもない。

一方で， $X$ が非可算かつ連続体仮説をみたすとすると，異なる2点 $x,y\in X$ に対し， $x,y\in S\subset X$ となる，連続体濃度の集合 $S$ がとれる。このとき， $f(0)=x, f(1)=y$ となる全単射 $f\colon [0,1]\to S$ が取れるが，これは連続写像である。実際， $F\subset S$ を閉集合とすると， $F$ は有限集合なので， $f^{-1}(F)\subset [0,1]$ も有限集合なため， $\ f^{-1}(F)$ は閉集合である。なので $f$ は連続である。

証明終

2. 補可算位相の性質

つづいて，補可算位相の性質も確認しましょう。

定理2（補可算位相の性質）

$X$ は非可算集合， $(X,\mathcal{O}_c)$ には補可算位相が入っているとする。このとき，

$X$ は第一可算公理をみたさない，したがって第二可算公理もみたさない。
$X$ は可分でない。
$X$ は $T_0,T_1$ 空間であるが，ハウスドルフ空間( $T_2$ 空間)でない。 $T_3,T_4, T_5$ 空間でもない。
$X$ はコンパクトでない。点列コンパクトでもない。可算コンパクトでも，可算メタコンパクトでもない。σコンパクトでもない。しかし，リンデレーフである。
$X$ は hyperconnected であるから，連結だし，局所連結でもある。
$X$ は弧状連結ではない。

補可算位相は，補有限位相よりも大きい（細かい・強い）位相です。

1.については，補有限位相で $X$ が非可算なら第一可算でないことと，補可算位相は補有限位相よりも大きい（細かい・強い）ことから従います。

3.は，定理1.3の証明とほぼ同様です。5.も，定理1.5の証明とほぼ同様です。2.と4.と6.のみ考えましょう。

2.2. Xが可分でないこと

証明

$A\subset X$ を高々可算集合とすると， $\overline{A}=A$ であるから，可分でない。

証明終

2.4. Xが点列コンパクト・可算コンパクト・可算メタコンパクト・σコンパクトでないが，リンデレーフであること

まずは定義を確認しておきましょう。

名称	定義
点列コンパクト (sequentially compact)	任意の点列が収束部分列をもつ
コンパクト (compact)	任意の開被覆が有限部分被覆をもつ
可算コンパクト (countably compact)	任意の可算開被覆が有限部分被覆をもつ
リンデレーフ (Lindelöf)	任意の開被覆が可算部分被覆をもつ
σコンパクト (σ-compact)	コンパクト集合の可算和でかける空間
可算メタコンパクト (countably metacompact)	任意の可算開被覆が点有限な(すなわち，各点ごとに有限個の集合でしか覆われていない)部分被覆をもつ
擬コンパクト (pseudocompact)	この上の任意の実連続関数が有界

σコンパクトでなければコンパクトでないし，可算コンパクトでなければコンパクトでないことは明らかです。

証明

点列コンパクトでないことを示す。 $\{x_n\}_{n=1}^\infty \subset X$ を任意の2点が異なる点列とする。任意の $x\in X$ に対して，

O= (X\setminus \{x_n\}_{n=1}^\infty )\cup \{x\}

は $x$ の開近傍であるが， $\{x_n\}$ は $O$ 内に収束しない。よって， $x$ に収束しないので，点列コンパクトではない。

可算コンパクトでないこと・可算メタコンパクトでないことを示す。 $\{x_n\}\subset X$ を可算部分集合としたときに，

C_n = X\setminus \{ x_n, x_{n+1}, x_{n+2},\ldots\}

とおくと， $\{C_n\}$ は可算開被覆であるが，有限部分被覆は存在しないため，可算コンパクトではない。また，点 $x\in X\setminus \{x_n\}_{n=1}^\infty$ においては，任意の部分被覆で点有限でないので，可算メタコンパクトでもない。

σコンパクトでないことを示す。 $A\subset X$ が非可算部分集合であるとき，可算コンパクトでないことを真上で示したので，コンパクトではない。 $A\subset X$ が高々可算集合であるとき， $A$ に入る相対位相は離散位相である。ゆえに， $A$ がコンパクトである必要十分条件は $A$ が有限集合であることである。よって，σコンパクトではない。

リンデレーフを示す。 $\mathcal{C}$ を開被覆とし， $C\in\mathcal{C}$ を一つ取る。このとき， $X\setminus C$ は高々可算集合なので， $X\setminus C=\{x_1, x_2, \ldots \}$ とかける。 $x_1\in C_1, x_2\in C_2,\ldots$ となる $C_1, C_2,\ldots \in\mathcal{C}$ を取ると， $\mathcal{C}_0 =\{C, C_1, C_2, \ldots \}$ は可算部分被覆となっているため，リンデレーフは示せた。

証明終