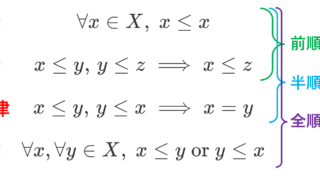辞書式順序とは,順序集合の直積集合に定まる順序の一つで,国語辞書の単語が並ぶ順番と同じような順序のことを言います。まず,有限個の直積における辞書式順序の定義・具体例を紹介し,それから,無限個を含む辞書式順序を考えます。
最後に,整列集合たちの辞書式順序が整列集合になるか否かを考えましょう。
有限個の直積による辞書式順序
定義に半順序集合や全順序集合という言葉を使いますが,あまり難しく考えず,整数の集合とか実数の集合とかアルファベットの集合とか思っておけばよいです。詳しく知りたい場合は,半順序集合・全順序集合の定義・具体例4つとその周辺を参照してください。
以下で,defは「定義 (definition)」の意味です(→定義・公理・定理・命題・補題・系を完全理解しよう)。
定義1(有限個の直積による辞書式順序)
(A_1, \le), (A_2, \le),\ldots, (A_n, \le) を半順序集合(resp. 全順序集合)とする。このとき,直積集合 A=A_1\times A_2\times \cdots \times A_n の2元 (a_1, a_2, \ldots, a_n), (b_1, b_2, \ldots, b_n) に対し,
\begin{aligned}&(a_1,a_2,\ldots, a_n)< (b_1, b_2,\ldots, b_n) \\ & \xLeftrightarrow{\mathrm{def}} \textcolor{red}{a_1 <b_1} \\ & \qquad\text{ or } \textcolor{blue}{a_1=b_1}, \, \textcolor{red}{a_2< b_2} \\ &\qquad\text{ or } \textcolor{blue}{a_1=b_1, \, a_2=b_2}, \, \textcolor{red}{ a_3< b_3} \\ &\qquad \text{ or } \cdots\,\cdots \\ & \qquad \text{ or }\textcolor{blue}{ a_1=b_1, \ldots, a_{n-1}=b_{n-1}},\,\textcolor{red}{ a_n<b_n } \end{aligned}
と定めると, (A, \le) は半順序集合 (resp. 全順序集合)になる。これを, A における辞書式順序 (lexicographical order, dictionary order) という。
考え方としては,左から順に見ていって,まず1番目の要素の順序で大小を決めて,1番目が同じなら2番目の要素の順序で大小を決めて,2番目が同じなら3番目の要素の順序で大小を決めて……としていくイメージです。
例1.
整数全体の集合 \mathbb{Z} に通常の大小を入れた全順序集合5つの直積 \mathbb{Z}^5=\mathbb{Z}\times \mathbb{Z}\times \mathbb{Z}\times \mathbb{Z}\times \mathbb{Z} 上の辞書式順序について,
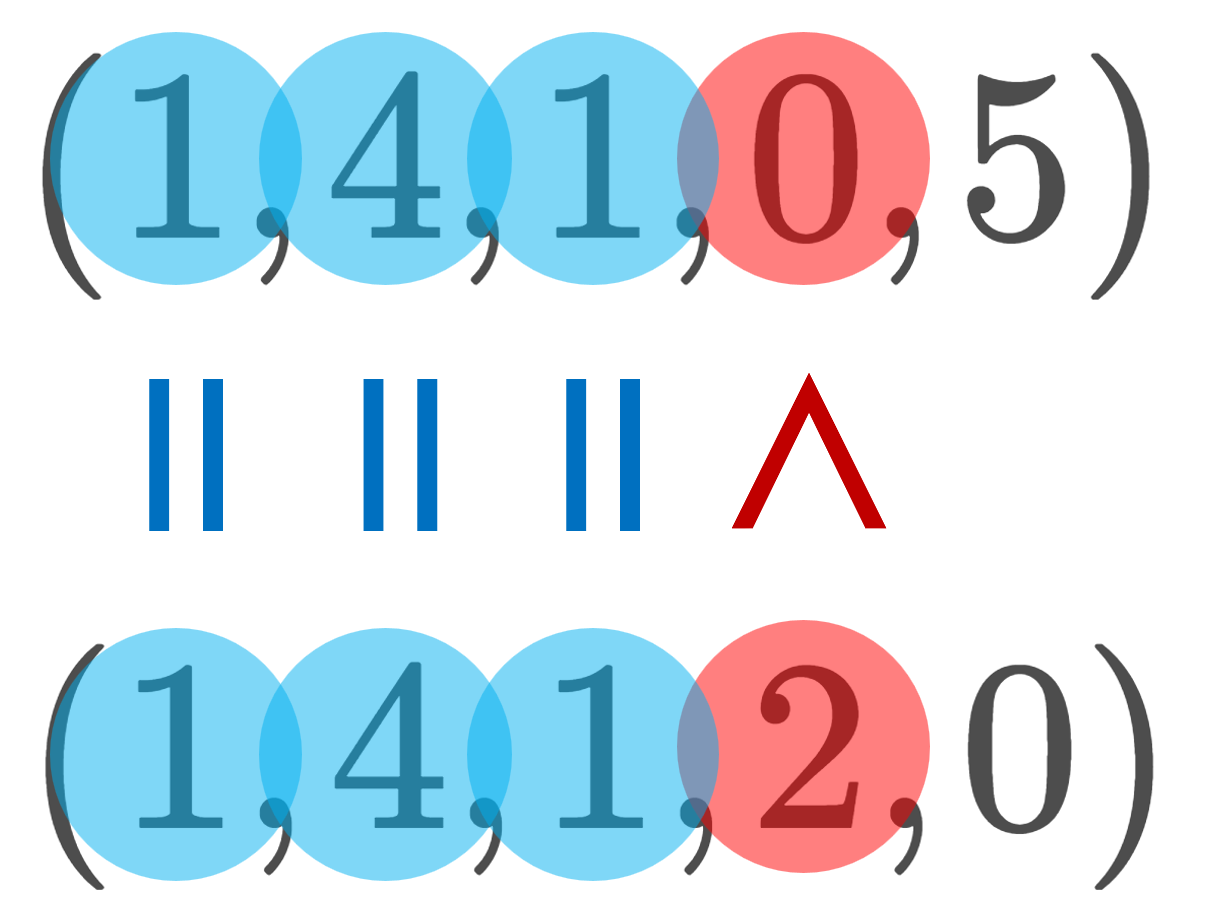
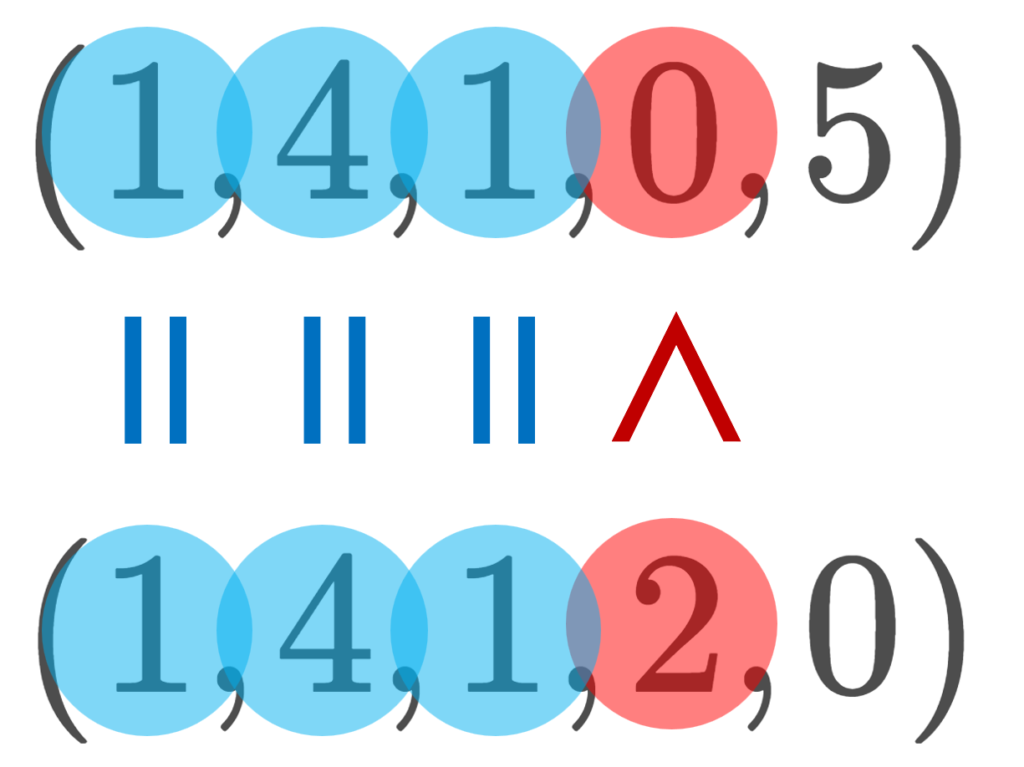
(0, 9, 9, 7, 0) < (1, 4, 1, 0, 5) < (1, 4, 1, 2, 0)
である。

辞書式順序と呼ばれる理由は,上の順序は,国語辞書で単語が並ぶ順番と一致しているからです。
たとえば,「せいかん」という単語と,「せいけい」という単語は,「せいかん」の方が前にありますよね。これは,最初の2文字「せい」までは一緒ですが,3文字目の「か」と「け」は「か」の方が前にあるので,「せいかん」が前に来るわけです。
例2.
集合 X=\{x, y\} の部分集合全体の集合(べき集合) 2^X =\bigl\{\emptyset, \{x\}, \{y\}, \{x,y\}\bigr\} 上の,包含関係による順序 A\le B\xLeftrightarrow{\mathrm{def}} A\subset B を考えると,これは半順序集合である。このとき, 2^X\times 2^X 上の辞書式順序について,
(\{x\}, \{y\})\le (\{x,y\}, \emptyset)\le (\{x,y\}, \{y\})
であるが, (\{ x\}, \{x\}) と (\{x\}, \{y\}) の順序は定まらない。
半順序集合の場合は,辞書式順序も半順序集合になり,順序が定まらない2元もあります。
整列集合で添え字付けられた直積による辞書式順序
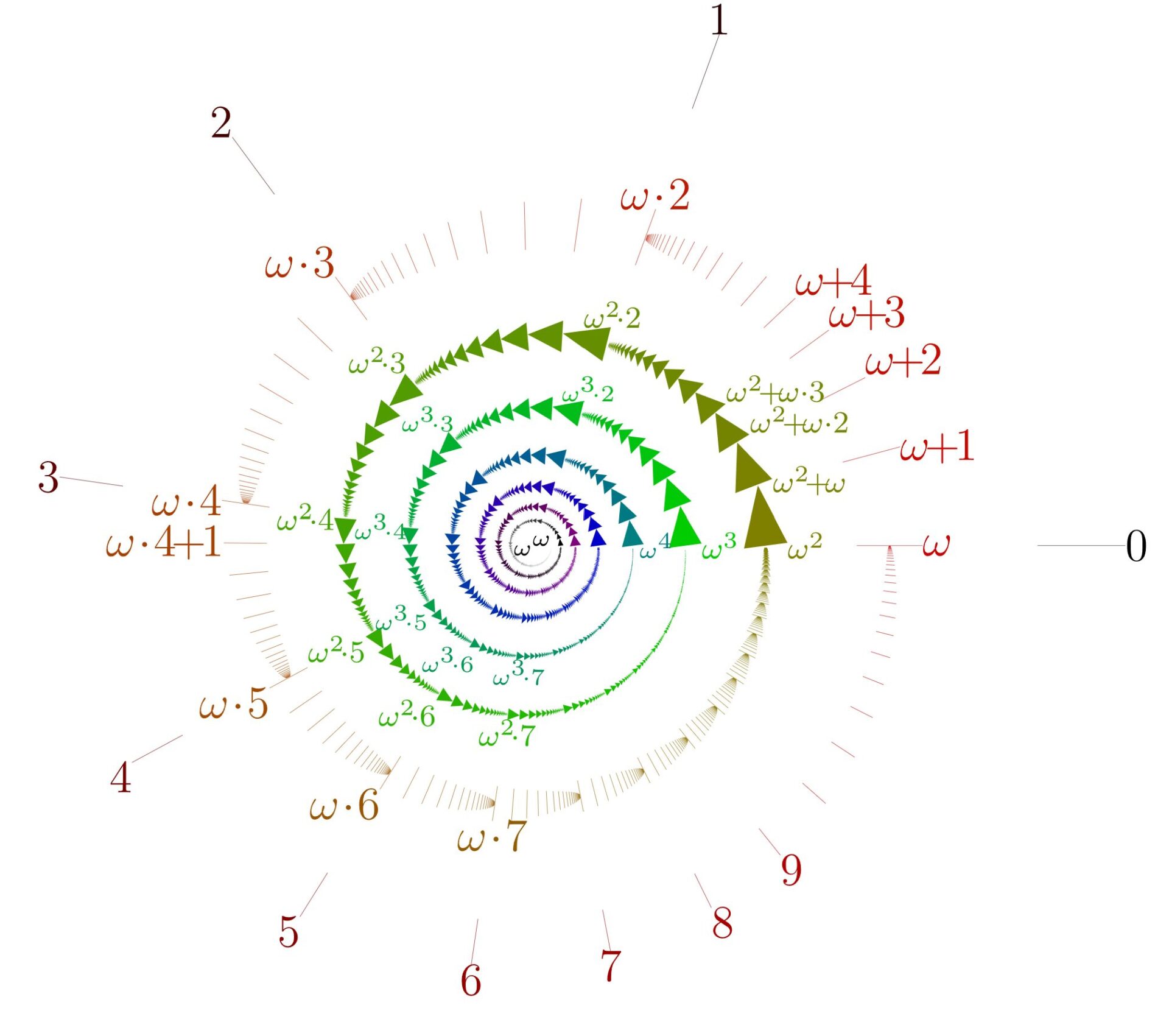
辞書式順序の定義をより一般化しておきましょう。整列集合とは,全順序集合でかつ任意の空でない部分集合が最小元をもつような集合を言います。たとえば,正の整数全体の集合は整列集合ですが,整数全体の集合や正の実数全体の集合は整列集合ではありません(→整列集合と整列可能定理)。
定義2(整列集合で添え字付けられた直積による辞書式順序)
I を整列集合とし,各 i\in I に対し,半順序集合(resp. 全順序集合) (A_i,\le ) が定まっているとする。このとき,直積集合 A =\prod_{i\in I} A_i 上の2元 (a_i)_i, (b_i)_i に対し,
\begin{aligned}&(a_i)_i< (b_i)_i \\ &\xLeftrightarrow{\mathrm{def}} a_j<b_j \;\; ( j = \min \{i\in I\mid a_i\ne b_i\})\end{aligned}
と定めると, (A, \le) は半順序集合 (resp. 全順序集合)になる。これを, A における辞書式順序 (lexicographical order, dictionary order) という。
a_i=b_i が成り立たない最小の添え字を考えて,その添え字が a_j \gtrless b_j かどうかで (a_i)_i と (b_i)_i の大小を決めているわけですね。半順序集合の場合は, a_j, b_j の大小が付けられないときがありますが,その場合は, (a_i)_i, (b_i)_i の大小も付けられないと考えます。
整列集合と辞書式順序
整列集合と辞書式順序にまつわる定理を紹介しておきましょう。
定理(整列集合の辞書式順序)
(A_1, \le), (A_2, \le),\ldots, (A_n, \le) を整列集合としたとき,直積集合 A=A_1\times A_2\times \cdots\times A_n も整列集合である。
そんなに難しくないですが,前半の証明をしましょう。1\le k\le n に対し, p_k \colon A\to A_k を自然な射影 (a_1, \ldots, a_n)\mapsto a_k とします。任意の空でない部分集合 B\subset A に最小元が存在することを示しましょう。
p_1(B)\subset A_1 は, A_1 が整列集合なので,最小元 m_1\in p_1(B) をもちます。 B_1=\{ (b_1, \ldots, b_n)\in B\mid b_1=m_1\} とすると,\emptyset \ne B_1\subset B です。つづいて, p_2(B_1)\subset A_2 は A_2 が整列集合なので,最小元 m_2\in p_2(B_1) をもちます。 B_2=\{ (b_1, \ldots, b_n)\in B_1 \mid b_2=m_2\} とすると, \emptyset \ne B_2\subset B_1 です。
同じ作業を同様に繰り返すことで, B の最小元 (m_1, \ldots, m_n) が見つかります。これで証明終わりです。要するに,全ての元から1番目の要素が最小のものを全部拾ってきて,拾ってきた中から,2番目の要素が最小のものを全部拾ってきて,拾ってきた中から……をn番目まで繰り返しているわけです。
つづいて,無限個の直積の辞書式順序では,整列集合になるとは限らないことを示しましょう。
A=\{0,1\}^\mathbb{N}=\prod_{i=1}^\infty \{0,1\}
として,部分集合 B\subset A を,
すなわち a_i=1 となる i\in \mathbb{N} が唯一つしかない (a_i)_i 全体の集合とします。このとき, B は最小元が存在しません。実際,
ですね。よって, A は整列集合ではありません。全順序集合ではあります。