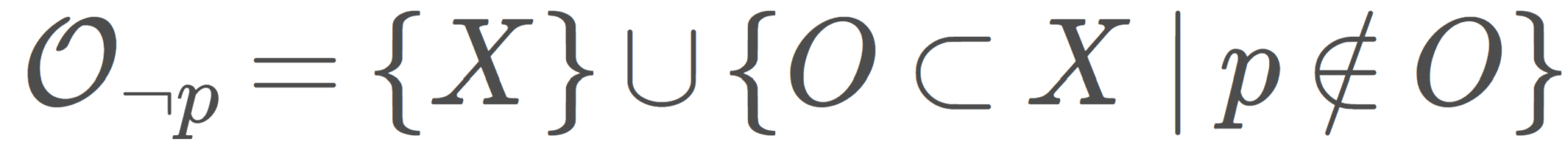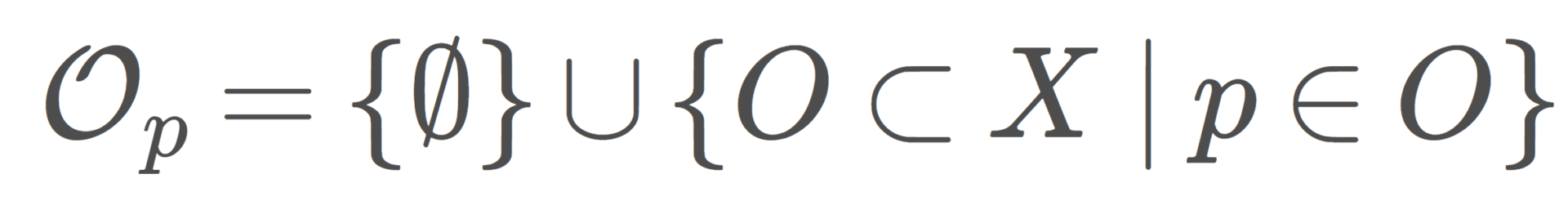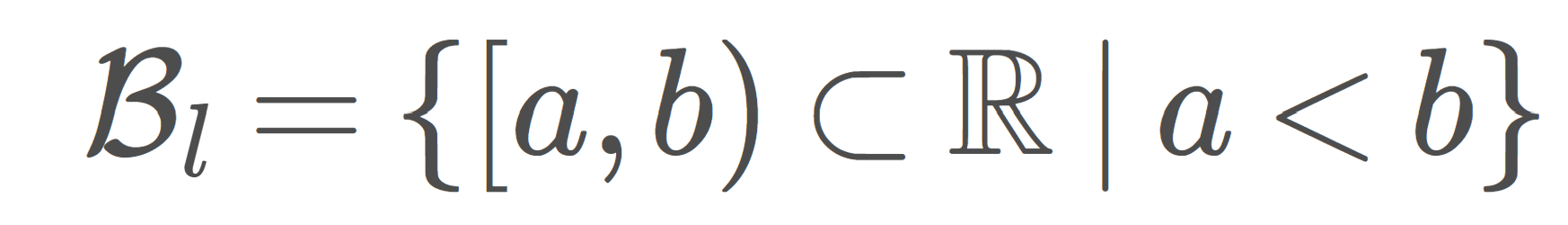除外点位相とは，ある特定の点 p を含まない部分集合全体を開集合系にするような位相空間で， T_0,T_4, T_5 分離公理をみたすが， T_1,T_2, T_3 をみたさない特殊な空間です。
除外点位相の定義と性質を掘り下げましょう。
除外点位相の定義
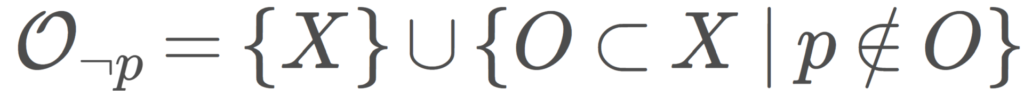
定義（除外点位相）
X を空でない集合とし， p\in X とする。
\Large \color{red}\mathcal{O}_{\neg p} =\{X\}\cup \{ O\subset X\mid p\notin O\}
を， p を含まない部分集合全体の集合（と全体集合の和集合）とすると，(X,\mathcal{O}_{\neg p}) は位相空間となる。この位相を除外点位相 (excluded point topology) という。
除外点位相の性質
可算性・分離性・コンパクト性・連結性に分けて性質を解説しますが，最初に紹介するもの全てまとめておきます。
| X の濃度 | 2点 (シェルピンスキー空間) | 3点以上の有限集合 可算集合 | 非可算集合 |
|---|---|---|---|
| 第一可算 | 〇 | 〇 | 〇 |
| 第二可算 | 〇 | 〇 | × |
| 可分 | 〇 | 〇 | × |
| T_0 空間 | 〇 | 〇 | 〇 |
| T_1, T_2, T_3 空間 | × | × | × |
| T_4, T_5 空間 | 〇 | 〇 | 〇 |
| コンパクト | 〇 | 〇 | 〇 |
| 点列コンパクト | 〇 | 〇 | 〇 |
| 連結 | 〇 | 〇 | 〇 |
| 弧状連結 | 〇 | 〇 | 〇 |
| 弧連結 | × | × | × |
| hyperconnected | 〇 | × | × |
| ultraconnected | 〇 | 〇 | 〇 |
順番に考えます。
1. 除外点位相と可算公理
定理1（除外点位相と可算公理）
(X,\mathcal{O}_{\neg p}) を除外点位相が入った位相空間とする。このとき，
定理1の証明
1.について，各点 x\in X\setminus\{p\} に対し， \mathcal{B}_x=\bigl\{\{x\}\bigr\} は x の基本近傍系である。また， \mathcal{B}_p=\{X\} は p の基本近傍系である。よって， X は第一可算である。
2.について，
\mathcal{B}= \{X\}\cup \bigl\{ \{x\}\mid x\in X\setminus \{p\} \bigr\}
とすると，これは (X,\mathcal{O}_{\neg p}) の開基であり，逆にすべての開基は \mathcal{B} を含む。よって， X が高々可算なら第二可算であるし，非可算なら第二可算でない。
3.について， A\subset X に対し，
\overline{A} = \begin{cases} A & p\in A \\ A\cup \{p\} & p\notin A\end{cases}
であるから， X が高々可算のとき可分だし，非可算のときは可分でない。
証明終
2. 除外点位相と分離公理
定理2（除外点位相と分離公理）
(X,\mathcal{O}_{\neg p}) を除外点位相が入った位相空間とする。このとき，
- X は T_0 空間である。
- X は T_1,T_2,T_3 空間でない。
- X は T_4, T_5 空間である。
本記事では， T_0 から T_5 は以下のように定義しています。この定義は文献によって変わりますから，注意してください。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ空間 (Kolmogorov space) | 任意の異なる2点 x,y\in X に対して， x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して， x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ空間 (Hausdorff space) | 任意の異なる2点 x,y\in X に対して， x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F に対して， F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| T_4 | 任意の2つの互いに素な空でない閉集合 F,G\subset X に対して， F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの空でない集合 A,B\subset X に対して， A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
定理2の証明
1.について， x,y\in X を異なる2点とすると，少なくとも一方は p とは異なるので， x\ne p とする。このとき， \{x\} は， x は含むが y は含まない開集合なので， T_0 分離公理をみたす。
2.について， p を含む開集合は X しかないので， p を含むが， x\in X\setminus\{p\} を含まない開集合は存在しない。よって，T_1 空間でない。これより， T_2 空間でもない。また，空でない閉集合 F は p を必ず含むので， F を含む開集合は X しかない。したがって， T_3 空間でもない。
3.について示す。空でない閉集合は，必ず p を含むので，空でない2つの閉集合 F,G\subset X は取れない。よって， T_4 空間である(空虚な真)。
また，空でない A,B\subset X を， \overline{A}\cap B=\emptyset をみたすとする。\overline{A} は p を含むから， p\notin B である。また， A\cap \overline{B}=\emptyset もみたすとすると，同様に p\notin A となる。このとき， A, B 自身が互いに素な開集合である。ゆえに T_5 空間である。
証明終
3. 除外点位相とコンパクト性
定理3の証明
1.について， \{U_\lambda\}\subset \mathcal{O}_{\neg p} を X の開被覆とすると， p を含むある開集合 U_\lambda\in \mathcal{O}_{\neg p} が存在するが， p を含む開集合は X のみなので， U_\lambda =X でなければならない。よって， \{X\} は部分被覆となるので，コンパクトである。
2.について， \{x_n\}\subset X を任意の点列すると， p を含む開集合は X のみなので，この点列は p に収束する。ゆえに，点列コンパクトである。
証明終
4. 除外点位相と連結性
定理4（除外点位相と連結性）
(X,\mathcal{O}_{\neg p}) を除外点位相が入った位相空間とする。このとき，
- X は連結である。
- X は弧状連結である。
- X は弧連結でない。
- X は2点集合(シェルピンスキー空間)のとき，hyperconnected であり，3点以上の集合のときは hyperconnected でない。
- X は ultraconnected である。
まず定義を確認しておきましょう。
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な開集合 U,V で， U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について，ある連続写像 f\colon [0,1]\to X で， f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として，埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる（※単に全単射なものが取れるとすることもある。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値） |
| hyperconnected | 任意の空でない2つの開集合が常に共通部分を持つ |
| ultraconnected | 任意の空でない2つの閉集合が常に共通部分を持つ |
定理4の証明
1,2,5.について
任意の空でない閉集合は p を含むので，ultraconnected である。ultraconnected なら弧状連結だし，弧状連結なら連結なので，1,2,5.が示せた。
4.はほぼ明らかなので略。
3.について
f\colon [0,1]\to X を全単射かつ連続とする。 x\in f([0,1])\setminus \{p\} とすると， \{x\} は開集合なので， f^{-1}(\{x\})\subset [0,1] も開集合であるが， f は全単射なので1点集合でもある。これはあり得ない。ゆえに弧連結でない。
証明終
関連する記事
除外点位相 (X,\mathcal{O}_{\neg p}) の閉集合族
\mathcal{F}=\{\emptyset\}\cup \{ F\subset X\mid p\in F\}
は， p を含む部分集合全体（と空集合）のことを指します。\mathcal{F} はまた開集合族の定義をみたしており，位相空間 (X,\mathcal{F}) を考えることができます。これを特定点位相 (particular point topology) といいます。除外点位相とは，異なった性質をもちます。以下で解説しています。
その他の関連記事を挙げます。
