幾何分布のモーメント母関数・特性関数とその導出証明

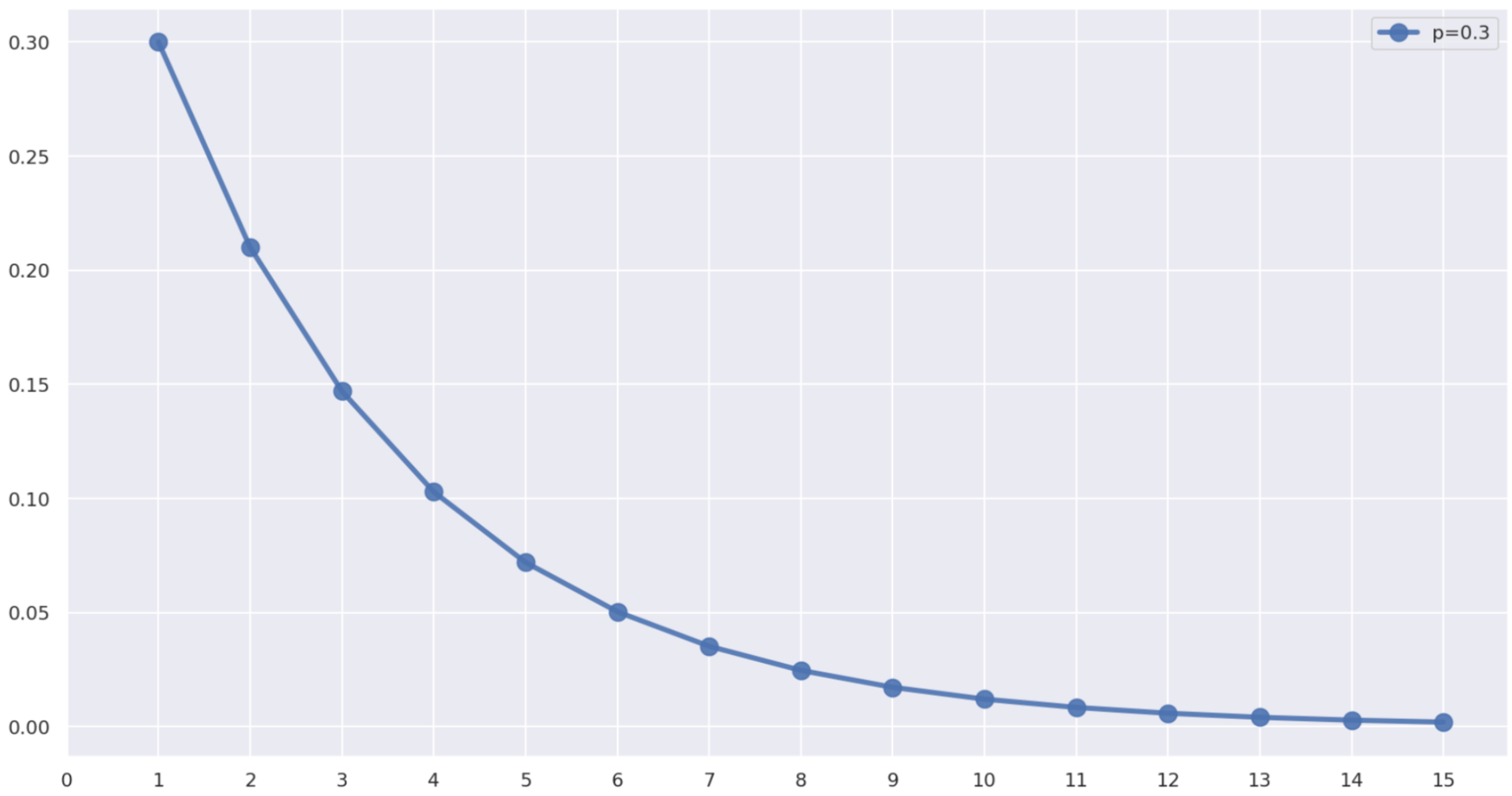
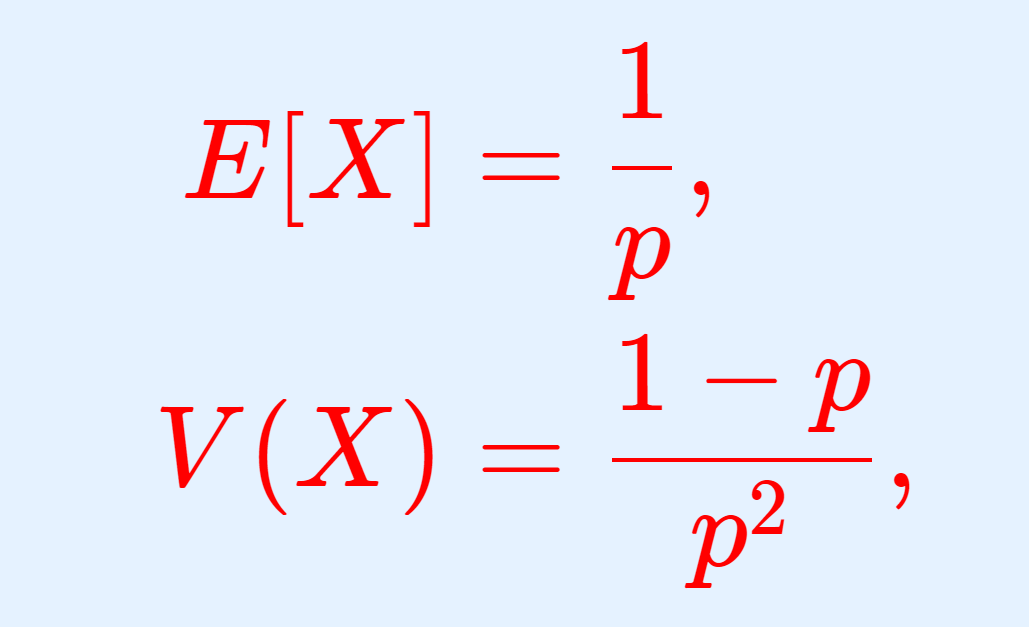幾何分布は，コインで初めて表が出る試行回数を表す離散型確率分布です。これについて，そのモーメント母関数(積率母関数)・特性関数は

\begin{aligned} E[e^{tX}] &=\dfrac{pe^{t}}{1-(1-p)e^t}, \quad t< -\log(1-p), \\ E[e^{itX}]&= \dfrac{pe^{it}}{1-(1-p)e^{it}}, \quad t\in\mathbb{R} \end{aligned}

となります。これについて，その証明をしましょう。

幾何分布のモーメント母関数(積率母関数)・特性関数

まずは，もう一度ちゃんとモーメント母関数(積率母関数)・特性関数がどうなるか述べましょう。

定理（幾何分布の積率母関数・特性関数）

$X \sim \operatorname{Geo}(p)$ とする。このとき，幾何分布の積率母関数(モーメント母関数)・特性関数はそれぞれ

\color{red}\begin{aligned} E[e^{tX}] &=\dfrac{pe^{t}}{1-(1-p)e^t}, \quad t< -\log(1-p), \\ E[e^{itX}]&= \dfrac{pe^{it}}{1-(1-p)e^{it}}, \quad t\in\mathbb{R} \end{aligned}

である。

証明に行く前に，まず，幾何分布の定義を復習しておきましょう。

幾何分布の定義

$X$ を確率変数， $0<p<1$ とする。 $k=1,2,3,\ldots$ に対し，

\color{red} P(X=k) = (1-p)^{k-1} p

が成立するとき， $X$ はパラメータ $p$ の幾何分布 (geometric distribution) に従うという。本記事では，これを $\color{red} X\sim \operatorname{Geo}(p)$ とかくことにする。

幾何分布は，離散型確率分布の1つで，「確率 $p$ で表が出るコインを何回も振ったときに，何回目に初めて表が出るか」をモデル化したものです。幾何分布について，詳しくは以下の記事を参照してください。

を順番にやっていきましょう。

証明

\begin{aligned} E[e^{tX}]&= \sum_{k=1}^\infty e^{tk} P(X=k) \\ &= \sum_{k=1}^\infty e^{tk} (1-p)^{k-1} p \\ &= pe^t \sum_{k=1}^\infty ((1-p)e^t)^{k-1} \end{aligned}

であるから，等比級数の和を求めるとよい。和は $(1-p)e^t< 1$ すなわち $t<-\log (1-p)$ のとき収束して，

\begin{aligned} pe^t \sum_{k=1}^\infty ((1-p)e^t)^{k-1} &= pe^t \frac{1}{1-(1-p)e^t} \\ &=\frac{pe^t}{1-(1-p)e^t} \end{aligned}

となるから， $E[e^{tX}] =\dfrac{pe^{t}}{1-(1-p)e^t}, \quad t< -\log(1-p)$ を得る。

証明終

「無限等比級数」に帰着させることで，証明することができましたね。

特性関数の導出も，積率母関数とほぼ同じですが，確認していきましょう。

証明

\begin{aligned} E[e^{itX}]&= \sum_{k=1}^\infty e^{itk} P(X=k) \\ &= \sum_{k=1}^\infty e^{itk} (1-p)^{k-1} p \\ &= pe^{it} \sum_{k=1}^\infty ((1-p)e^{it})^{k-1} \end{aligned}

であるから，等比級数の和を求めるとよい。和は $|(1-p)e^{it}|< 1$ であるから，収束して，

\begin{aligned} pe^{it} \sum_{k=1}^\infty ((1-p)e^{it})^{k-1} &= pe^{it} \frac{1}{1-(1-p)e^{it}} \\ &=\frac{pe^{it}}{1-(1-p)e^{it}} \end{aligned}

となるから， $E[e^{itX}] =\dfrac{pe^{it}}{1-(1-p)e^{it}}$ を得る。

証明終