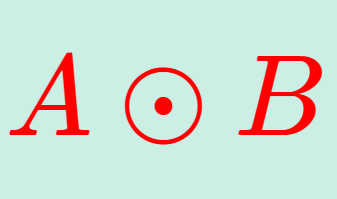【アダマール積】行列の要素ごとの積

「行列の積」というと，難しい定義のものが一般的ですが，行列の要素・成分ごとの積であるアダマール積について紹介します。

アダマール積ではなく，普通の行列の積について知りたい場合は，以下の記事を参照してください。

行列のアダマール積の定義
アダマール積の具体例
アダマール積の性質

行列のアダマール積の定義

定義（アダマール積）

$A = (a_{ij}) , B = (b_{ij})$ を $m \times n$ 行列とする。このとき，そのアダマール積 (Hadamard product) $\color{red}C = A \odot B$ (または $\color{red}C = A \circ B$ ), $C=(c_{ij})$ を

\color{red} c_{ij} = a_{ij} b_{ij}

で定義する。すなわち，

\color{red}\scriptsize \begin{aligned} &\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} \odot \begin{pmatrix} b_{11} & b_{12} & \ldots & b_{1n} \\ b_{21} & b_{22} & \ldots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \ldots & b_{mn} \end{pmatrix} \\ &= \begin{pmatrix} a_{11} b_{11} & a_{12} b_{12}& \ldots & a_{1n} b_{1n} \\ a_{21} b_{21} & a_{22} b_{22} & \ldots & a_{2n} b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} b_{m1} & a_{m2} b_{m2} & \ldots & a_{mn} b_{mn} \end{pmatrix}\end{aligned}

と定義する。

こちらの方が，積としては自然と感じるかもしれません。ポイントは以下です。

Point～アダマール積～

アダマール積は同じ形の行列に対して定義され，同じ形の行列を返す。

具体例を挙げましょう。

アダマール積の具体例

アダマール積の具体例

$\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \odot \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 6 \end{pmatrix}.$
$\begin{pmatrix} 1 & 2\\ 3 & 4 \end{pmatrix} \odot \begin{pmatrix} 3 & 0 \\ 1 & -1 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 3 & -4 \end{pmatrix} .$